Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product.The zero matrix is the only matrix whose rank is 0.The rank of a Matrix Definition
The rank of the matrix is the dimension of the vector space obtained by its columns. The rank of a matrix cannot exceed more than the number of its rows or columns. The rank of the null matrix is zero.
What is the determinant of a rank 1 matrix : What is the determinant of a rank-one matrix – Quora. This question is rather strange, but the answer is very simple : if A is a square matrix of order n and Rank A = r , 1 < r < n then | A | = 0 ; if r = n then | A | ≠ 0 .
What does a 1 mean for matrix
If we consider a matrix A, we denote its inverse as A-1. The inverse of a matrix is another matrix that, when multiplied by the given matrix, yields the multiplicative identity. For a matrix A, its inverse is A-1. And A.A-1 = I, where I is denoted as the identity matrix.
Can a 3×3 matrix have a rank of 1 : Theorem: The Rank of a 3 × 3 Matrix with Three Scalar Multiple Rows/Columns. A 3 × 3 matrix 𝐴 , where 𝐴 ≠ 0 × , has rank R K ( 𝐴 ) = 1 if and only if it contains three rows/columns that are scalar multiples of each other.
The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 . This happens because two basis vectors are merged in the same vector in the output, so one dimension is bound to collapse. instead of 3. In fact, it is common intuition that when the rank is not full, some dimensions are lost in the transformation. Even if it's a 3×3 matrix, the output only has 2 dimensions.
What makes a matrix full rank
A matrix is said to have full rank if its rank equals the largest possible for a matrix of the same dimensions, which is the lesser of the number of rows and columns. A matrix is said to be rank-deficient if it does not have full rank.Sure, you can have a matrix of rank 4, or 5 or 6 or any higher integer. It's just you need longer vectors, spaces of higher dimension than 3 (indeed the Cliff's notes explicitly state 3-vectors).The determinant of a permutation matrix P is 1 or −1 depending on whether P exchanges an even or odd number of rows. From these three properties we can deduce many others: 4. If two rows of a matrix are equal, its determinant is zero. Since a zero determinant of any n x n matrix implies that the rank must be less than n, the rank for a 2×2 matrix must be 0 (null matrix) or 1. As a standard exercise in linear algebra, we can show that any rank-1 matrix may be written as the outer product of two vectors, a well-documented result in textbooks.
What is a 1 in matrix : The inverse of a square matrix A, denoted by A-1, is the matrix so that the product of A and A-1 is the identity matrix. The identity matrix that results will be the same size as matrix A.
Can a 3×3 matrix have rank 2 : Theorem: The Rank of a 3 × 3 Matrix with Two Scalar Multiple Rows/Columns. If a 3 × 3 matrix 𝐴 , containing no zero rows/columns, contains two rows/columns that are scalar multiples of each other and a third row/column that is not a scalar multiple of the other two, then R K ( 𝐴 ) = 2 .
Does 0 technically exist
0 (zero) is a number representing an empty quantity. Adding 0 to any number leaves that number unchanged. In mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and complex numbers, as well as other algebraic structures. Immortal: What is Immortal rank in Valorant Immortal is the second highest rank anyone can get and, just like every rank below it, is divided up into three tiers.The rank of an m × n matrix is a nonnegative integer and cannot be greater than either m or n. That is, A matrix that has rank min(m, n) is said to have full rank; otherwise, the matrix is rank deficient. Only a zero matrix has rank zero.
Can a 3×3 matrix have rank 3 : The rank of a matrix is equal to the number of linearly independent rows (or columns) in it. Hence, it cannot more than its number of rows and columns. For example, if we consider the identity matrix of order 3 × 3, all its rows (or columns) are linearly independent and hence its rank is 3.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Why is matrix rank 1? Weitere Antworten – What does it mean if a matrix is rank 1
Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product.The zero matrix is the only matrix whose rank is 0.The rank of a Matrix Definition
The rank of the matrix is the dimension of the vector space obtained by its columns. The rank of a matrix cannot exceed more than the number of its rows or columns. The rank of the null matrix is zero.
What is the determinant of a rank 1 matrix : What is the determinant of a rank-one matrix – Quora. This question is rather strange, but the answer is very simple : if A is a square matrix of order n and Rank A = r , 1 < r < n then | A | = 0 ; if r = n then | A | ≠ 0 .
What does a 1 mean for matrix
If we consider a matrix A, we denote its inverse as A-1. The inverse of a matrix is another matrix that, when multiplied by the given matrix, yields the multiplicative identity. For a matrix A, its inverse is A-1. And A.A-1 = I, where I is denoted as the identity matrix.
Can a 3×3 matrix have a rank of 1 : Theorem: The Rank of a 3 × 3 Matrix with Three Scalar Multiple Rows/Columns. A 3 × 3 matrix 𝐴 , where 𝐴 ≠ 0 × , has rank R K ( 𝐴 ) = 1 if and only if it contains three rows/columns that are scalar multiples of each other.
The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 .
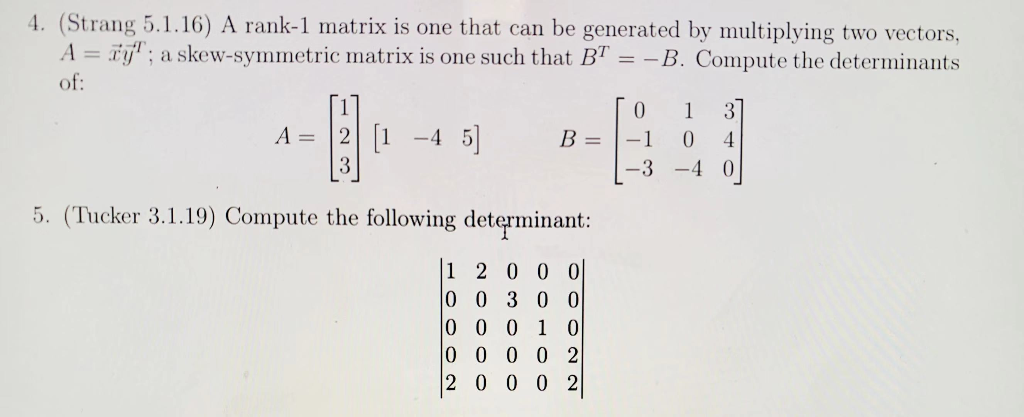
This happens because two basis vectors are merged in the same vector in the output, so one dimension is bound to collapse. instead of 3. In fact, it is common intuition that when the rank is not full, some dimensions are lost in the transformation. Even if it's a 3×3 matrix, the output only has 2 dimensions.
What makes a matrix full rank
A matrix is said to have full rank if its rank equals the largest possible for a matrix of the same dimensions, which is the lesser of the number of rows and columns. A matrix is said to be rank-deficient if it does not have full rank.Sure, you can have a matrix of rank 4, or 5 or 6 or any higher integer. It's just you need longer vectors, spaces of higher dimension than 3 (indeed the Cliff's notes explicitly state 3-vectors).The determinant of a permutation matrix P is 1 or −1 depending on whether P exchanges an even or odd number of rows. From these three properties we can deduce many others: 4. If two rows of a matrix are equal, its determinant is zero.
Since a zero determinant of any n x n matrix implies that the rank must be less than n, the rank for a 2×2 matrix must be 0 (null matrix) or 1. As a standard exercise in linear algebra, we can show that any rank-1 matrix may be written as the outer product of two vectors, a well-documented result in textbooks.
What is a 1 in matrix : The inverse of a square matrix A, denoted by A-1, is the matrix so that the product of A and A-1 is the identity matrix. The identity matrix that results will be the same size as matrix A.
Can a 3×3 matrix have rank 2 : Theorem: The Rank of a 3 × 3 Matrix with Two Scalar Multiple Rows/Columns. If a 3 × 3 matrix 𝐴 , containing no zero rows/columns, contains two rows/columns that are scalar multiples of each other and a third row/column that is not a scalar multiple of the other two, then R K ( 𝐴 ) = 2 .
Does 0 technically exist
0 (zero) is a number representing an empty quantity. Adding 0 to any number leaves that number unchanged. In mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and complex numbers, as well as other algebraic structures.
Immortal: What is Immortal rank in Valorant Immortal is the second highest rank anyone can get and, just like every rank below it, is divided up into three tiers.The rank of an m × n matrix is a nonnegative integer and cannot be greater than either m or n. That is, A matrix that has rank min(m, n) is said to have full rank; otherwise, the matrix is rank deficient. Only a zero matrix has rank zero.
Can a 3×3 matrix have rank 3 : The rank of a matrix is equal to the number of linearly independent rows (or columns) in it. Hence, it cannot more than its number of rows and columns. For example, if we consider the identity matrix of order 3 × 3, all its rows (or columns) are linearly independent and hence its rank is 3.