So, a positive slope means the function is increasing while a negative slope means the function is decreasing. Increasing functions have y-values that increase as x-values increase, whereas decreasing functions have y-values that decrease while x-values increase.Making the input and the output of a function negative results in a rotation of the function around the origin. Here is a graph of y = f (x) and y = – f (- x). Note that if (x, y) is a point on the graph of f (x), then (- x, – y) is a point on the graph of – f (- x).Given the graph of y equals f of x. Below which of the following might be f of x. It is clear that negative 4 1 negative 2 0 and 0 1 are points on the graph.
How do you flip a negative graph : And it's u-shaped that's a parabola. And so what I want to do is I want you to take that function. And multiply by a negative on the outside.
What determines if a graph is positive or negative
If the graph of a line rises from left to right, the slope is positive. If the graph of the line falls from left to right the slope is negative.
How to tell if a graph is negative or positive : If the graph of a line rises from left to right, the slope is positive. If the graph of the line falls from left to right the slope is negative.
We want to talk about where this function is positive. So the function is positive when my Y values are greater than 0. So this remember represents my Y axis. And my Y axis is positive above the x The equation y = f(x) represents a functional relationship between a dependent variable (y) and one or more independent variables (x). In mathematical terms, it describes how changes in the independent variables (x) lead to changes in the dependent variable (y).
What does FX K do to a graph
Transformations of Function Graphs
Notation
Changes to f (x)
Coordinate Change
f (-x)
reflection over the y-axis
(x, y) → (-x, y)
f (x) + k
vertical shift up k units
(x, y) → (x, y + k)
f (x) – k
vertical shift down k units
(x, y) → (x, y – k)
To reflect the graph of a function h(x) over the x-axis (that is, to flip the graph upside-down), multiply the function by −1 to get −h(x). To reflect the graph of a function h(x) around the y-axis (that is, to mirror the two halves of the graph), multiply the argument of the function by −1 to get h(−x).The inverse function swaps the x and y values of the original function, and the graph of this inverse function is a reflection of the original function about the line y=x. The graph of a negative slope moves downwards from left to right. When looking at a graph on an xy coordinate plane, as x increases, y decreases, making it a negative slope.
Is 0 positive or negative : neither positive nor negative
Zero is neither positive nor negative. It is the only number with such characteristics. The numbers to the right of zero on the number line are positive and those on the left side are negative. Q.
Is f(- 4 positive or negative : Interval: 1 < x < ∞
Interval
The value of a specific within the interval
Sign of on interval
− ∞ < x < − 3
f ( − 4 ) < 0
negative
− 3 < x < 1
f ( 0 ) > 0
positive
1 < x < ∞
f ( 2 ) > 0
positive
What makes negative and positive
Positive numbers are those which are greater than zero. Negative numbers are those which are less than zero. Below is a table to help you remember what to do with the sign when using multiplication or division and addition or subtraction. A function f from X to Y is an object that, for each element x ∈ X, assigns an element y ∈ Y . We use the notation f : X → Y to denote a function as described. We write f(x) = y or f : x ↦→ y to denote that the element in Y assigned to x is y. We call X the domain of f, and we call Y the codomain of f.If y is expressed in terms of a variable x as y=f(x), then y is called. Linear function.
How does H and K affect a graph : In this equation, h represents the horizontal shift, or how far the graph moves horizontally from x=0, and k represents the vertical shift, or how far the graph moves vertically from y=0, and a is a constant that tells us how much the graph stretches or shrinks vertically and if the a is negative, it tells us that the …
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort What makes a graph flip? Weitere Antworten – How does a graph change when it’s negative
So, a positive slope means the function is increasing while a negative slope means the function is decreasing. Increasing functions have y-values that increase as x-values increase, whereas decreasing functions have y-values that decrease while x-values increase.Making the input and the output of a function negative results in a rotation of the function around the origin. Here is a graph of y = f (x) and y = – f (- x). Note that if (x, y) is a point on the graph of f (x), then (- x, – y) is a point on the graph of – f (- x).Given the graph of y equals f of x. Below which of the following might be f of x. It is clear that negative 4 1 negative 2 0 and 0 1 are points on the graph.
How do you flip a negative graph : And it's u-shaped that's a parabola. And so what I want to do is I want you to take that function. And multiply by a negative on the outside.
What determines if a graph is positive or negative
If the graph of a line rises from left to right, the slope is positive. If the graph of the line falls from left to right the slope is negative.
How to tell if a graph is negative or positive : If the graph of a line rises from left to right, the slope is positive. If the graph of the line falls from left to right the slope is negative.
We want to talk about where this function is positive. So the function is positive when my Y values are greater than 0. So this remember represents my Y axis. And my Y axis is positive above the x
The equation y = f(x) represents a functional relationship between a dependent variable (y) and one or more independent variables (x). In mathematical terms, it describes how changes in the independent variables (x) lead to changes in the dependent variable (y).
What does FX K do to a graph
To reflect the graph of a function h(x) over the x-axis (that is, to flip the graph upside-down), multiply the function by −1 to get −h(x). To reflect the graph of a function h(x) around the y-axis (that is, to mirror the two halves of the graph), multiply the argument of the function by −1 to get h(−x).The inverse function swaps the x and y values of the original function, and the graph of this inverse function is a reflection of the original function about the line y=x.
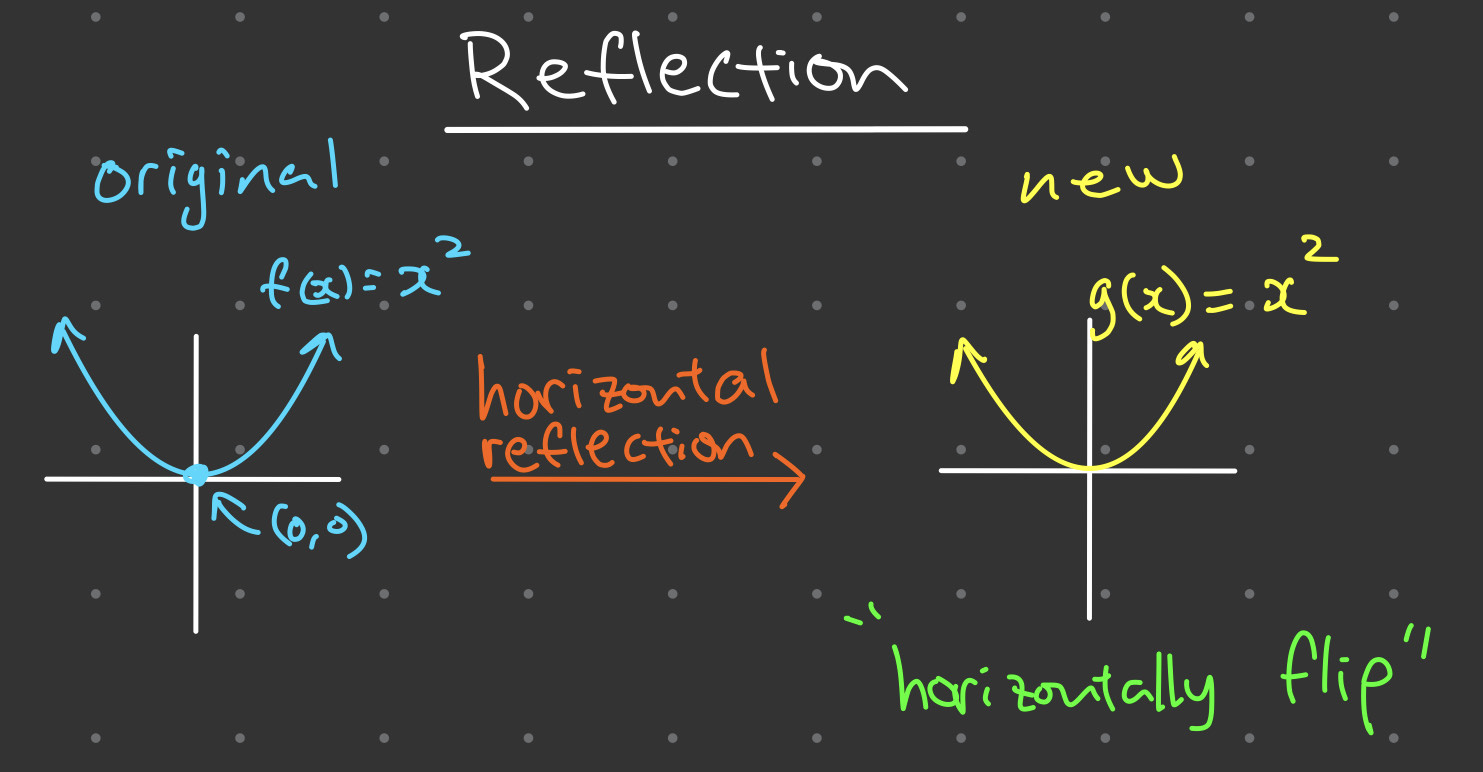
The graph of a negative slope moves downwards from left to right. When looking at a graph on an xy coordinate plane, as x increases, y decreases, making it a negative slope.
Is 0 positive or negative : neither positive nor negative
Zero is neither positive nor negative. It is the only number with such characteristics. The numbers to the right of zero on the number line are positive and those on the left side are negative. Q.
Is f(- 4 positive or negative : Interval: 1 < x < ∞
What makes negative and positive
Positive numbers are those which are greater than zero. Negative numbers are those which are less than zero. Below is a table to help you remember what to do with the sign when using multiplication or division and addition or subtraction.
A function f from X to Y is an object that, for each element x ∈ X, assigns an element y ∈ Y . We use the notation f : X → Y to denote a function as described. We write f(x) = y or f : x ↦→ y to denote that the element in Y assigned to x is y. We call X the domain of f, and we call Y the codomain of f.If y is expressed in terms of a variable x as y=f(x), then y is called. Linear function.
How does H and K affect a graph : In this equation, h represents the horizontal shift, or how far the graph moves horizontally from x=0, and k represents the vertical shift, or how far the graph moves vertically from y=0, and a is a constant that tells us how much the graph stretches or shrinks vertically and if the a is negative, it tells us that the …