Any linear combination of zero vectors is again a zero vector. The space containing only the zero vector and no others is considered to be zero-dimensional. The rank is then zero.A vector is an element in a vector space. As such, it has no rank. A matrix, in the context of linear algebra, is interesting because it represents a linear transformation between vector spaces.Properties of the Rank of the Matrix:
Zero matrices have no non-zero row. Hence it has an independent row (or column). So, the rank of the zero matrices is zero.
Do vectors have ranks : Ranking Vectors. Rank(v)—Returns a vector corresponding to the sorted positions of each element of vector v. The rank of the first entry is always 1.
What if a vector is 0
We define a vector as an object with a length and a direction. However, there is one important exception to vectors having a direction: the zero vector, i.e., the unique vector having zero length. With no length, the zero vector is not pointing in any particular direction, so it has an undefined direction.
What is the zero vector : A zero vector or a null vector is defined as a vector in space that has a magnitude equal to 0 and an undefined direction. Zero vector symbol is given by →0=(0,0,0) 0 → = ( 0 , 0 , 0 ) in three dimensional space and in a two-dimensional space, it written as →0=(0,0) 0 → = ( 0 , 0 ) .
The VECTOR RANK function returns a new vector that specifies the rank of the elements in vec. If direction is greater than 0 the entries are ranked from smallest to biggest, otherwise from biggest to smallest. The first ranked element has a rank of 1, the second of 2 and so on. If the vector is non-zero, this is obviously true. If the vector is zero (all its elements are 0), then the space it spans is reduced to itself only (multiplying the zero vector with any number always gives back the zero vector). So in this case only, it will not have full rank in the matrix sense.
What does rank 0 mean
For most items, a sales rank of zero simply means that the item has never sold, or has not sold in a long, long, long time. This will apply to most of the items that have no sales rank, but there are sometimes exceptions. Some categories don't offer up sales ranks for all items. Electronics is an example.With no length, the zero vector is not pointing in any particular direction, so it has an undefined direction. We denote the zero vector with a boldface 0, or if we can't do boldface, with an arrow →0. It behaves essentially like the number 0. If we add 0 to any vector a, we get the vector a back again unchanged.To get the first element of a vector, we could do the following. In R, array indexes start at 1 – the 1st element is at index 1. This is different than 0-based languages like C, Python, or Java where the first element is at index 0. A zero vector or a null vector is defined as a vector in space that has a magnitude equal to 0 and an undefined direction. Zero vector symbol is given by →0=(0,0,0) 0 → = ( 0 , 0 , 0 ) in three dimensional space and in a two-dimensional space, it written as →0=(0,0) 0 → = ( 0 , 0 ) .
Is 0 a magnitude : The zero vector (vector where all values are 0) has a magnitude of 0, but all other vectors have a positive magnitude.
Is the zero vector 0 unique : The two zero vectors are equal, which is a contraction to our assumption. Hence, the zero vector is unique. Therefore the given statement is true. Note: In vector space zero vector is always defined with respect to addition not with respect to multiplication.
Is a vector a rank 1 tensor
In fact tensors are merely a generalisation of scalars and vectors; a scalar is a zero rank tensor, and a vector is a first rank tensor. The rank (or order) of a tensor is defined by the number of directions (and hence the dimensionality of the array) required to describe it. A matrix is said to have full rank if its rank equals the largest possible for a matrix of the same dimensions, which is the lesser of the number of rows and columns. A matrix is said to be rank-deficient if it does not have full rank.The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 .
What is rank 0 tensor : Rank 0: A tensor with rank 0 is called a scalar. It represents a single value, such as a real number or a constant. Rank 1: A tensor with rank 1 is called a vector. Vectors have one-dimensional data and can be represented as a list of values.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort What is the rank of a zero vector? Weitere Antworten – What is the rank of the zero vector
Any linear combination of zero vectors is again a zero vector. The space containing only the zero vector and no others is considered to be zero-dimensional. The rank is then zero.A vector is an element in a vector space. As such, it has no rank. A matrix, in the context of linear algebra, is interesting because it represents a linear transformation between vector spaces.Properties of the Rank of the Matrix:
Zero matrices have no non-zero row. Hence it has an independent row (or column). So, the rank of the zero matrices is zero.
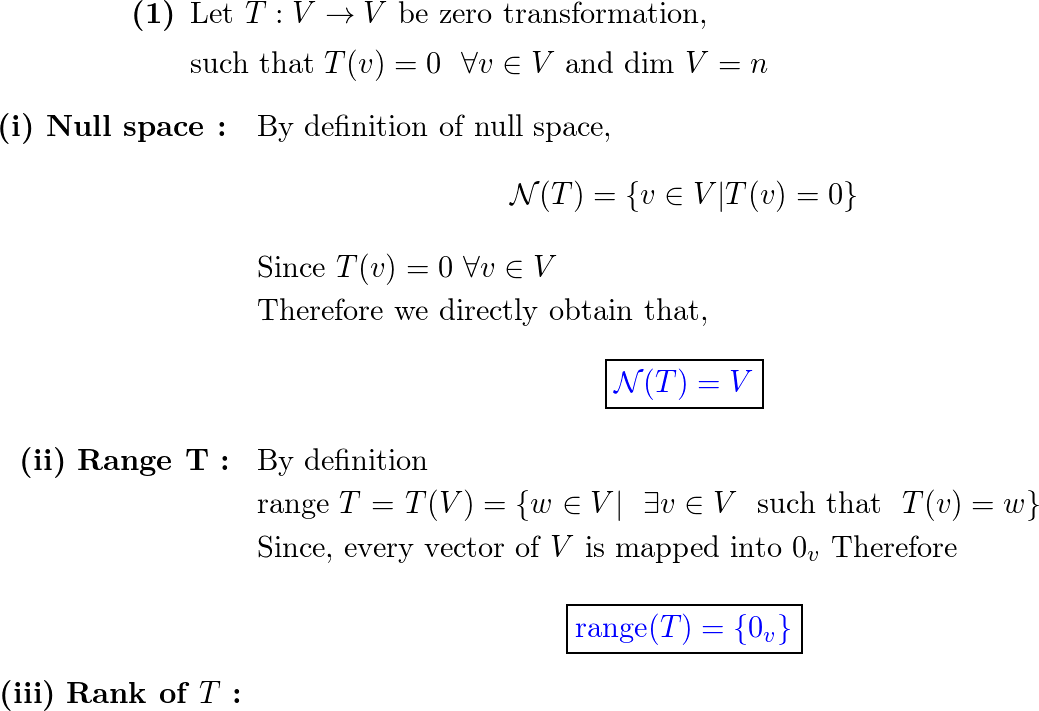
Do vectors have ranks : Ranking Vectors. Rank(v)—Returns a vector corresponding to the sorted positions of each element of vector v. The rank of the first entry is always 1.
What if a vector is 0
We define a vector as an object with a length and a direction. However, there is one important exception to vectors having a direction: the zero vector, i.e., the unique vector having zero length. With no length, the zero vector is not pointing in any particular direction, so it has an undefined direction.
What is the zero vector : A zero vector or a null vector is defined as a vector in space that has a magnitude equal to 0 and an undefined direction. Zero vector symbol is given by →0=(0,0,0) 0 → = ( 0 , 0 , 0 ) in three dimensional space and in a two-dimensional space, it written as →0=(0,0) 0 → = ( 0 , 0 ) .
The VECTOR RANK function returns a new vector that specifies the rank of the elements in vec. If direction is greater than 0 the entries are ranked from smallest to biggest, otherwise from biggest to smallest. The first ranked element has a rank of 1, the second of 2 and so on.
If the vector is non-zero, this is obviously true. If the vector is zero (all its elements are 0), then the space it spans is reduced to itself only (multiplying the zero vector with any number always gives back the zero vector). So in this case only, it will not have full rank in the matrix sense.
What does rank 0 mean
For most items, a sales rank of zero simply means that the item has never sold, or has not sold in a long, long, long time. This will apply to most of the items that have no sales rank, but there are sometimes exceptions. Some categories don't offer up sales ranks for all items. Electronics is an example.With no length, the zero vector is not pointing in any particular direction, so it has an undefined direction. We denote the zero vector with a boldface 0, or if we can't do boldface, with an arrow →0. It behaves essentially like the number 0. If we add 0 to any vector a, we get the vector a back again unchanged.To get the first element of a vector, we could do the following. In R, array indexes start at 1 – the 1st element is at index 1. This is different than 0-based languages like C, Python, or Java where the first element is at index 0.
A zero vector or a null vector is defined as a vector in space that has a magnitude equal to 0 and an undefined direction. Zero vector symbol is given by →0=(0,0,0) 0 → = ( 0 , 0 , 0 ) in three dimensional space and in a two-dimensional space, it written as →0=(0,0) 0 → = ( 0 , 0 ) .
Is 0 a magnitude : The zero vector (vector where all values are 0) has a magnitude of 0, but all other vectors have a positive magnitude.
Is the zero vector 0 unique : The two zero vectors are equal, which is a contraction to our assumption. Hence, the zero vector is unique. Therefore the given statement is true. Note: In vector space zero vector is always defined with respect to addition not with respect to multiplication.
Is a vector a rank 1 tensor
In fact tensors are merely a generalisation of scalars and vectors; a scalar is a zero rank tensor, and a vector is a first rank tensor. The rank (or order) of a tensor is defined by the number of directions (and hence the dimensionality of the array) required to describe it.
A matrix is said to have full rank if its rank equals the largest possible for a matrix of the same dimensions, which is the lesser of the number of rows and columns. A matrix is said to be rank-deficient if it does not have full rank.The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 .
What is rank 0 tensor : Rank 0: A tensor with rank 0 is called a scalar. It represents a single value, such as a real number or a constant. Rank 1: A tensor with rank 1 is called a vector. Vectors have one-dimensional data and can be represented as a list of values.