And then you're going to peel up a block of cards pivoting. It like you're a big block your index finger yeah yeah big block and that'll give you more cards to shuffle. With.Riffle seven times and you'll have a sufficiently random ordering of cards, an ordering that has likely never existed before. In other words, it's unlikely you'll ever shuffle two decks the same. The card shuffling result appears in a Numberphile video from 2015, along with a number of other card shuffling facts.We know from the Fun Fact Seven Shuffles that 7 random riffle shuffles are enough to make almost every configuration equally likely in a deck of 52 cards.
What is a perfect in shuffle of a deck of 52 cards : A perfect in-shuffle of a deck of 52 cards is defined as follows. The deck is cut in half followed by interleaving of the two piles. So if the cards were labeled 0, 1, 2, …, 51, the new sequence is 0, 26, 1, 27, 2, 28, … With repeated in-shuffles, shall we ever get back the original order
How to shuffle like a pro
And try to Ripple the cards. You're going to Ripple half the cards. So your fingers go on that opposite end of the deck.
Is it possible to shuffle cards into order : If you truly randomise the deck, the chances of the cards ending up in perfect order – spades, then hearts, diamonds and clubs – are around 1 in 10 to the power 68 (or 1 followed by 68 zeros). That's a huge number, roughly equal to the number of atoms in our galaxy. Yet card players report it happening.
In 1992, Bayer and Diaconis showed that after seven random riffle shuffles of a deck of 52 cards, every configuration is nearly equally likely. 52! is approximately 8.0658e67. For an exact representation, view a factorial table or try a "new-school" calculator, one that understands long integers. A billion years currently equals 3.155692608e16 seconds; however, the addition of leap seconds due to the deceleration of Earth's orbit introduces some variation.
What is a proper shuffle
The first type of Shuffle is a riffle Shuffle this is one of the most commonly used shuffles you cut the deck roughly in half then you drop cards. One at a time from each pile.The result in that cell is 8, which is the number of perfect shuffles required to restore a 52-card deck to its original order.Shuffling is an energizing and fast-paced dance move that stems from the 1980s Australian rave scene. It continues to be popular at clubs, festivals, and anywhere that has a dance floor, and while it might look a little complicated to perform, it's actually super simple once you get started! If you truly randomise the deck, the chances of the cards ending up in perfect order – spades, then hearts, diamonds and clubs – are around 1 in 10 to the power 68 (or 1 followed by 68 zeros). That's a huge number, roughly equal to the number of atoms in our galaxy. Yet card players report it happening.
What is a perfectly shuffled deck of cards : A perfect shuffle is performed by splitting the deck into a top part and a bottom part and then (starting with the bottom part) repeatedly taking the bottom card from each part and placing them on top of a new deck. The process called an in-shuffle is shown for a deck of 8 cards below.
How big is 100000 factorial : Factorial
1000
4.023872601×102567
3249
6.412337688×1010000
10000
2.846259681×1035659
25206
1.205703438×10100000
100000
2.824229408×10456573
Why is 52 factorial so special
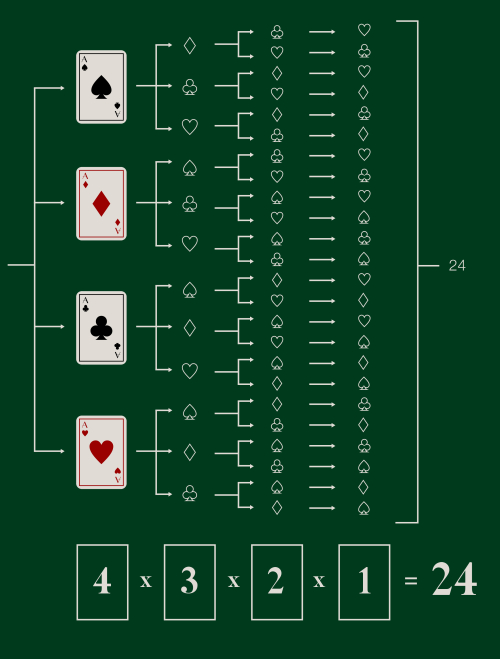
The number of possible ways to order a pack of 52 cards is '52! ' (“52 factorial”) which means multiplying 52 by 51 by 50… all the way down to 1. The number you get at the end is 8×10^67 (8 with 67 '0's after it), essentially meaning that a randomly shuffled deck has never been seen before and will never be seen again. And slide your left foot. Back. Okay now go back right foot. Up. Go back up.One trillion factorial is approximately 1.40366116 × 1011,565,705,518,103.
Why is 0 factorial is 1 : This still counts as a way of arranging it, so by definition, a zero factorial is equal to one, just as 1! is equal to one because there is only a single possible arrangement of this data set.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort What is the order of the perfect shuffle? Weitere Antworten – How to properly shuffle cards
And then you're going to peel up a block of cards pivoting. It like you're a big block your index finger yeah yeah big block and that'll give you more cards to shuffle. With.Riffle seven times and you'll have a sufficiently random ordering of cards, an ordering that has likely never existed before. In other words, it's unlikely you'll ever shuffle two decks the same. The card shuffling result appears in a Numberphile video from 2015, along with a number of other card shuffling facts.We know from the Fun Fact Seven Shuffles that 7 random riffle shuffles are enough to make almost every configuration equally likely in a deck of 52 cards.
What is a perfect in shuffle of a deck of 52 cards : A perfect in-shuffle of a deck of 52 cards is defined as follows. The deck is cut in half followed by interleaving of the two piles. So if the cards were labeled 0, 1, 2, …, 51, the new sequence is 0, 26, 1, 27, 2, 28, … With repeated in-shuffles, shall we ever get back the original order
How to shuffle like a pro
And try to Ripple the cards. You're going to Ripple half the cards. So your fingers go on that opposite end of the deck.
Is it possible to shuffle cards into order : If you truly randomise the deck, the chances of the cards ending up in perfect order – spades, then hearts, diamonds and clubs – are around 1 in 10 to the power 68 (or 1 followed by 68 zeros). That's a huge number, roughly equal to the number of atoms in our galaxy. Yet card players report it happening.
In 1992, Bayer and Diaconis showed that after seven random riffle shuffles of a deck of 52 cards, every configuration is nearly equally likely.
52! is approximately 8.0658e67. For an exact representation, view a factorial table or try a "new-school" calculator, one that understands long integers. A billion years currently equals 3.155692608e16 seconds; however, the addition of leap seconds due to the deceleration of Earth's orbit introduces some variation.
What is a proper shuffle
The first type of Shuffle is a riffle Shuffle this is one of the most commonly used shuffles you cut the deck roughly in half then you drop cards. One at a time from each pile.The result in that cell is 8, which is the number of perfect shuffles required to restore a 52-card deck to its original order.Shuffling is an energizing and fast-paced dance move that stems from the 1980s Australian rave scene. It continues to be popular at clubs, festivals, and anywhere that has a dance floor, and while it might look a little complicated to perform, it's actually super simple once you get started!
If you truly randomise the deck, the chances of the cards ending up in perfect order – spades, then hearts, diamonds and clubs – are around 1 in 10 to the power 68 (or 1 followed by 68 zeros). That's a huge number, roughly equal to the number of atoms in our galaxy. Yet card players report it happening.
What is a perfectly shuffled deck of cards : A perfect shuffle is performed by splitting the deck into a top part and a bottom part and then (starting with the bottom part) repeatedly taking the bottom card from each part and placing them on top of a new deck. The process called an in-shuffle is shown for a deck of 8 cards below.
How big is 100000 factorial : Factorial
Why is 52 factorial so special
The number of possible ways to order a pack of 52 cards is '52! ' (“52 factorial”) which means multiplying 52 by 51 by 50… all the way down to 1. The number you get at the end is 8×10^67 (8 with 67 '0's after it), essentially meaning that a randomly shuffled deck has never been seen before and will never be seen again.
And slide your left foot. Back. Okay now go back right foot. Up. Go back up.One trillion factorial is approximately 1.40366116 × 1011,565,705,518,103.
Why is 0 factorial is 1 : This still counts as a way of arranging it, so by definition, a zero factorial is equal to one, just as 1! is equal to one because there is only a single possible arrangement of this data set.