The rank of the matrix is the dimension of the vector space obtained by its columns. The rank of a matrix cannot exceed more than the number of its rows or columns. The rank of the null matrix is zero.3
For example, if we consider the identity matrix of order 3 × 3, all its rows (or columns) are linearly independent and hence its rank is 3.A 2 × 2 matrix 𝐴 , where 𝐴 ≠ 0 × , has rank R K ( 𝐴 ) = 1 if and only if it has a determinant d e t ( 𝐴 ) = 0 . We can prove this corollary as follows. The only 2 × 2 submatrix of 𝐴 is itself. If d e t ( 𝐴 ) = 0 , then the largest possible square submatrix with a nonzero determinant is a 1 × 1 matrix.
What is rank 1 of a matrix : Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product.
Why is matrix rank 1
The column space of A is R1. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1. 1 4 5 A = 2 8 10 2 Page 3 has rank 1 because each of its columns is a multiple of the first column.
Can a matrix be rank 0 : The zero matrix is the only matrix whose rank is 0.
The matrix of size (3×4) can have the rank = min(3,4). The maximum possible rank of the matrix is the minimum value of the number of rows and number of columns of the matrix . So here the maximum possible rank of the matrix will be 3. The rank is the number of pivot positions in a row-reduced form of the original matrix and indicates the number of columns (or rows) that are linearly independent, i.e. the dimension of the column space. Since row rank = column rank, the rank of a 3×5 3 × 5 matrix cannot be greater than 3.
What is the rank of matrix A =[ 1 2 3 4
2
The correct Answer is:2.Sure, you can have a matrix of rank 4, or 5 or 6 or any higher integer. It's just you need longer vectors, spaces of higher dimension than 3 (indeed the Cliff's notes explicitly state 3-vectors).The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 . For most items, a sales rank of zero simply means that the item has never sold, or has not sold in a long, long, long time. This will apply to most of the items that have no sales rank, but there are sometimes exceptions. Some categories don't offer up sales ranks for all items. Electronics is an example.
What is the rank of a 5×7 matrix : The rank of a matrix A equals the number of pivot positions which the matrix has. If A is either a 7×5 matrix or a 5 x 7 matrix, the largest number of pivot positions that A could have is 5. Thus the largest possible value for rank A is 5.
What is the rank of 1/4, 5 2 6 8 3 7 22 : Answer: The rank of the given matrix is 3.
What is the rank of 1 2 3 1 4 2 2 6 5
Expert-Verified Answer. The rank of the given matrix is 2. The zero matrix is the only matrix whose rank is 0.The zero matrix is the only matrix whose rank is 0.
Can a matrix have rank 1 : Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort What is a rank in a matrix? Weitere Antworten – What is the rank of a matrix
The rank of a Matrix Definition
The rank of the matrix is the dimension of the vector space obtained by its columns. The rank of a matrix cannot exceed more than the number of its rows or columns. The rank of the null matrix is zero.3
For example, if we consider the identity matrix of order 3 × 3, all its rows (or columns) are linearly independent and hence its rank is 3.A 2 × 2 matrix 𝐴 , where 𝐴 ≠ 0 × , has rank R K ( 𝐴 ) = 1 if and only if it has a determinant d e t ( 𝐴 ) = 0 . We can prove this corollary as follows. The only 2 × 2 submatrix of 𝐴 is itself. If d e t ( 𝐴 ) = 0 , then the largest possible square submatrix with a nonzero determinant is a 1 × 1 matrix.
What is rank 1 of a matrix : Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product.
Why is matrix rank 1
The column space of A is R1. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1. 1 4 5 A = 2 8 10 2 Page 3 has rank 1 because each of its columns is a multiple of the first column.
Can a matrix be rank 0 : The zero matrix is the only matrix whose rank is 0.
The matrix of size (3×4) can have the rank = min(3,4). The maximum possible rank of the matrix is the minimum value of the number of rows and number of columns of the matrix . So here the maximum possible rank of the matrix will be 3.
The rank is the number of pivot positions in a row-reduced form of the original matrix and indicates the number of columns (or rows) that are linearly independent, i.e. the dimension of the column space. Since row rank = column rank, the rank of a 3×5 3 × 5 matrix cannot be greater than 3.
What is the rank of matrix A =[ 1 2 3 4
2
The correct Answer is:2.Sure, you can have a matrix of rank 4, or 5 or 6 or any higher integer. It's just you need longer vectors, spaces of higher dimension than 3 (indeed the Cliff's notes explicitly state 3-vectors).The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 .
For most items, a sales rank of zero simply means that the item has never sold, or has not sold in a long, long, long time. This will apply to most of the items that have no sales rank, but there are sometimes exceptions. Some categories don't offer up sales ranks for all items. Electronics is an example.
What is the rank of a 5×7 matrix : The rank of a matrix A equals the number of pivot positions which the matrix has. If A is either a 7×5 matrix or a 5 x 7 matrix, the largest number of pivot positions that A could have is 5. Thus the largest possible value for rank A is 5.
What is the rank of 1/4, 5 2 6 8 3 7 22 : Answer: The rank of the given matrix is 3.
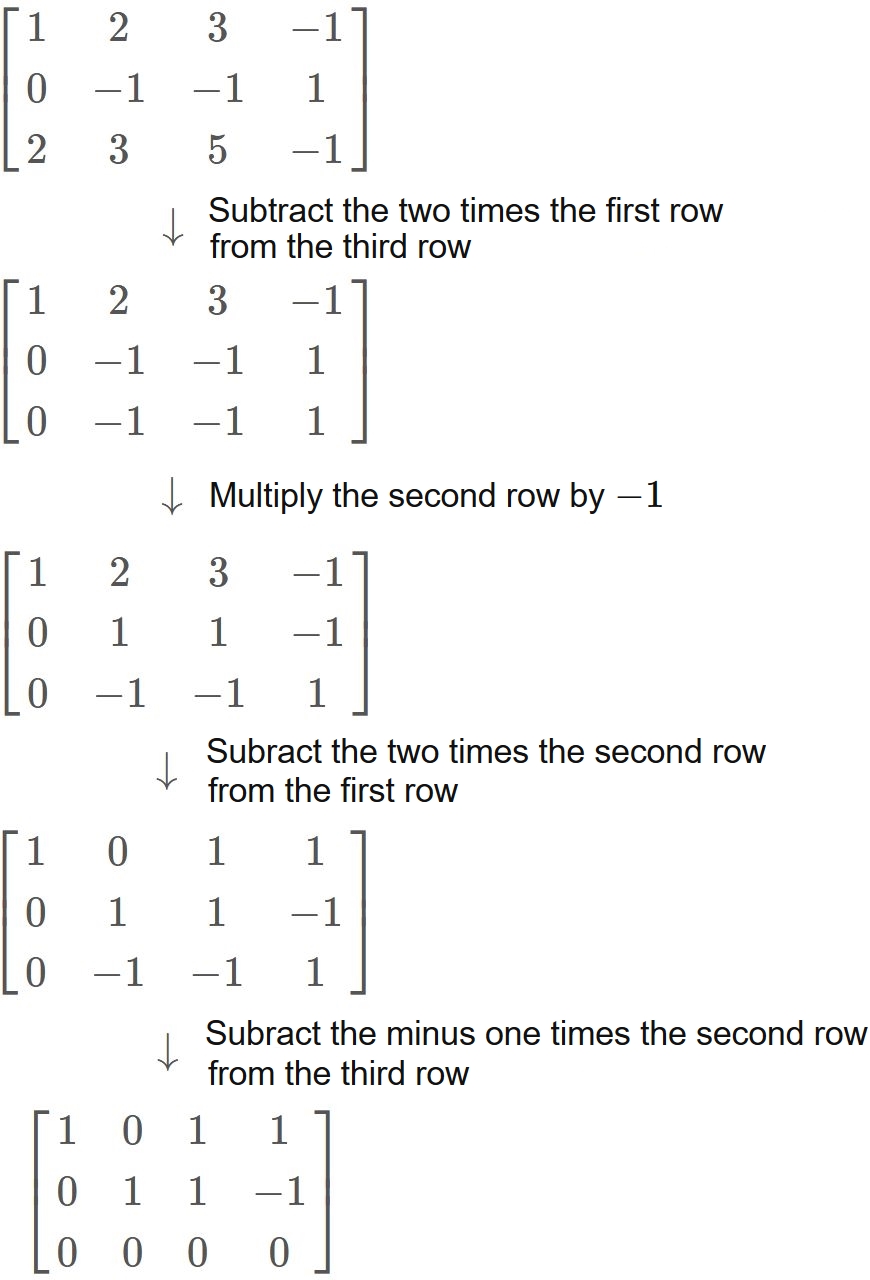
What is the rank of 1 2 3 1 4 2 2 6 5
Expert-Verified Answer. The rank of the given matrix is 2.
The zero matrix is the only matrix whose rank is 0.The zero matrix is the only matrix whose rank is 0.
Can a matrix have rank 1 : Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.