The rank of an augmented matrix can be found by performing elementary row operations on an augmented matrix and counting the number of rows without zeros. Comparing the rank of an augmented matrix to the rank of the coefficient matrix can be used to determine if there is a solution to the system of linear equations.The matrix of the determinant is non-singular and not invertible. The matrix of the determinant may be a zero matrix. The system of equations associated with the matrix is linearly dependent.Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix: Swap the positions of two of the rows. Multiply one of the rows by a nonzero scalar.
What is the coefficient of a matrix : In mathematics, a matrix coefficient (or matrix element) is a function on a group of a special form, which depends on a linear representation of the group and additional data.
What is rank 1 matrix
A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product. Theorem: outer product representation of a rank-one matrix. Every rank-one matrix can be written as an ''outer product'', or dyad.
Why is matrix rank 1 : The column space of A is R1. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1. 1 4 5 A = 2 8 10 2 Page 3 has rank 1 because each of its columns is a multiple of the first column.
which is called the determinant for this system of equation. Determinants are defined only for square matrices. If the determinant of a matrix is 0, the matrix is said to be singular, and if the determinant is 1, the matrix is said to be unimodular. The maximum rank of a 2×3 matrix is only 2.
Which is better Gauss elimination or Gauss-Jordan method
Therefore Gauss Elimination Method is more efficient than the Gauss Jordan Elimination method. Gaussian Elimination helps to put a matrix in row echelon form, while Gauss-Jordan Elimination puts a matrix in reduced row echelon form.The Gauss-Jordan Method is similar to Gaussian Elimination, except that the entries both above and below each pivot are targeted (zeroed out). After performing Gaussian Elimination on a matrix, the result is in row echelon form. After the Gauss-Jordan Method, the result is in reduced row echelon form.The rank of the matrix refers to the number of linearly independent rows or columns in the matrix. ρ(A) is used to denote the rank of matrix A. A matrix is said to be of rank zero when all of its elements become zero. The rank of the matrix is the dimension of the vector space obtained by its columns. Example 2: Multiple Linear Regression
In the regression below, X 1 X_1 X1 and X 2 X_2 X2, are both independent variables, so the values 1.5 and -0.8 are both regression coefficients.
How to identify rank 1 matrix : If neither u nor v is zero, then uvT is nonzero, so its rank is at least 1. If either u or v is zero, then the product uvT is the zero matrix, which has rank zero. Note that also the converse holds: if an m×n matrix A has rank 1, then A=uvT for suitable column vectors u and v.
What is a rank 1 matrix : Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
What is the determinant of a rank 1 matrix
What is the determinant of a rank-one matrix – Quora. This question is rather strange, but the answer is very simple : if A is a square matrix of order n and Rank A = r , 1 < r < n then | A | = 0 ; if r = n then | A | ≠ 0 . Matrices with determinant 1 preserve volume. If all points inside a shape are transformed by the matrix to form a new shape, the proportional change in area (or volume) is the determinant of the matrix. For example if the determinant of a matrix A is 5, then a unit cube will transform into a shape with volume 5×1=5.Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product.
Can a 2×2 matrix have rank 1 : Since a zero determinant of any n x n matrix implies that the rank must be less than n, the rank for a 2×2 matrix must be 0 (null matrix) or 1. As a standard exercise in linear algebra, we can show that any rank-1 matrix may be written as the outer product of two vectors, a well-documented result in textbooks.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort What are 3×3 matrices of rank 1? Weitere Antworten – What is the rank of an augmented matrix
The rank of an augmented matrix can be found by performing elementary row operations on an augmented matrix and counting the number of rows without zeros. Comparing the rank of an augmented matrix to the rank of the coefficient matrix can be used to determine if there is a solution to the system of linear equations.The matrix of the determinant is non-singular and not invertible. The matrix of the determinant may be a zero matrix. The system of equations associated with the matrix is linearly dependent.Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix: Swap the positions of two of the rows. Multiply one of the rows by a nonzero scalar.
What is the coefficient of a matrix : In mathematics, a matrix coefficient (or matrix element) is a function on a group of a special form, which depends on a linear representation of the group and additional data.
What is rank 1 matrix
A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product. Theorem: outer product representation of a rank-one matrix. Every rank-one matrix can be written as an ''outer product'', or dyad.
Why is matrix rank 1 : The column space of A is R1. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1. 1 4 5 A = 2 8 10 2 Page 3 has rank 1 because each of its columns is a multiple of the first column.
which is called the determinant for this system of equation. Determinants are defined only for square matrices. If the determinant of a matrix is 0, the matrix is said to be singular, and if the determinant is 1, the matrix is said to be unimodular.
The maximum rank of a 2×3 matrix is only 2.
Which is better Gauss elimination or Gauss-Jordan method
Therefore Gauss Elimination Method is more efficient than the Gauss Jordan Elimination method. Gaussian Elimination helps to put a matrix in row echelon form, while Gauss-Jordan Elimination puts a matrix in reduced row echelon form.The Gauss-Jordan Method is similar to Gaussian Elimination, except that the entries both above and below each pivot are targeted (zeroed out). After performing Gaussian Elimination on a matrix, the result is in row echelon form. After the Gauss-Jordan Method, the result is in reduced row echelon form.The rank of the matrix refers to the number of linearly independent rows or columns in the matrix. ρ(A) is used to denote the rank of matrix A. A matrix is said to be of rank zero when all of its elements become zero. The rank of the matrix is the dimension of the vector space obtained by its columns.
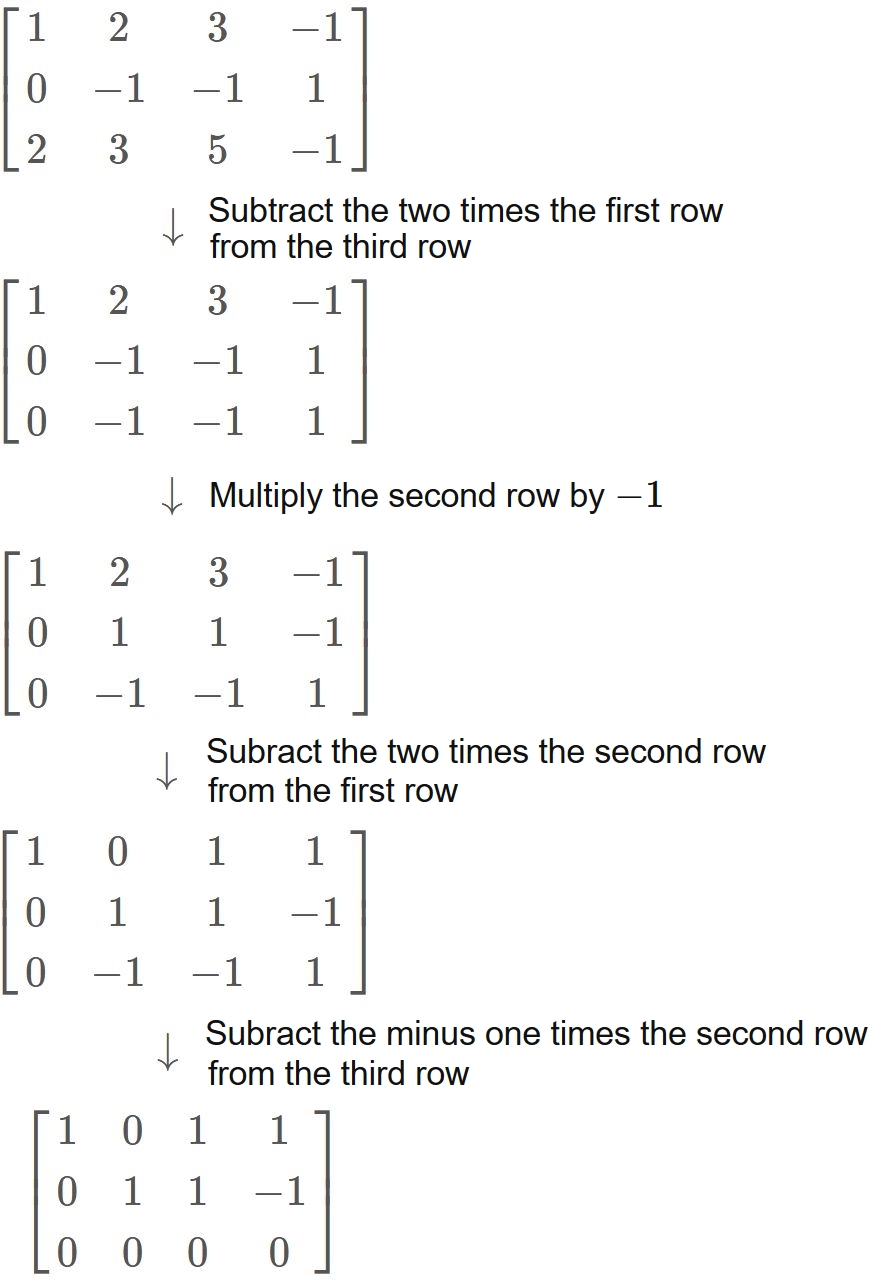
Example 2: Multiple Linear Regression
In the regression below, X 1 X_1 X1 and X 2 X_2 X2, are both independent variables, so the values 1.5 and -0.8 are both regression coefficients.
How to identify rank 1 matrix : If neither u nor v is zero, then uvT is nonzero, so its rank is at least 1. If either u or v is zero, then the product uvT is the zero matrix, which has rank zero. Note that also the converse holds: if an m×n matrix A has rank 1, then A=uvT for suitable column vectors u and v.
What is a rank 1 matrix : Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
What is the determinant of a rank 1 matrix
What is the determinant of a rank-one matrix – Quora. This question is rather strange, but the answer is very simple : if A is a square matrix of order n and Rank A = r , 1 < r < n then | A | = 0 ; if r = n then | A | ≠ 0 .
Matrices with determinant 1 preserve volume. If all points inside a shape are transformed by the matrix to form a new shape, the proportional change in area (or volume) is the determinant of the matrix. For example if the determinant of a matrix A is 5, then a unit cube will transform into a shape with volume 5×1=5.Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product.
Can a 2×2 matrix have rank 1 : Since a zero determinant of any n x n matrix implies that the rank must be less than n, the rank for a 2×2 matrix must be 0 (null matrix) or 1. As a standard exercise in linear algebra, we can show that any rank-1 matrix may be written as the outer product of two vectors, a well-documented result in textbooks.