V každém pravoúhlém trojúhelníku platí , kde je délka přepony, , jsou délky jeho odvěsen. Jiná formulace věty. Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců nad jeho odvěsnami.umime.to/FV2
Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.
Co je to Obracena Pythagorova věta : Jestliže se v trojúhelníku obsah čtvercem nad jeho nejdelší stranou rovná součtu obsahů čtverců nad jeho kratšími stranami, pak je tento trojúhelník pravoúhlý.
Kde se používá Pythagorova věta
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Co rekl Pythagoras : Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlých trojúhelníků v rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran. Pythagorovi se připisuje zavedení pojmu filosofie (filein = milovat, sofos = moudrý), stejně tak i pojem kosmos (kosmeó = zdobit), a dokonce i pojem matematika. Přestože se Pythagoras proslavil především svou naukou o zákonitostech pravoúhlého trojúhelníku, považoval za primární a nejdokonalejší tvar kruh a kouli.
Co vymyslel Pythagoras
Ta je snad nejslavnější matematickou větou vůbec. Objevil ji v 6. století před naším letopočtem řecký filosof a matematik Pythagoras. „Obsah čtverce sestrojeného nad přeponou (nejdelší stranou) pravoúhlého rovinného trojúhelníku je roven součtu obsahů čtverců nad jeho odvěsnami (dvěma kratšími stranami),“ pamatujetePythagoras- zakladatel, matematik, astronom, který se narodil na ostrově Samos. Pralátkou a podstatou všeho je číslo (1–10, nejdokonalejší je magická 10). Vše je kombinací čísel. Známá je i Pythagorova věta.Součet obsahů čtverců nad odvěsnami pravoúhlého trojúhelníku je roven obsahu čtverce nad přeponou. Praktická znalost této věty sahá ovšem do dávné minulosti: využívali ji staří Číňané, Indové i Babyloňané. Pythagorovi a jeho žákům se připisuje důkaz věty.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Na co se používá Pythagorova věta? Weitere Antworten – Kdy platí Pythagorova věta
V každém pravoúhlém trojúhelníku platí , kde je délka přepony, , jsou délky jeho odvěsen. Jiná formulace věty. Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců nad jeho odvěsnami.umime.to/FV2
Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.
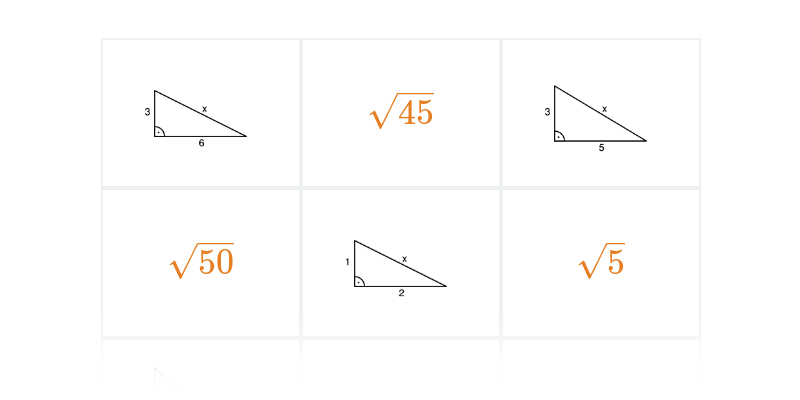
Co je to Obracena Pythagorova věta : Jestliže se v trojúhelníku obsah čtvercem nad jeho nejdelší stranou rovná součtu obsahů čtverců nad jeho kratšími stranami, pak je tento trojúhelník pravoúhlý.
Kde se používá Pythagorova věta
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Co rekl Pythagoras : Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlých trojúhelníků v rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran.
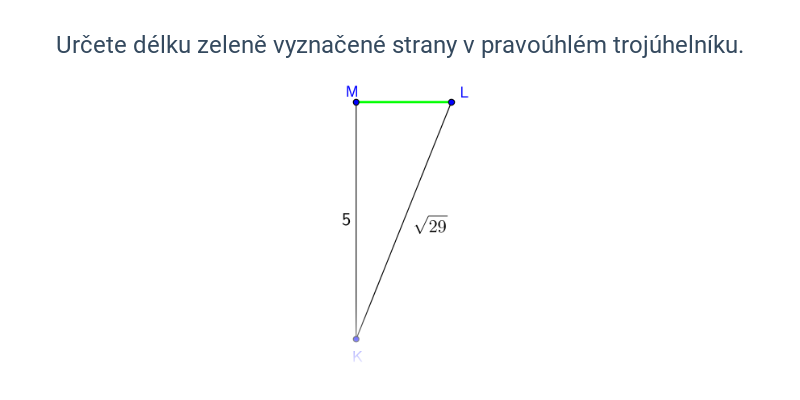
Pythagorovi se připisuje zavedení pojmu filosofie (filein = milovat, sofos = moudrý), stejně tak i pojem kosmos (kosmeó = zdobit), a dokonce i pojem matematika. Přestože se Pythagoras proslavil především svou naukou o zákonitostech pravoúhlého trojúhelníku, považoval za primární a nejdokonalejší tvar kruh a kouli.
Co vymyslel Pythagoras
Ta je snad nejslavnější matematickou větou vůbec. Objevil ji v 6. století před naším letopočtem řecký filosof a matematik Pythagoras. „Obsah čtverce sestrojeného nad přeponou (nejdelší stranou) pravoúhlého rovinného trojúhelníku je roven součtu obsahů čtverců nad jeho odvěsnami (dvěma kratšími stranami),“ pamatujetePythagoras- zakladatel, matematik, astronom, který se narodil na ostrově Samos. Pralátkou a podstatou všeho je číslo (1–10, nejdokonalejší je magická 10). Vše je kombinací čísel. Známá je i Pythagorova věta.Součet obsahů čtverců nad odvěsnami pravoúhlého trojúhelníku je roven obsahu čtverce nad přeponou. Praktická znalost této věty sahá ovšem do dávné minulosti: využívali ji staří Číňané, Indové i Babyloňané. Pythagorovi a jeho žákům se připisuje důkaz věty.