Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Krychle
Počet vrcholů
8
Počet hran
12
Počet stěn
6
Úhel u vrcholu
90°
Krychle je geometrické těleso, které má tři rozměry. Skládá se ze šesti navzájem shodných čtverců. Kvádr je geometrické těleso, které má tři rozměry. Skládá se ze šesti obdélníků, přičemž každé dva obdélníky, které jsou proti sobě jsou shodné.
Kolik je šití kvádru : Síť kvádru se skládá ze všech jeho šesti stěn (obr. 3.8.2). V =abc. S =2ab+2(ac+bc)=2(ab+ac+bc).
Kolik má kvádr stran
Kvádr má šest stěn obdélníkového tvaru (nebo 2 čtvercové + 4 obdélníkové) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran, z nichž čtveřice rovnoběžných má vždy shodnou délku. Každé dvě stěny kvádru jsou rovnoběžné nebo kolmé.
Jak se vypočítá obsah kvádru : Pro výpočet obsahu kvádru stačí znát délky tří jeho stran. Do kalkulačky tedy zadejte šířku kvádru a, délku kvádru b a výšku kvádru c. Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Pravidelný dvanáctistěn
Stěny pravidelného dvanáctistěnu jsou tvořeny dvanácti shodnými pravidelnými pětiúhelníky. Toto těleso má dvacet vrcholů a třicet hran, viz obr. Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Kolik krychli se vejde do kvádru
(8) Jedna stěna krychle má obsah 25 cm2. (9) Můžeme udělat celkem 4 patra, každé s 35 krychlemi. Do kvádru se vejde celkem 140 krychlí.Stěny: Kvádr má celkem šest stěn, které jsou ve dvojicích protilehlé, rovnoběžné a stejně velké. Tyto stěny jsou obdélníky. Hrany: Kvádr má dvanáct hran, které spojují vrcholy stěn.Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle. Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Kolik hran má Osmistěn : umime.to/FV6
mnohostěn
počet stěn
počet hran
čtyřstěn
4
6
krychle
6
12
osmistěn
8
12
dvanáctistěn
12
30
Kolik hran má Ctyrsten : Stěny pravidelného čtyřstěnu jsou tvořeny čtyřmi shodnými rovnostrannými trojúhelníky. Toto těleso má čtyři vrcholy a šest hran, viz obr.
Jaký je vzoreček pro povrch kvádru
Kvádr má šest stěn a všechny jsou tvořené obdélníky, vždy dvě jsou stejně velké. Povrch kvádru vypočítáme jako: S = 2(ab + bc + ac). Výška v kvádru je rovna trojnásobku délky kratšího rozměru podstavy.Kvádr má šest stěn obdélníkového tvaru (nebo 2 čtvercové + 4 obdélníkové) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran, z nichž čtveřice rovnoběžných má vždy shodnou délku. Každé dvě stěny kvádru jsou rovnoběžné nebo kolmé.
Jak se pocita plášť kvádru : Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = a b c V = abc V=abc. Objem krychle vypočítáme stejným způsobem.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Kolik bočních stěn má kvádr? Weitere Antworten – Kolik má kvádr stěn
Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Krychle je geometrické těleso, které má tři rozměry. Skládá se ze šesti navzájem shodných čtverců. Kvádr je geometrické těleso, které má tři rozměry. Skládá se ze šesti obdélníků, přičemž každé dva obdélníky, které jsou proti sobě jsou shodné.
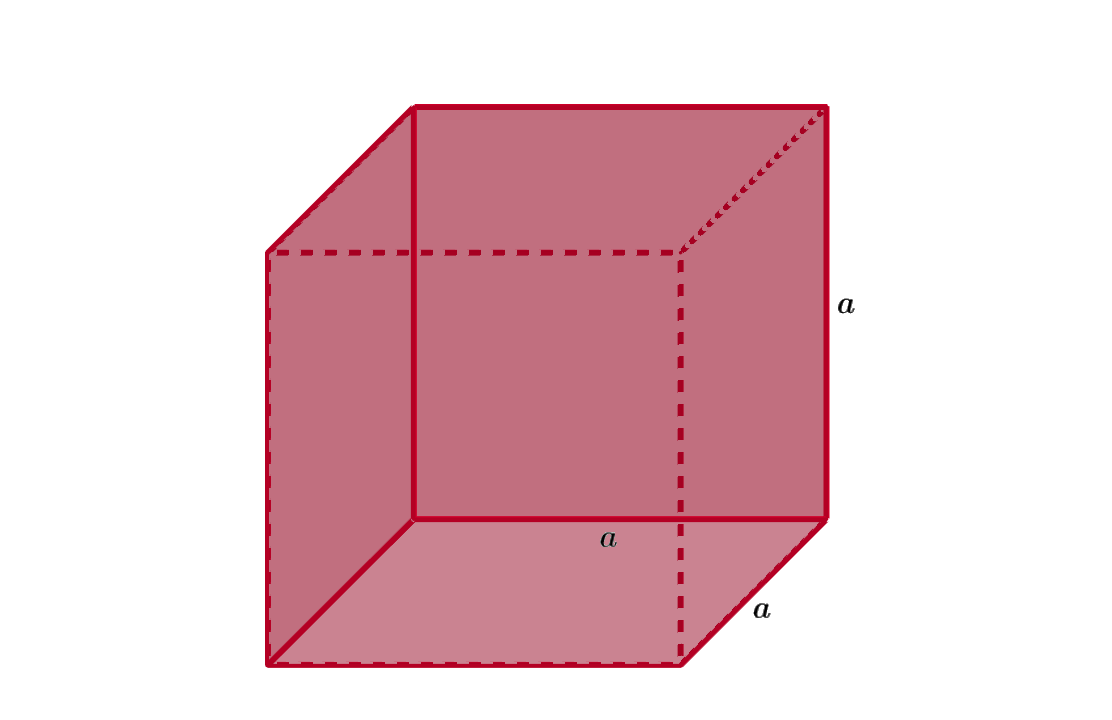
Kolik je šití kvádru : Síť kvádru se skládá ze všech jeho šesti stěn (obr. 3.8.2). V =abc. S =2ab+2(ac+bc)=2(ab+ac+bc).
Kolik má kvádr stran
Kvádr má šest stěn obdélníkového tvaru (nebo 2 čtvercové + 4 obdélníkové) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran, z nichž čtveřice rovnoběžných má vždy shodnou délku. Každé dvě stěny kvádru jsou rovnoběžné nebo kolmé.
Jak se vypočítá obsah kvádru : Pro výpočet obsahu kvádru stačí znát délky tří jeho stran. Do kalkulačky tedy zadejte šířku kvádru a, délku kvádru b a výšku kvádru c. Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Pravidelný dvanáctistěn
Stěny pravidelného dvanáctistěnu jsou tvořeny dvanácti shodnými pravidelnými pětiúhelníky. Toto těleso má dvacet vrcholů a třicet hran, viz obr.
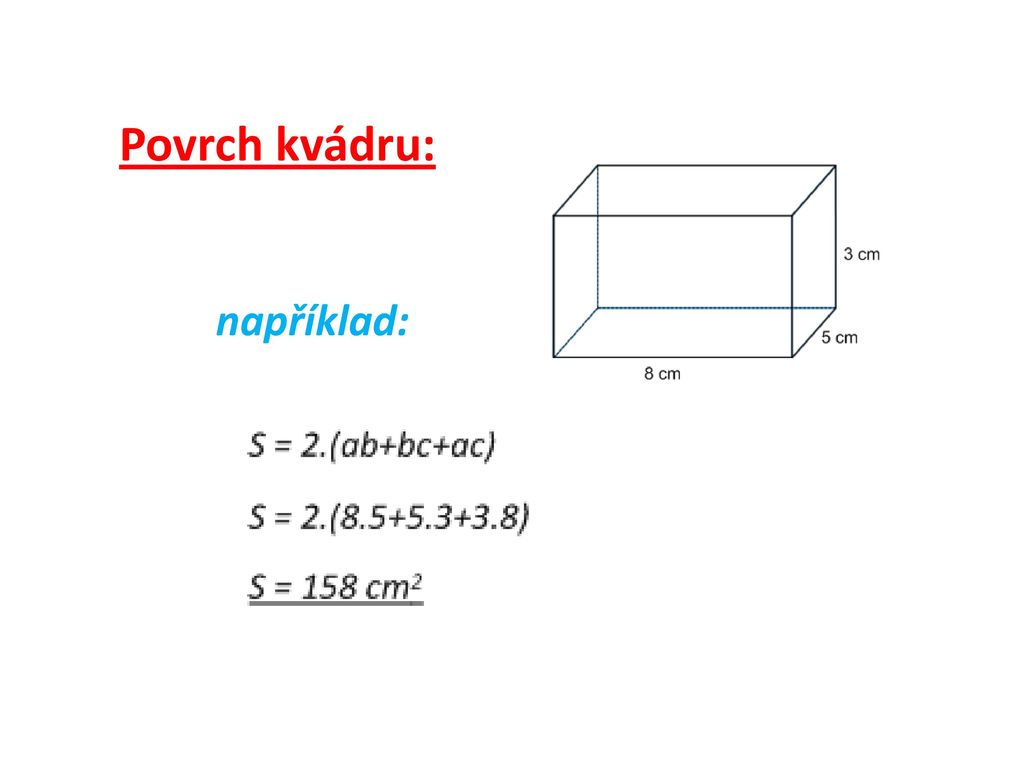
Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Kolik krychli se vejde do kvádru
(8) Jedna stěna krychle má obsah 25 cm2. (9) Můžeme udělat celkem 4 patra, každé s 35 krychlemi. Do kvádru se vejde celkem 140 krychlí.Stěny: Kvádr má celkem šest stěn, které jsou ve dvojicích protilehlé, rovnoběžné a stejně velké. Tyto stěny jsou obdélníky. Hrany: Kvádr má dvanáct hran, které spojují vrcholy stěn.Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle.
Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Kolik hran má Osmistěn : umime.to/FV6
Kolik hran má Ctyrsten : Stěny pravidelného čtyřstěnu jsou tvořeny čtyřmi shodnými rovnostrannými trojúhelníky. Toto těleso má čtyři vrcholy a šest hran, viz obr.
Jaký je vzoreček pro povrch kvádru
Kvádr má šest stěn a všechny jsou tvořené obdélníky, vždy dvě jsou stejně velké. Povrch kvádru vypočítáme jako: S = 2(ab + bc + ac).
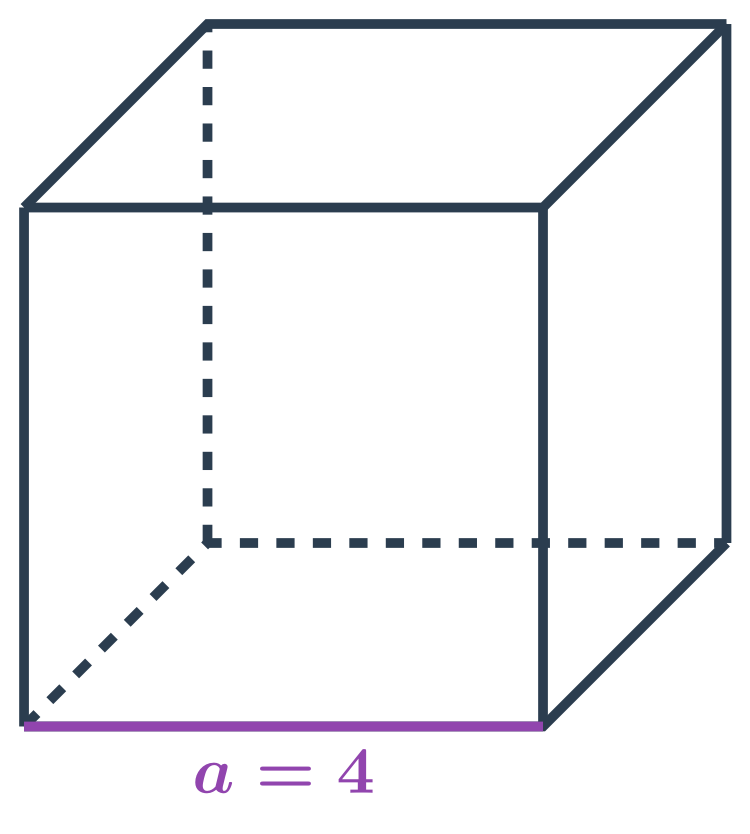
Výška v kvádru je rovna trojnásobku délky kratšího rozměru podstavy.Kvádr má šest stěn obdélníkového tvaru (nebo 2 čtvercové + 4 obdélníkové) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran, z nichž čtveřice rovnoběžných má vždy shodnou délku. Každé dvě stěny kvádru jsou rovnoběžné nebo kolmé.
Jak se pocita plášť kvádru : Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = a b c V = abc V=abc. Objem krychle vypočítáme stejným způsobem.