Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.Definice: Zobrazení v rovině se nazývá podobným zobrazením (podobností), jestliže každé úsečce AB přiřazuje úsečku A´B´ pro jejíž velikost platí . Koeficient k nazýváme poměr podobnosti.
Jak zapsat podobnost trojúhelníku : Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm.
Kdy nelze sestrojit trojúhelník
Dneska si ukážeme, jak poznat ze zadání délek stran trojúhelníku, že trojúhelník nejde narýsovat. Takovému postupu říkáme TROJÚHELNÍKOVÁ NEROVNOST – V každém trojúhelníku platí, že součet délek libovolných dvou jeho stran je větší než délka strany třetí.
Jak zjistit jestli je trojúhelník pravoúhlý : Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.
Dva geometrické útvary nazýváme podobné, jestliže poměry délek všech dvojic odpovídajících si úseček těchto útvarů se rovnají témuž číslu k > 0. Toto číslo nazýváme poměr podobnosti. Každé dva odpovídající si úhly podobných útvarů jsou shodné. trojúhelníku): • Věta sss: Shodují-li se dva trojúhelníky ve všech třech stranách, jsou shodné.
Co je to podobnost
podobnost (obecný pojem) – vlastnost různých věcí nebo dějů, kdy se liší (jen) některé charakteristiky nebo vlastnosti těchto věcí či se jejich charakteristiky liší jen málo.Přímá a nepřímá shodnost
Shodnost zachovávající orientaci se nazývá přímá neboli přemístění. Shodnost měnící orientaci se nazývá nepřímá. Posunutí a otočení (a tedy i středová souměrnost) jsou přímé shodnosti (přemístění), zachovávají orientaci. (Posunuté) osové souměrnosti jsou nepřímé shodnosti, mění orientaci.Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý. Věta usu Trojúhelník lze sestrojit podle věty usu, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. Věta Ssu Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich. Velikost zadaného úhlu je menší než 180°.
Jaký trojúhelník nelze sestrojit : Dneska si ukážeme, jak poznat ze zadání délek stran trojúhelníku, že trojúhelník nejde narýsovat. Takovému postupu říkáme TROJÚHELNÍKOVÁ NEROVNOST – V každém trojúhelníku platí, že součet délek libovolných dvou jeho stran je větší než délka strany třetí.
Jak zjistit Preponu : Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna.
Jak Vypočítám Přeponu pravoúhlého trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 . Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).
Jak se počítá věta SSS : Věta SSS: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. 1. Narýsuj ∆ABC, je-li dáno: AB = c =7,6 cm, BC = a = 4,2 cm, AC = b = 5,6 cm.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Kdy jsou si trojúhelníky podobne? Weitere Antworten – Kdy jsou trojúhelníky shodné
Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.Definice: Zobrazení v rovině se nazývá podobným zobrazením (podobností), jestliže každé úsečce AB přiřazuje úsečku A´B´ pro jejíž velikost platí . Koeficient k nazýváme poměr podobnosti.
Jak zapsat podobnost trojúhelníku : Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm.
Kdy nelze sestrojit trojúhelník
Dneska si ukážeme, jak poznat ze zadání délek stran trojúhelníku, že trojúhelník nejde narýsovat. Takovému postupu říkáme TROJÚHELNÍKOVÁ NEROVNOST – V každém trojúhelníku platí, že součet délek libovolných dvou jeho stran je větší než délka strany třetí.
Jak zjistit jestli je trojúhelník pravoúhlý : Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.
Dva geometrické útvary nazýváme podobné, jestliže poměry délek všech dvojic odpovídajících si úseček těchto útvarů se rovnají témuž číslu k > 0. Toto číslo nazýváme poměr podobnosti. Každé dva odpovídající si úhly podobných útvarů jsou shodné.
trojúhelníku): • Věta sss: Shodují-li se dva trojúhelníky ve všech třech stranách, jsou shodné.
Co je to podobnost
podobnost (obecný pojem) – vlastnost různých věcí nebo dějů, kdy se liší (jen) některé charakteristiky nebo vlastnosti těchto věcí či se jejich charakteristiky liší jen málo.Přímá a nepřímá shodnost
Shodnost zachovávající orientaci se nazývá přímá neboli přemístění. Shodnost měnící orientaci se nazývá nepřímá. Posunutí a otočení (a tedy i středová souměrnost) jsou přímé shodnosti (přemístění), zachovávají orientaci. (Posunuté) osové souměrnosti jsou nepřímé shodnosti, mění orientaci.Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.
Věta usu Trojúhelník lze sestrojit podle věty usu, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. Věta Ssu Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich. Velikost zadaného úhlu je menší než 180°.
Jaký trojúhelník nelze sestrojit : Dneska si ukážeme, jak poznat ze zadání délek stran trojúhelníku, že trojúhelník nejde narýsovat. Takovému postupu říkáme TROJÚHELNÍKOVÁ NEROVNOST – V každém trojúhelníku platí, že součet délek libovolných dvou jeho stran je větší než délka strany třetí.
Jak zjistit Preponu : Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna.
Jak Vypočítám Přeponu pravoúhlého trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
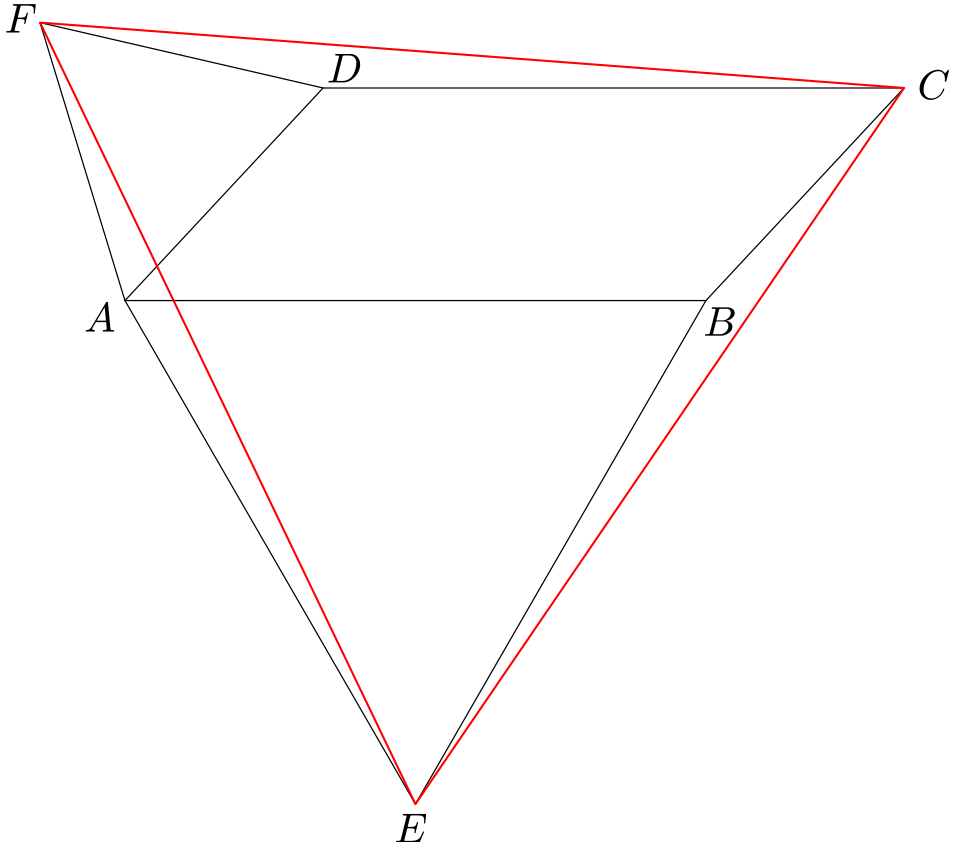
Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).
Jak se počítá věta SSS : Věta SSS: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. 1. Narýsuj ∆ABC, je-li dáno: AB = c =7,6 cm, BC = a = 4,2 cm, AC = b = 5,6 cm.