Goniometrické funkce (nebo též trigonometrické funkce) je skupina funkcí, které dávají do vztahu úhel v pravoúhlém trojúhelníku a poměr dvou jeho stran. Goniometrické funkce mají široké využití v geometrii a mnoho praktických aplikací (například v navigaci, nebeské mechanice či geodézii).Jako goniometrické funkce se v matematice nazývá skupina šesti funkcí velikosti úhlu používaných například při zkoumání trojúhelníků a periodických jevů.Druhou souřadnici bodu jednotkové kružnice na koncovém rameni orientovaného úhlu v základní poloze nazýváme sinus a jeho první souřadnici nazveme kosinus . Používáme značení , . Je tedy , , pro každé .
Jak poznat síň cos TG : Goniometrické funkce a pravoúhlý trojúhelník
Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Kolik je síň 0
Sinus a kvadranty
Stupně
Radiány
sin (x)
0°
0
0
90°
π/2
1
180°
π
0
270°
3π/2
−1
Kolik je cos 0 : Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0. Pro α z ⟨π/2,π⟩ definujeme sin(α) = sin(π − α) a cos(α) = −cos(π − α). Pro α z ⟨π,2π⟩ definujeme sin(α) = −sin(α − π) a cos(α) = −cos(2π − α).
Goniometrické funkce (nebo též trigonometrické funkce) je skupina funkcí, které dávají do vztahu úhel v pravoúhlém trojúhelníku a poměr dvou jeho stran. Goniometrické funkce mají široké využití v geometrii a mnoho praktických aplikací (například v navigaci, nebeské mechanice či geodézii). Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.
Kolik je síň 120
Hodnoty sinus na jednotkové kružnici
x (úhel)
45°
π/4
1/8
135°
3π/4
3/8
60°
π/3
1/6
120°
2π/3
1/3
Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.sin(90) = sin(2.035rad) = 0.8939. Goniometrické funkce, jako jsou sinus, kosinus, tangens a cotangens, jsou základními nástroji pro popis vztahů mezi úhly a délkami stran v pravoúhlém trojúhelníku. Tyto funkce se používají k výpočtu poměrů mezi délkami stran trojúhelníka a příslušnými úhly.
Kolik je síň 180 : Sinus a kvadranty
Stupně
Radiány
sin (x)
0°
0
0
90°
π/2
1
180°
π
0
270°
3π/2
−1
Co to je síň : Sinus je goniometrická funkce nějakého úhlu. Zapisuje se jako sin θ, kde θ je velikost úhlu. Pro ostré úhly je definována v pravoúhlém trojúhelníku jako poměr protilehlé odvěsny a přepony (nejdelší strany). Definici lze konzistentně rozšířit jak na všechna reálná čísla, tak i do oboru komplexních čísel.
Jak použít goniometrické funkce
Všechny goniometrické funkce nám ukazují vztah mezi nějakým úhlem v trojúhelníku a poměrem délek dvou stran. Zpravidla se pak nejedná o pravý úhel, ale o ty zbývající dva. Vstupem do goniometrické funkce je tak velikost úhlu. Výstupem je poměr nějakých dvou stran. Sinus a kvadranty
Stupně
Radiány
sin (x)
0°
0
0
90°
π/2
1
180°
π
0
270°
3π/2
−1
Historie goniometrie
Jejím průkopníkem se stal Aristarchos ze Samu, který studoval vzdálenosti Slunce a Měsíce od Země. Dále v budování goniometrie pokračovali vědci z Indie a Arábie, kteří věnovali úsilí spíše kalkulativním problémům a aritmetickým algoritmům.
Kolik je sin 120 : Hodnoty sinus na jednotkové kružnici
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Kde se dají použít goniometrické funkce? Weitere Antworten – Kdy se používají goniometrické funkce
Goniometrické funkce (nebo též trigonometrické funkce) je skupina funkcí, které dávají do vztahu úhel v pravoúhlém trojúhelníku a poměr dvou jeho stran. Goniometrické funkce mají široké využití v geometrii a mnoho praktických aplikací (například v navigaci, nebeské mechanice či geodézii).Jako goniometrické funkce se v matematice nazývá skupina šesti funkcí velikosti úhlu používaných například při zkoumání trojúhelníků a periodických jevů.Druhou souřadnici bodu jednotkové kružnice na koncovém rameni orientovaného úhlu v základní poloze nazýváme sinus a jeho první souřadnici nazveme kosinus . Používáme značení , . Je tedy , , pro každé .
Jak poznat síň cos TG : Goniometrické funkce a pravoúhlý trojúhelník
Kolik je síň 0
Sinus a kvadranty
Kolik je cos 0 : Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0. Pro α z ⟨π/2,π⟩ definujeme sin(α) = sin(π − α) a cos(α) = −cos(π − α). Pro α z ⟨π,2π⟩ definujeme sin(α) = −sin(α − π) a cos(α) = −cos(2π − α).
Goniometrické funkce (nebo též trigonometrické funkce) je skupina funkcí, které dávají do vztahu úhel v pravoúhlém trojúhelníku a poměr dvou jeho stran. Goniometrické funkce mají široké využití v geometrii a mnoho praktických aplikací (například v navigaci, nebeské mechanice či geodézii).
Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.
Kolik je síň 120
Hodnoty sinus na jednotkové kružnici
Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.sin(90) = sin(2.035rad) = 0.8939.
Goniometrické funkce, jako jsou sinus, kosinus, tangens a cotangens, jsou základními nástroji pro popis vztahů mezi úhly a délkami stran v pravoúhlém trojúhelníku. Tyto funkce se používají k výpočtu poměrů mezi délkami stran trojúhelníka a příslušnými úhly.
Kolik je síň 180 : Sinus a kvadranty
Co to je síň : Sinus je goniometrická funkce nějakého úhlu. Zapisuje se jako sin θ, kde θ je velikost úhlu. Pro ostré úhly je definována v pravoúhlém trojúhelníku jako poměr protilehlé odvěsny a přepony (nejdelší strany). Definici lze konzistentně rozšířit jak na všechna reálná čísla, tak i do oboru komplexních čísel.
Jak použít goniometrické funkce
Všechny goniometrické funkce nám ukazují vztah mezi nějakým úhlem v trojúhelníku a poměrem délek dvou stran. Zpravidla se pak nejedná o pravý úhel, ale o ty zbývající dva. Vstupem do goniometrické funkce je tak velikost úhlu. Výstupem je poměr nějakých dvou stran.
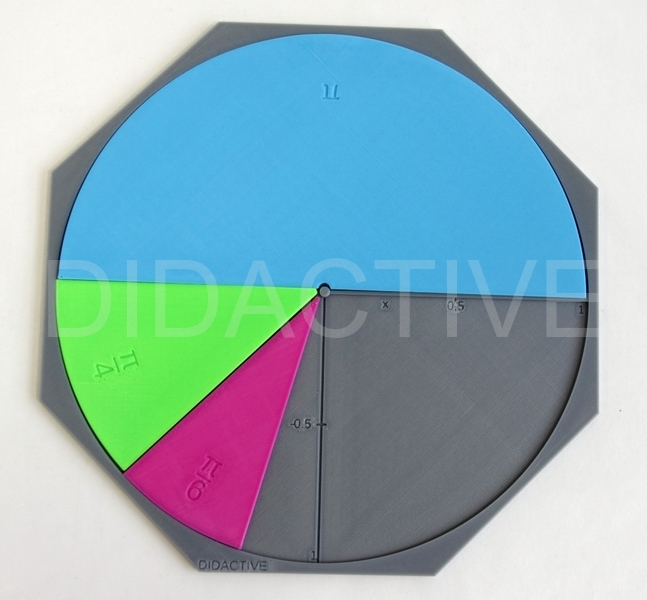
Sinus a kvadranty
Historie goniometrie
Jejím průkopníkem se stal Aristarchos ze Samu, který studoval vzdálenosti Slunce a Měsíce od Země. Dále v budování goniometrie pokračovali vědci z Indie a Arábie, kteří věnovali úsilí spíše kalkulativním problémům a aritmetickým algoritmům.
Kolik je sin 120 : Hodnoty sinus na jednotkové kružnici