Střed kružnice: Umístěte bod kružítka na jeden z bodů obvodu a nakreslete oblouk. Místo, kde se protíná s jiným bodem na obvodu, je váš druhý bod. Umístěte bod kompasu na tento druhý bod a nakreslete další oblouk. Místo, kde se protíná s dalším bodem na obvodu, je váš třetí bod.S kompasem nakreslete oblouk ze středu kruhu do bodu "A" a také oblouk do bodu "B". Pomocí pravítka přenesete střed kompasu na jeden z těchto bodů. Nakreslete další oblouk z bodu "A" až kde se protíná s obloukem z bodu "B". Místo protínání oblouků je střed kruhu.Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku. Máme trojúhelník ABC. Průsečík os o1 a o2 je střed S kružnice opsané k. Tuto kružnici sestrojíme, její poloměr je dán vzdáleností středu S a libovolného vrcholu.
Co to jsou soustředné kružnice : Kružnice a přímka nemají žádný společný bod. Dvě kružnice, které nemají společný střed, mohou mít společné právě dva body, právě jeden bod, nebo nemají žádný společný bod. Dvě kružnice, které mají společný střed, se nazývají soustředné.
Jak najít střed kružnice opsané
Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.
Jak zjistit zda bod leží na kružnici : 1) Vzhledem k tomu, že známe souřadnice středu kružnice a poloměr, stačí sestavit středovou rovnici kružnice: k: (x-1)^2+(y-2)^2=4 (nulové body jsou x-ové a -yové souřadnice středu, 4 je poloměr^2. Poté stačí obrázek a je vidět, že K je vnitřním bodem a M leží na kružnici.
Úhel, jehož vrcholem je střed O kružnice a jehož ramena procházejí krajními body oblouku AB kružnice k, se nazývá středový úhel příslušný k oblouku AB, který v tomto úhlu leží. Velikost středového úhlu je rovna dvojnásobku velikosti obvodového úhlu příslušného k témuž oblouku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.
Kde leží střed kružnice vepsané trojúhelníku
Střed kružnice vepsané leží na průsečíků os úhlů (je stejně daleko od všech stran trojúhelníku). Poloměr kružnice vepsané určíme pomocí kolmice na libovolnou stranu trojúhelníku procházející středem. Vzdálenost paty této kolmice od středu představuje poloměr kružnice vepsané.SEČNA KRUŽNICE je přímka, která má s kružnicí společné právě dva různé body.Thaletova věta je matematická věta o velikosti úhlů trojúhelníků vytvořených nad průměrem kružnice. Je pojmenována po Thalétovi z Milétu, který ji jako první dokázal. Kružnice, která je součástí konstrukce Thaletovy věty, bývá označována jako Thaletova kružnice. Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.
Jak zjistit Polomer Kruznice Vepsane : Střed kružnice vepsané leží na průsečíků os úhlů (je stejně daleko od všech stran trojúhelníku). Poloměr kružnice vepsané určíme pomocí kolmice na libovolnou stranu trojúhelníku procházející středem.
Jak poznat že body leží na přímce : Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Jak poznat že bod leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC. Velikost středového úhlu ω se rovná dvojnásobku velikosti obvodového úhlu φ příslušného ke stejnému oblouku, ω = 2 ⋅ φ \omega = 2\cdot\varphi ω=2⋅φ.umime.to/F4K
plný úhel
úhel o velikosti 360°
přímý úhel
úhel o velikosti 180°
pravý úhel
úhel o velikosti 90°
ostrý úhel
úhel menší než 90°
tupý úhel
úhel větší než 90° a menší než 180°
Co je to těžnice : Těžnice je úsečka spojující vrchol trojúhelníku se středem jeho protější stany. Příkladem v ABC je težnice ta, která je úsečkou ASa. Obdobně tak existují těžnice ke stranám b, c. Každý trojúhelník má tedy tři těžnice.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Kde lezi střed kružnice? Weitere Antworten – Jak najít střed v kružnici
Střed kružnice: Umístěte bod kružítka na jeden z bodů obvodu a nakreslete oblouk. Místo, kde se protíná s jiným bodem na obvodu, je váš druhý bod. Umístěte bod kompasu na tento druhý bod a nakreslete další oblouk. Místo, kde se protíná s dalším bodem na obvodu, je váš třetí bod.S kompasem nakreslete oblouk ze středu kruhu do bodu "A" a také oblouk do bodu "B". Pomocí pravítka přenesete střed kompasu na jeden z těchto bodů. Nakreslete další oblouk z bodu "A" až kde se protíná s obloukem z bodu "B". Místo protínání oblouků je střed kruhu.Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku. Máme trojúhelník ABC. Průsečík os o1 a o2 je střed S kružnice opsané k. Tuto kružnici sestrojíme, její poloměr je dán vzdáleností středu S a libovolného vrcholu.
Co to jsou soustředné kružnice : Kružnice a přímka nemají žádný společný bod. Dvě kružnice, které nemají společný střed, mohou mít společné právě dva body, právě jeden bod, nebo nemají žádný společný bod. Dvě kružnice, které mají společný střed, se nazývají soustředné.
Jak najít střed kružnice opsané
Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.
Jak zjistit zda bod leží na kružnici : 1) Vzhledem k tomu, že známe souřadnice středu kružnice a poloměr, stačí sestavit středovou rovnici kružnice: k: (x-1)^2+(y-2)^2=4 (nulové body jsou x-ové a -yové souřadnice středu, 4 je poloměr^2. Poté stačí obrázek a je vidět, že K je vnitřním bodem a M leží na kružnici.
Úhel, jehož vrcholem je střed O kružnice a jehož ramena procházejí krajními body oblouku AB kružnice k, se nazývá středový úhel příslušný k oblouku AB, který v tomto úhlu leží. Velikost středového úhlu je rovna dvojnásobku velikosti obvodového úhlu příslušného k témuž oblouku.
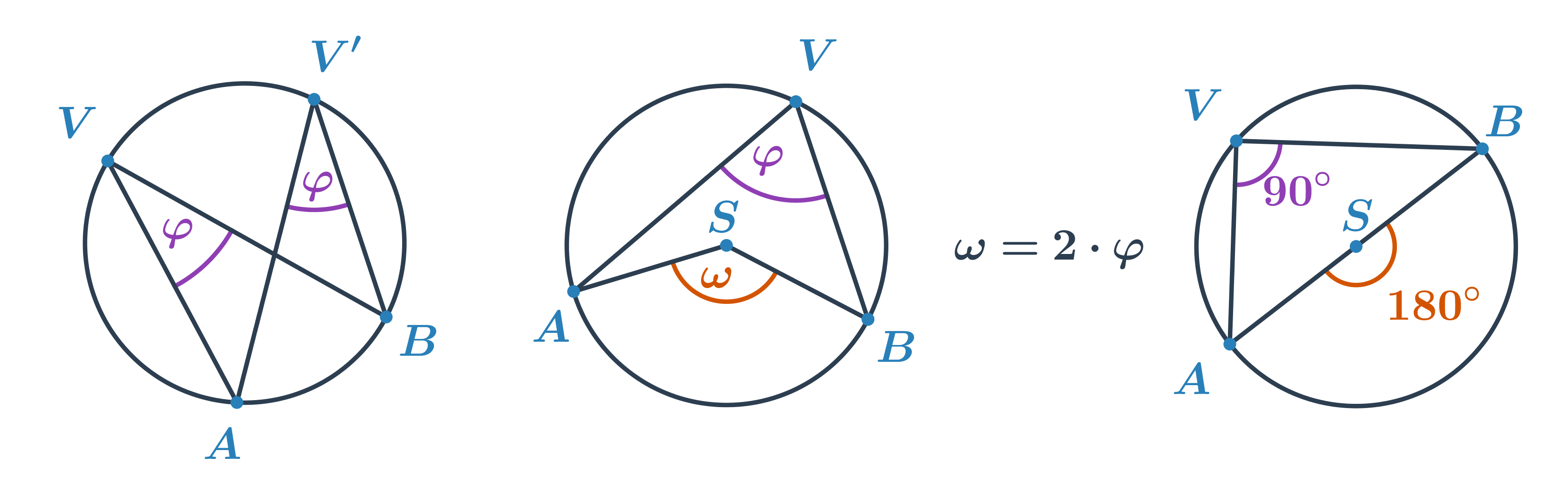
Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.
Kde leží střed kružnice vepsané trojúhelníku
Střed kružnice vepsané leží na průsečíků os úhlů (je stejně daleko od všech stran trojúhelníku). Poloměr kružnice vepsané určíme pomocí kolmice na libovolnou stranu trojúhelníku procházející středem. Vzdálenost paty této kolmice od středu představuje poloměr kružnice vepsané.SEČNA KRUŽNICE je přímka, která má s kružnicí společné právě dva různé body.Thaletova věta je matematická věta o velikosti úhlů trojúhelníků vytvořených nad průměrem kružnice. Je pojmenována po Thalétovi z Milétu, který ji jako první dokázal. Kružnice, která je součástí konstrukce Thaletovy věty, bývá označována jako Thaletova kružnice.
Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.
Jak zjistit Polomer Kruznice Vepsane : Střed kružnice vepsané leží na průsečíků os úhlů (je stejně daleko od všech stran trojúhelníku). Poloměr kružnice vepsané určíme pomocí kolmice na libovolnou stranu trojúhelníku procházející středem.
Jak poznat že body leží na přímce : Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Jak poznat že bod leží na přímce
Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC.
Velikost středového úhlu ω se rovná dvojnásobku velikosti obvodového úhlu φ příslušného ke stejnému oblouku, ω = 2 ⋅ φ \omega = 2\cdot\varphi ω=2⋅φ.umime.to/F4K
Co je to těžnice : Těžnice je úsečka spojující vrchol trojúhelníku se středem jeho protější stany. Příkladem v ABC je težnice ta, která je úsečkou ASa. Obdobně tak existují těžnice ke stranám b, c. Každý trojúhelník má tedy tři těžnice.