Antwort Jak zni věta SUS? Weitere Antworten – Jak zní věta SUS

Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení. Je-li poměr podobnosti k ˂ 1, jedná se o zmenšení.Velikost zadaného úhlu je menší než 180°. Věta usu Trojúhelník lze sestrojit podle věty usu, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. Věta Ssu Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich.

Co je podobnost trojúhelníku : VĚTA sus Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.

Co znamená věta SSS

Věta SSS: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné.

Jaký úhel svírá trojúhelník : Věta sus — v trojúhelníku jsou dány délky dvou stran a velikost úhlu, který svírají (menší než 180°).

Zobrazení f v rovině je podobné zobrazení, jestliže existuje číslo k > 0, že pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |X'Y'|=k\cdot |XY|. Podobné zobrazení se také nazývá podobnost. Číslo k se nazývá koeficient podobnosti.

Podobnost v rovině

Například všechny kružnice, čtverce a rovnostranné trojúhelníky si jsou podobné. Naopak elipsy si podobné být nemusí, stejně tak jako hyperboly.

Jak narýsovat trojúhelník podle věty sus

Věta SUS: Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu jimi sevřeným, pak jsou shodné.ROZBOR:

1. Sestrojíme úsečku AB o velikosti 8 cm.
2. Z bodu A sestrojíme oblouk kružnice k1 o poloměru 6 cm (2/3 délky těžnice ta)
3. Z bodu B sestrojíme oblouk kružnice k2 o poloměru 4 cm (2/3 délky těžnice tb)
4. Průsečík oblouků označíme T.
5. Sestrojíme polopřímku AT a na ní úsečku ASa délky ta.

Definice: Zobrazení v rovině se nazývá podobným zobrazením (podobností), jestliže každé úsečce AB přiřazuje úsečku A´B´ pro jejíž velikost platí . Koeficient k nazýváme poměr podobnosti.

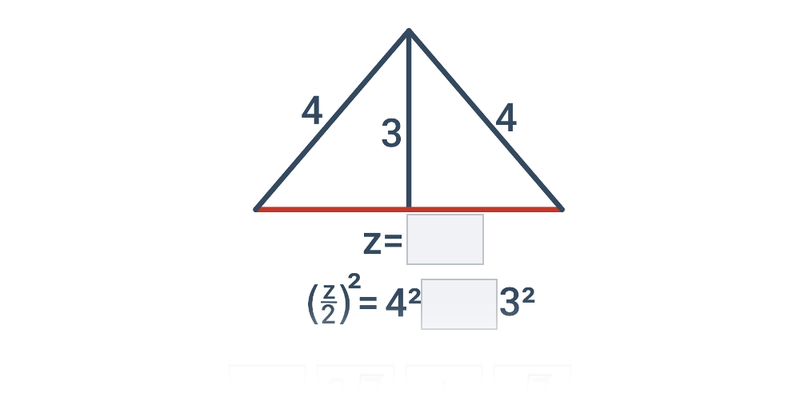
Strana, která není shodná s rameny, se nazývá základna. Vrchol naproti základně se nazývá hlavní vrchol.

Jak Narysovat usu : Věta USU: Pokud se dva trojúhelníky shodují v jedné straně a v obou úhlech k této straně přilehlých, pak jsou shodné.

Co je to věta usu : Věta usu: Shodují-li se dva trojúhelníky ve straně a v obou přilehlých úhlech, jsou shodné.

Co vime o trojúhelníku

Nejnápadnější pravidlo: Trojúhelník má tolik shodných úhlů, kolik má shodných stran. Navíc víme, kde shodné úhly leží. U rovnoramenného trojúhelníka jsou shodné strany a, b a shodné úhly α a β (úhly ležící proti shodným stranám) ⇒ proti shodným stranám leží shodné úhly.

Součet všech vnitřních úhlů je v každém trojúhelníku 180°. Součet vnitřního a příslušného vnějšího úhlu je 180°. Součet dvou vnitřních úhlů se rovná vnějšímu úhlu u zbývajícího vrcholu.Rovina je v matematice dvourozměrný geometrický útvar, který si lze představit jako neomezenou dokonale rovnou plochu. Algebraicky vyjádřeno, jde o množinu bodů izomorfní s dvoudimenzionálním lineárním prostorem. Jinak řečeno jde o dvoudimenzionální afinní prostor.

Jak narýsovat trojúhelník podle věty usu : Věta USU: Pokud se dva trojúhelníky shodují v jedné straně a v obou úhlech k této straně přilehlých, pak jsou shodné.