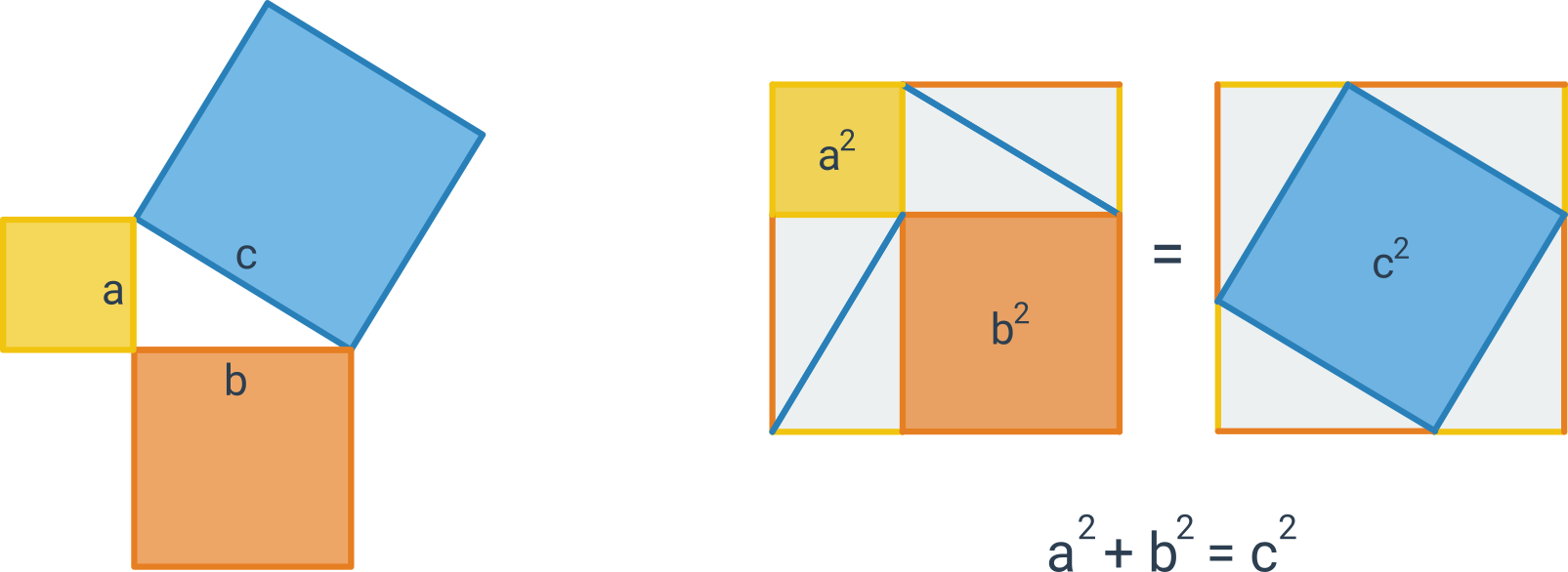
Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.Platí i věta obrácená k Pythagorově větě
Jsou-li a, b, c délky stran trojúhelníku a platí-li c2 = a2 + b2, pak je trojúhelník pravoúhlý a c je délka jeho přepony.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak se počítá výška trojúhelníku Pythagorova věta : Vypocitejte jeho vysku. Jak se pocita to cviceni To je pythagorova věta – c^2=a^2+b^2, kde c je rameno, a je výška a b polovina základny (výška v rovnoramenném trojúhelníku půlí základnu).
Proč funguje Pythagorova věta
Pythagorova věta popisuje vztah mezi délkami stran libovolného pravoúhlého trojúhelníku v euklidovské rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran. Věta zní: Součet obsahů čtverců nad oběma odvěsnami se rovná obsahu čtverce nad přeponou.
Jak se pocita Odvesna vzorec : Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Věta pojmenovaná po řeckém matematikovi Pythagorovi byla formulovaná již dříve Babyloňany a Číňany. Na babylonských hliněných tabulkách z 18. století před n. l se objevil součet 32 + 42 = 52. Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Jak poznat Přeponu v trojúhelníku
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.Umožňuje dopočítat délku třetí strany takového trojúhelníku, pokud jsou známy délky dvou zbývajících stran. Věta zní: Obsah čtverce sestrojeného nad přeponou libovolného pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami (dvěma kratšími stranami).Výška v trojúhelníku je vlastně vzdálenost vrcholu od protější strany. Vzdálenost se měří vždy na kolmici, proto je to kolmice spuštěná z vrcholu na protější stranu. Výšky se rýsují celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice procházela právě bodem C. Výšku můžeme vést z každého vrcholu trojúhelníka. Všechny výšky se pak protínají v bodě, které se nazývá průsečík výšek.
Jak zni Kosinová věta : Kosinová věta zní: C na druhou se rovná A na druhou plus B na druhou, minus 2AB krát kosinus théty.
Kdo vymyslel Pythagorovu větu :
Pythagoras
Úmrtí
Desetiletí do 490 př. n. l. Metapontum
Povolání
matematik, filozof, politik, spisovatel, muzikolog a hudební teoretik
Témata
geometrie, matematika, etika, politika, filozofie, astronomie, hudba a metafyzika
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.
Věta byla pojmenována podle řeckého filosofa a matematika Pythagora, jenž ji v 6. století př. n. l. objevil pro Evropu, resp. starověkou Indii.
Kdy se používá Pythagorova věta : Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak zní Pythagorova věta? Weitere Antworten – Jak se pocita Pythagora
Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.Platí i věta obrácená k Pythagorově větě
Jsou-li a, b, c délky stran trojúhelníku a platí-li c2 = a2 + b2, pak je trojúhelník pravoúhlý a c je délka jeho přepony.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
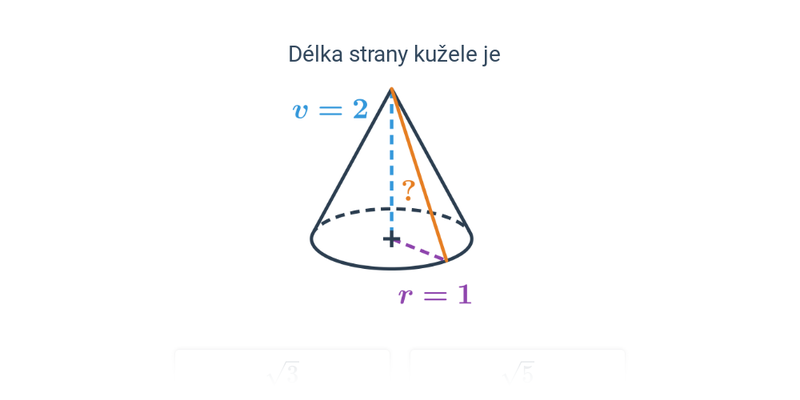
Jak se počítá výška trojúhelníku Pythagorova věta : Vypocitejte jeho vysku. Jak se pocita to cviceni To je pythagorova věta – c^2=a^2+b^2, kde c je rameno, a je výška a b polovina základny (výška v rovnoramenném trojúhelníku půlí základnu).
Proč funguje Pythagorova věta
Pythagorova věta popisuje vztah mezi délkami stran libovolného pravoúhlého trojúhelníku v euklidovské rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran. Věta zní: Součet obsahů čtverců nad oběma odvěsnami se rovná obsahu čtverce nad přeponou.
Jak se pocita Odvesna vzorec : Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Věta pojmenovaná po řeckém matematikovi Pythagorovi byla formulovaná již dříve Babyloňany a Číňany. Na babylonských hliněných tabulkách z 18. století před n. l se objevil součet 32 + 42 = 52.
Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Jak poznat Přeponu v trojúhelníku
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.Umožňuje dopočítat délku třetí strany takového trojúhelníku, pokud jsou známy délky dvou zbývajících stran. Věta zní: Obsah čtverce sestrojeného nad přeponou libovolného pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami (dvěma kratšími stranami).Výška v trojúhelníku je vlastně vzdálenost vrcholu od protější strany. Vzdálenost se měří vždy na kolmici, proto je to kolmice spuštěná z vrcholu na protější stranu.
Výšky se rýsují celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice procházela právě bodem C. Výšku můžeme vést z každého vrcholu trojúhelníka. Všechny výšky se pak protínají v bodě, které se nazývá průsečík výšek.
Jak zni Kosinová věta : Kosinová věta zní: C na druhou se rovná A na druhou plus B na druhou, minus 2AB krát kosinus théty.
Kdo vymyslel Pythagorovu větu :
Jak poznat Přeponu a Odvěsnu
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.
Věta byla pojmenována podle řeckého filosofa a matematika Pythagora, jenž ji v 6. století př. n. l. objevil pro Evropu, resp. starověkou Indii.
Kdy se používá Pythagorova věta : Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .