Podobné zobrazení, je takové zobrazení, ve kterém pro vzdálenost dvou obrazů X´, Y´ libovolných dvou bodů (vzorů) X, Y platí: |X´Y´|=k·|XY|, kde k je libovolné kladné reálné číslo různé od nuly.ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm. Určete obvod podobného trojúhelníka XYZ, je-li poměr podobnosti 0,01.Podobné zobrazení s koeficientem podobnosti k=1 je shodné zobrazení. Každé podobné zobrazení je prosté. Obdobně jako u shodného zobrazení v každém podobném zobrazení s koeficientem podobnosti k platí: Obrazem každé úsečky AB je úsečka A'B', pro kterou platí |A'B'|=k\cdot |AB|.
Co je to věta SSS : Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.
Co to je koeficient podobnosti
Přesněji řečeno, útvary jsou podobné, pokud jeden můžeme získat z druhého kombinací rovnoměrného zmenšení či zvětšení a následným posunutím, otočením nebo překlopením. Podobnost zachovává velikost úhlů a poměr délek. Poměr délek odpovídajících úseček v obou útvarech se nazývá koeficient podobnosti.
Jak zapsat shodnost Trojuhelniku : Shodují-li se dva trojúhelníky ve všech třech odpovídajících si stranách, pak jsou shodné. Protože |AB| = |XY|, je možné trojúhelník XYZ přemístit tak, aby bod X splynul s bodem A a bod Y s bodem B. Protože |XZ| = b a |YZ| = a, leží bod Z na kružnicích c(A,b) a d(B,e).
Definice: Zobrazení v rovině se nazývá podobným zobrazením (podobností), jestliže každé úsečce AB přiřazuje úsečku A´B´ pro jejíž velikost platí . Koeficient k nazýváme poměr podobnosti. Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).
Co to je věta SUS
Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).
Věta „sss“ Shodují-li se dva trojúhelníky ve všech třech odpovídajících si stranách, pak jsou shodné.
Věta „sus“ Shodují-li se dva trojúhelníky ve dvou stranách a úhlu jimi sevřeném, jsou shodné.
Věta „usu“ Shodují-li se dva trojúhelníky v jedné straně a v obou úhlech k ní přilehlých, jsou shodné.
Věta „Ssu“
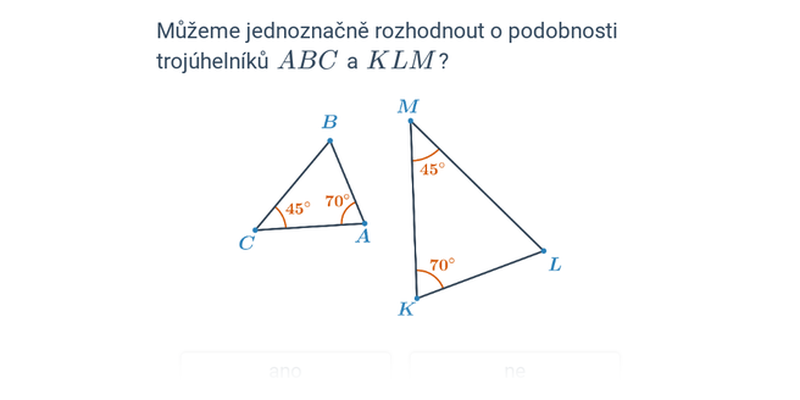
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení. Těžiště se vždy nachází uvnitř trojúhelníku.
To znamená, že dvě třetiny délky těžnice jsou na jedné straně od těžiště a zbývající jedna třetina na další straně. Delší část těžnice je vždy směrem „k vrcholu“ trojúhelníku.
Co je to přímá a nepřímá shodnost : Přímá a nepřímá shodnost
Shodnost zachovávající orientaci se nazývá přímá neboli přemístění. Shodnost měnící orientaci se nazývá nepřímá. Posunutí a otočení (a tedy i středová souměrnost) jsou přímé shodnosti (přemístění), zachovávají orientaci. (Posunuté) osové souměrnosti jsou nepřímé shodnosti, mění orientaci.
Jak narýsovat trojúhelník podle věty SSU : Velikost zadaného úhlu je menší než 180°. Věta usu Trojúhelník lze sestrojit podle věty usu, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. Věta Ssu Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich.
Jak zapsat shodnost trojúhelníku
Shodují-li se dva trojúhelníky ve všech třech odpovídajících si stranách, pak jsou shodné. Protože |AB| = |XY|, je možné trojúhelník XYZ přemístit tak, aby bod X splynul s bodem A a bod Y s bodem B. Protože |XZ| = b a |YZ| = a, leží bod Z na kružnicích c(A,b) a d(B,e). Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny.
Co je stred trojúhelníku : Střed kružnice opsané trojúhelníku je průsečík os stran trojúhelníku, poloměr se rovná vzdálenosti středu od libovolného vrcholu.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak zapsat podobnost? Weitere Antworten – Jak se zapisuje podobnost
Podobné zobrazení, je takové zobrazení, ve kterém pro vzdálenost dvou obrazů X´, Y´ libovolných dvou bodů (vzorů) X, Y platí: |X´Y´|=k·|XY|, kde k je libovolné kladné reálné číslo různé od nuly.ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm. Určete obvod podobného trojúhelníka XYZ, je-li poměr podobnosti 0,01.Podobné zobrazení s koeficientem podobnosti k=1 je shodné zobrazení. Každé podobné zobrazení je prosté. Obdobně jako u shodného zobrazení v každém podobném zobrazení s koeficientem podobnosti k platí: Obrazem každé úsečky AB je úsečka A'B', pro kterou platí |A'B'|=k\cdot |AB|.
Co je to věta SSS : Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.
Co to je koeficient podobnosti
Přesněji řečeno, útvary jsou podobné, pokud jeden můžeme získat z druhého kombinací rovnoměrného zmenšení či zvětšení a následným posunutím, otočením nebo překlopením. Podobnost zachovává velikost úhlů a poměr délek. Poměr délek odpovídajících úseček v obou útvarech se nazývá koeficient podobnosti.
Jak zapsat shodnost Trojuhelniku : Shodují-li se dva trojúhelníky ve všech třech odpovídajících si stranách, pak jsou shodné. Protože |AB| = |XY|, je možné trojúhelník XYZ přemístit tak, aby bod X splynul s bodem A a bod Y s bodem B. Protože |XZ| = b a |YZ| = a, leží bod Z na kružnicích c(A,b) a d(B,e).
Definice: Zobrazení v rovině se nazývá podobným zobrazením (podobností), jestliže každé úsečce AB přiřazuje úsečku A´B´ pro jejíž velikost platí . Koeficient k nazýváme poměr podobnosti.
Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).
Co to je věta SUS
Pokud se dva trojúhelníky shodují ve dvou stranách a úhlu, který strany svírají, jsou shodné (věta sus).
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení.
Těžiště se vždy nachází uvnitř trojúhelníku.
To znamená, že dvě třetiny délky těžnice jsou na jedné straně od těžiště a zbývající jedna třetina na další straně. Delší část těžnice je vždy směrem „k vrcholu“ trojúhelníku.
Co je to přímá a nepřímá shodnost : Přímá a nepřímá shodnost
Shodnost zachovávající orientaci se nazývá přímá neboli přemístění. Shodnost měnící orientaci se nazývá nepřímá. Posunutí a otočení (a tedy i středová souměrnost) jsou přímé shodnosti (přemístění), zachovávají orientaci. (Posunuté) osové souměrnosti jsou nepřímé shodnosti, mění orientaci.
Jak narýsovat trojúhelník podle věty SSU : Velikost zadaného úhlu je menší než 180°. Věta usu Trojúhelník lze sestrojit podle věty usu, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. Věta Ssu Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich.
Jak zapsat shodnost trojúhelníku
Shodují-li se dva trojúhelníky ve všech třech odpovídajících si stranách, pak jsou shodné. Protože |AB| = |XY|, je možné trojúhelník XYZ přemístit tak, aby bod X splynul s bodem A a bod Y s bodem B. Protože |XZ| = b a |YZ| = a, leží bod Z na kružnicích c(A,b) a d(B,e).
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny.
Co je stred trojúhelníku : Střed kružnice opsané trojúhelníku je průsečík os stran trojúhelníku, poloměr se rovná vzdálenosti středu od libovolného vrcholu.