Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.umime.to/FV2
Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak se počítá Odvěsna v pravoúhlém trojúhelníku : V pravoúhlém trojúhelníku je přepona nejdelší stranou. "Protilehlá odvěsna" je strana naproti zadanému úhlu a "přilehlá odvěsna" je strana vedle daného úhlu.
Jak zjistit třetí stranu trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Co platí v pravoúhlém trojúhelníku : V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 . Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
Jak zjistit jednu stranu trojúhelníku
Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.Goniometrické funkce a pravoúhlý trojúhelník
Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny.
Jak spočítat 3 stranu trojúhelníku : Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak zjistit Preponu : Pythagorova věta
c2 = a2 + b2 – tedy:
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených nad jeho odvěsnami.
Jak se pocita tg
Existují ještě dvě další goniometrické funkce, tangens a kotangens. Hlavní rozdíl oproti předchozím goniometrickým funkcím je ten, že tangens a kotangens pracuje pouze s odvěsnami, nepracuje s přeponou. Tangens úhlu α se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny.
X [º]
X [rad]
cos(2x)
1
0,0175
0,9994
2
0,0349
0,9976
3
0,0524
0,9945
4
0,0698
0,9903
Hodnoty sinus na jednotkové kružnici
x (úhel)
30°
π/6
1/12
150°
5π/6
5/12
45°
π/4
1/8
135°
3π/4
3/8
Jak se pocita síň cos tg : Goniometrické funkce a pravoúhlý trojúhelník
Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Antwort Jak vypočítat třetí stranu pravoúhlého trojúhelníku? Weitere Antworten – Jak vypočítat strany pravoúhlého trojúhelníku
Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.umime.to/FV2
Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
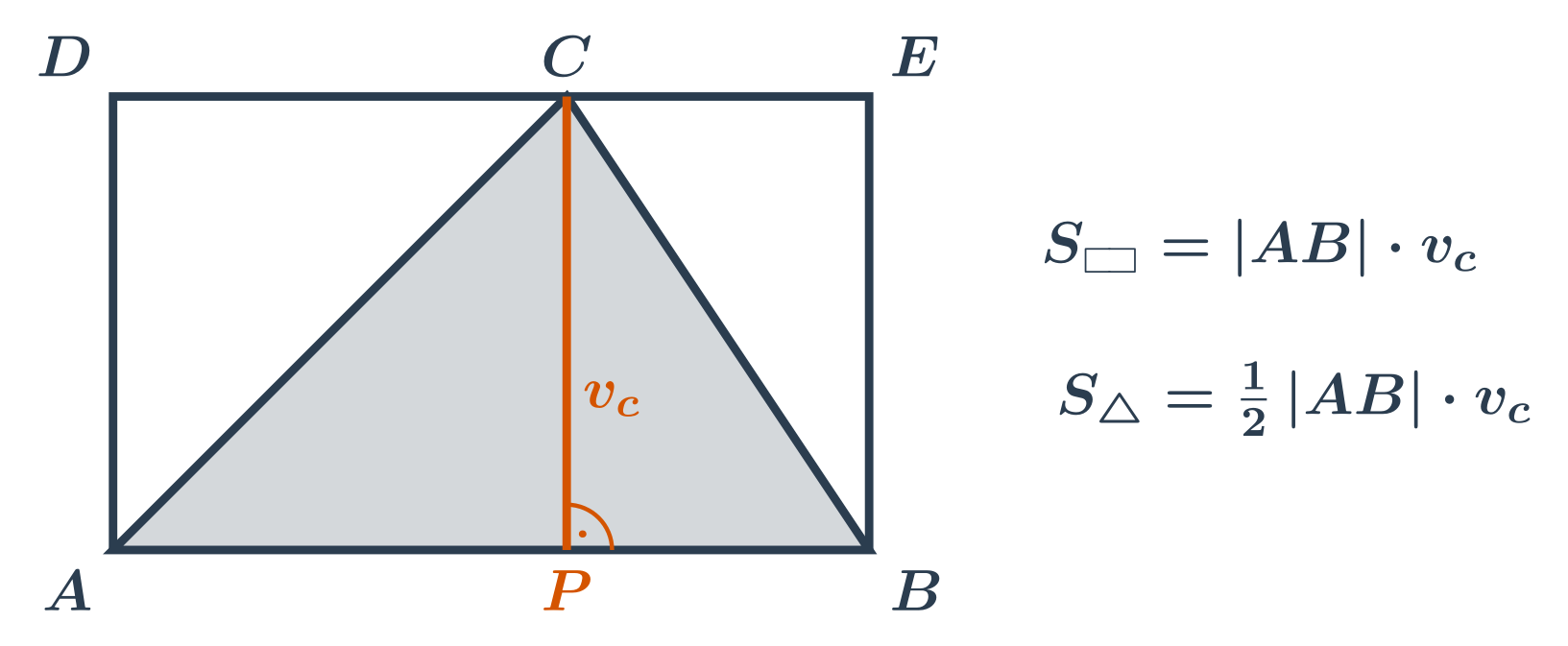
Jak se počítá Odvěsna v pravoúhlém trojúhelníku : V pravoúhlém trojúhelníku je přepona nejdelší stranou. "Protilehlá odvěsna" je strana naproti zadanému úhlu a "přilehlá odvěsna" je strana vedle daného úhlu.
Jak zjistit třetí stranu trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Co platí v pravoúhlém trojúhelníku : V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
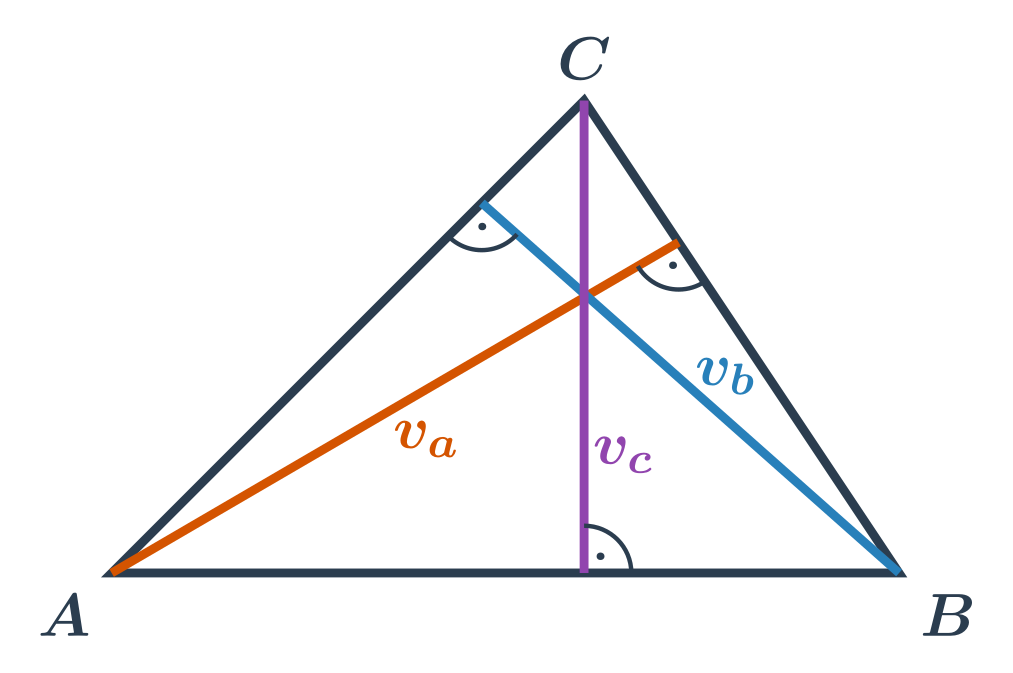
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
Jak zjistit jednu stranu trojúhelníku
Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.Goniometrické funkce a pravoúhlý trojúhelník
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny.
Jak spočítat 3 stranu trojúhelníku : Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak zjistit Preponu : Pythagorova věta
Jak se pocita tg
Existují ještě dvě další goniometrické funkce, tangens a kotangens. Hlavní rozdíl oproti předchozím goniometrickým funkcím je ten, že tangens a kotangens pracuje pouze s odvěsnami, nepracuje s přeponou. Tangens úhlu α se rovná poměru délky protilehlé odvěsny ku délce přilehlé odvěsny.

Hodnoty sinus na jednotkové kružnici
Jak se pocita síň cos tg : Goniometrické funkce a pravoúhlý trojúhelník