Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
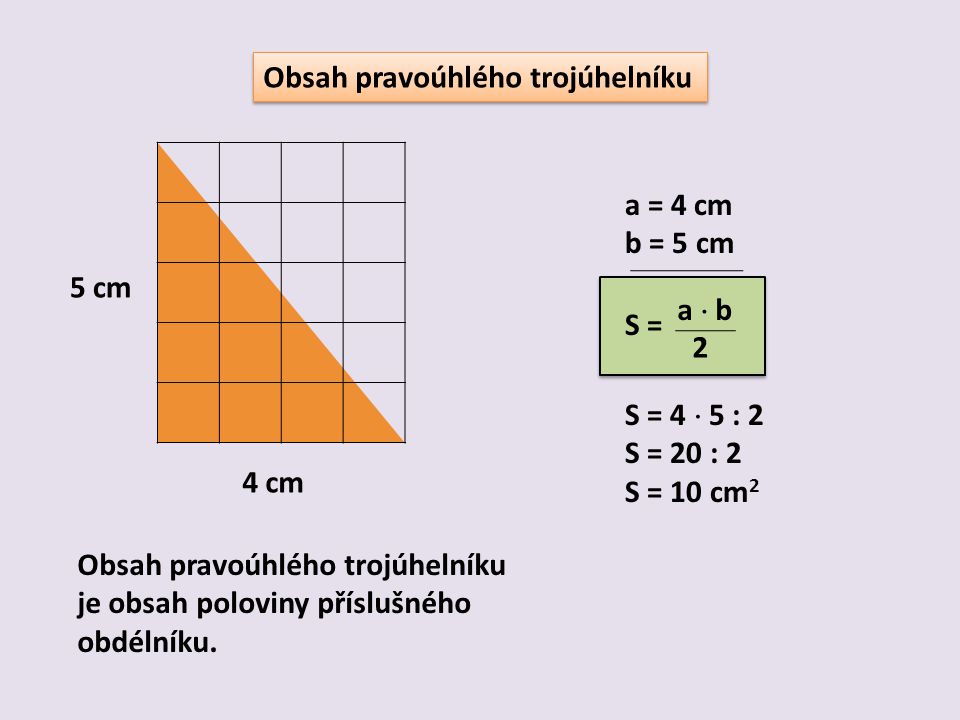
Jak se vypočítá obsah pravoúhlého trojúhelníku : Obsah pravoúhlého trojúhelníku
Vzorec by tedy vypadal takto: S △ = b ⋅ c 2 , kde b a c jsou délky odvěsen.
Jak zjistit jednu stranu trojúhelníku
Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.
Jak vypočítat poměr stran trojúhelníku : Při rozdělení v daném poměru musíme sečíst všechny členy poměru ( počet dílů) a ze známého celku vypočítat velikost jednoho dílu. Cv20/7 V trojúhelníku jsou délky stran v postupném poměru 5 : 7 : 9, nejdelší strana má 27 cm.
↑ ander: obsah čtverce získáš tak že umocníš délku jeho strany na druhou. Obráceně tedy získáš délku strany tak že obsah čtverce omocníš. Dva jsou tisíckrát jeden. Obsah trojúhelníku vypočítáme tak, že vynásobíme délku libovolné strany s výškou trojúhelníku, která je na tuto stranu kolmá, a to celé vydělíme dvěma. Pokud neznáte žádnou výšku, ale znáte délky všech stran trojúhelníku, můžete jeho obsah spočítat z Heronova vzorce.
Jak se počítá délka přepony
Vzorce: Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.Zjištění poměru stran
Vypočítejte vztah mezi šířkou (první číslo) a výškou (druhé číslo). Například: Obrázky s rozměry 1 600 x 900 pixelů nebo 3 200 x 1 800 pixelů mají poměr stran 16:9. Obrázky s rozměry 1 600 x 1 600 pixelů a 3 200 x 3 200 pixelů mají poměr stran 1:1. Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Jak vypočítat stranu obdélníku z obsahu : Potřebujeme získat počet dílků, obdélník má 4 strany, z toho 2 mají počet dílků "3" a zbylé 2 mají počet dílků "2". Celkový počet dílků = 2×3 + 2×2 = 10. Obvod vydělíme počtem dílků a získáme hodnotu jednoho (60 : 10 = 6). Délka jedné strany je (počet dílků * hodnota jednoho dílku) 2 * 6 = 12 , 3 * 6 = 18.
Jaký je vzoreček pro obsah : Vzorec vypadá takto: S=va·a .
Na co je Heronuv vzorec
Heronův vzorec je vzorec pro výpočet obsahu obecného trojúhelníku (v eukleidovské rovině) pomocí délek jeho stran. Pokud 3 kladná čísla splňují trojúhelníkovou nerovnost, existuje v eukleidovské rovině (podle věty sss) až na polohu a orientaci jediný trojúhelník s těmito délkami stran. Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.
Jak vypočítat strany trojúhelníku : Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran:
Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Délka odvěsny a = c 2 − b 2 a = \sqrt{c^2-b^2} a=c2−b2 .
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak vypočítat stranu pravoúhlého trojúhelníku z obsahu? Weitere Antworten – Jak vypočítat strany pravoúhlého trojúhelníku
Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak se vypočítá obsah pravoúhlého trojúhelníku : Obsah pravoúhlého trojúhelníku
Vzorec by tedy vypadal takto: S △ = b ⋅ c 2 , kde b a c jsou délky odvěsen.
Jak zjistit jednu stranu trojúhelníku
Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.
Jak vypočítat poměr stran trojúhelníku : Při rozdělení v daném poměru musíme sečíst všechny členy poměru ( počet dílů) a ze známého celku vypočítat velikost jednoho dílu. Cv20/7 V trojúhelníku jsou délky stran v postupném poměru 5 : 7 : 9, nejdelší strana má 27 cm.
↑ ander: obsah čtverce získáš tak že umocníš délku jeho strany na druhou. Obráceně tedy získáš délku strany tak že obsah čtverce omocníš. Dva jsou tisíckrát jeden.
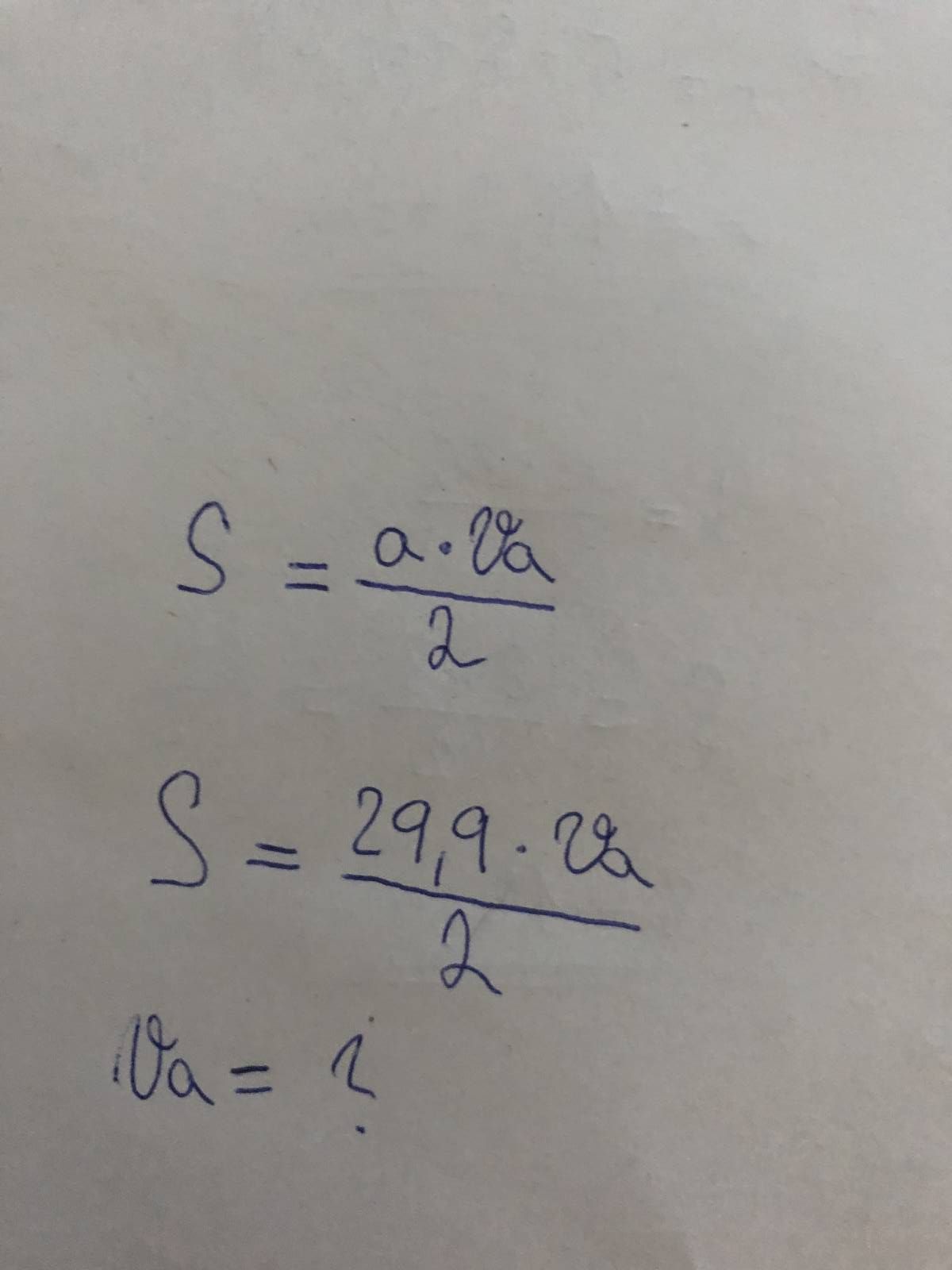
Obsah trojúhelníku vypočítáme tak, že vynásobíme délku libovolné strany s výškou trojúhelníku, která je na tuto stranu kolmá, a to celé vydělíme dvěma. Pokud neznáte žádnou výšku, ale znáte délky všech stran trojúhelníku, můžete jeho obsah spočítat z Heronova vzorce.
Jak se počítá délka přepony
Vzorce: Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.Zjištění poměru stran
Vypočítejte vztah mezi šířkou (první číslo) a výškou (druhé číslo). Například: Obrázky s rozměry 1 600 x 900 pixelů nebo 3 200 x 1 800 pixelů mají poměr stran 16:9. Obrázky s rozměry 1 600 x 1 600 pixelů a 3 200 x 3 200 pixelů mají poměr stran 1:1.
Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Jak vypočítat stranu obdélníku z obsahu : Potřebujeme získat počet dílků, obdélník má 4 strany, z toho 2 mají počet dílků "3" a zbylé 2 mají počet dílků "2". Celkový počet dílků = 2×3 + 2×2 = 10. Obvod vydělíme počtem dílků a získáme hodnotu jednoho (60 : 10 = 6). Délka jedné strany je (počet dílků * hodnota jednoho dílku) 2 * 6 = 12 , 3 * 6 = 18.
Jaký je vzoreček pro obsah : Vzorec vypadá takto: S=va·a .
Na co je Heronuv vzorec
Heronův vzorec je vzorec pro výpočet obsahu obecného trojúhelníku (v eukleidovské rovině) pomocí délek jeho stran. Pokud 3 kladná čísla splňují trojúhelníkovou nerovnost, existuje v eukleidovské rovině (podle věty sss) až na polohu a orientaci jediný trojúhelník s těmito délkami stran.
Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.
Jak vypočítat strany trojúhelníku : Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: