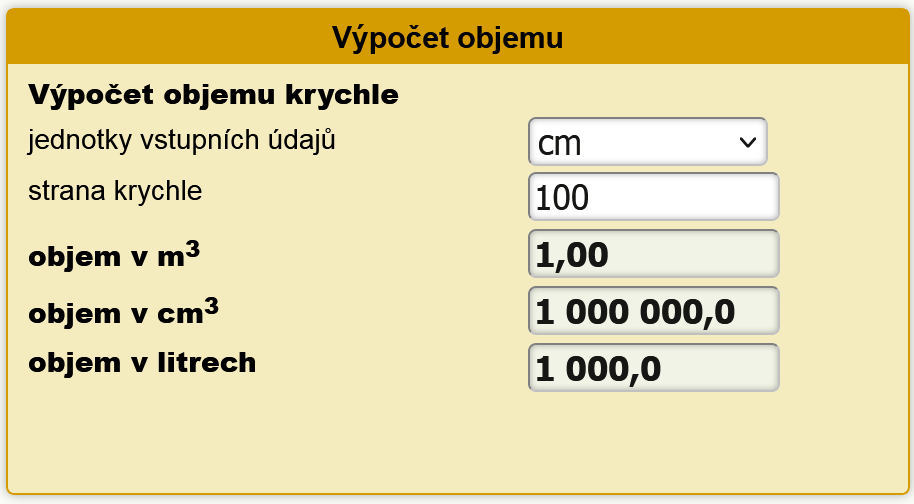
Krychle má šest stěn a všechny jsou tvořeny stejným čtvercem => je složena ze 6 čtverců. Každý z těchto čtverců má obsah S = a², proto lze vyjádřit obsah krychle vzorcem: S = 6 . a².
Jak vypočítat plášť krychle : Obsah pláště spočítáme jako součet obsahů stěn jehlanu, které tvoří plášť (tj. všechny stěny jehlanu kromě jeho podstavy).
Jak spočítat 3 stranu trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak se vypočítá strana kvádru : U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c). Výsledná hodnota je v objemových jednotkách.
Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku. Vzorec pro výpočet objemu místnosti je tedy: V = a * b * c, kde a je délka, b je šířka a c je výška místnosti. Například, pokud má místnost délku 5 metrů, šířku 4 metry a výšku 3 metry, objem místnosti bude V = 5 * 4 * 3 = 60 metrů krychlových.
Jaký je vzorec pro obsah válce
Vzorce pro výpočet objemu válce
Objem/obsah válce se spočítá jako plocha základny [S] × výška válce [v]. Plocha základny válce se spočítá z poloměru kružnice základny [r] jako: 3,14 (π) × r2. Celý vzorec pro výpočet objemu válce vypadá takto: [V] = π × r2 × v.Boční stěny hranolu tvoří plášť hranolu. Výškou hranolu je vzdálenost obou podstav. OBJEM hranolu vypočítáme jako součin obsahu podstavy (SP) a výšky hranolu (v). V = SP · v POVRCH hranolu je roven součtu obsahů obou podstav (SP) hranolu a obsahu pláště hranolu SPL (SPL = S1 + S2 + S3 + S4).Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c]. Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak vypočítat poměr stran trojúhelníku : Při rozdělení v daném poměru musíme sečíst všechny členy poměru ( počet dílů) a ze známého celku vypočítat velikost jednoho dílu. Cv20/7 V trojúhelníku jsou délky stran v postupném poměru 5 : 7 : 9, nejdelší strana má 27 cm.
Jak vypočítat jednu stranu obdélníku : Obvod vydělíme počtem dílků a získáme hodnotu jednoho (60 : 10 = 6). Délka jedné strany je (počet dílků * hodnota jednoho dílku) 2 * 6 = 12 , 3 * 6 = 18.
Jaké jsou rozměry kvádru
Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle. U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c). Výsledná hodnota je v objemových jednotkách.Objem válce je π r² v a jeho plocha se dá zjistit pomocí vzorce 2 π r v + 2 π r².
Jak vypočítat SP válce : Existuje i jednodušší vzorec: S = 2π. r . (r + v). Ten má velkou nevýhodu: dá se podle něj spočítat pouze povrch celého válce.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak vypočítat stranu krychle? Weitere Antworten – Jak se počítá strana krychle
Odvozené vzorce
umime.to/FV6
Krychle má šest stěn a všechny jsou tvořeny stejným čtvercem => je složena ze 6 čtverců. Každý z těchto čtverců má obsah S = a², proto lze vyjádřit obsah krychle vzorcem: S = 6 . a².
Jak vypočítat plášť krychle : Obsah pláště spočítáme jako součet obsahů stěn jehlanu, které tvoří plášť (tj. všechny stěny jehlanu kromě jeho podstavy).
Jak spočítat 3 stranu trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak se vypočítá strana kvádru : U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c). Výsledná hodnota je v objemových jednotkách.
Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Vzorec pro výpočet objemu místnosti je tedy: V = a * b * c, kde a je délka, b je šířka a c je výška místnosti. Například, pokud má místnost délku 5 metrů, šířku 4 metry a výšku 3 metry, objem místnosti bude V = 5 * 4 * 3 = 60 metrů krychlových.
Jaký je vzorec pro obsah válce
Vzorce pro výpočet objemu válce
Objem/obsah válce se spočítá jako plocha základny [S] × výška válce [v]. Plocha základny válce se spočítá z poloměru kružnice základny [r] jako: 3,14 (π) × r2. Celý vzorec pro výpočet objemu válce vypadá takto: [V] = π × r2 × v.Boční stěny hranolu tvoří plášť hranolu. Výškou hranolu je vzdálenost obou podstav. OBJEM hranolu vypočítáme jako součin obsahu podstavy (SP) a výšky hranolu (v). V = SP · v POVRCH hranolu je roven součtu obsahů obou podstav (SP) hranolu a obsahu pláště hranolu SPL (SPL = S1 + S2 + S3 + S4).Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak vypočítat poměr stran trojúhelníku : Při rozdělení v daném poměru musíme sečíst všechny členy poměru ( počet dílů) a ze známého celku vypočítat velikost jednoho dílu. Cv20/7 V trojúhelníku jsou délky stran v postupném poměru 5 : 7 : 9, nejdelší strana má 27 cm.
Jak vypočítat jednu stranu obdélníku : Obvod vydělíme počtem dílků a získáme hodnotu jednoho (60 : 10 = 6). Délka jedné strany je (počet dílků * hodnota jednoho dílku) 2 * 6 = 12 , 3 * 6 = 18.
Jaké jsou rozměry kvádru
Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle.
U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c). Výsledná hodnota je v objemových jednotkách.Objem válce je π r² v a jeho plocha se dá zjistit pomocí vzorce 2 π r v + 2 π r².
Jak vypočítat SP válce : Existuje i jednodušší vzorec: S = 2π. r . (r + v). Ten má velkou nevýhodu: dá se podle něj spočítat pouze povrch celého válce.