Kružnice opsaná trojúhelníku. Střed kružnice opsané trojúhelníku je průsečík os stran trojúhelníku, poloměr se rovná vzdálenosti středu od libovolného vrcholu.Obvod kružnice se spočítá jako 3,14 [π] x průměr kružnice [d], nebo 2 x 3,14 [π] x poloměr kružnice [r].Poloměr kružnice opsané je vzdálenost středu od libovolného vrcholu. Střed kružnice vepsané leží na průsečíků os úhlů (je stejně daleko od všech stran trojúhelníku). Poloměr kružnice vepsané určíme pomocí kolmice na libovolnou stranu trojúhelníku procházející středem.
Jak se dělá kružnice vepsaná a opsaná : Kružnice opsaná prochází všemi třemi vrcholy trojúhelníku, kružnice vepsaná se dotýká všech tří stran trojúhelníka (strany jsou tečnami kružnice). Obě kružnice jsou třemi vrcholy trojúhelníka jednoznačně určené.
Jak zjistit zda bod leží na kružnici
1) Vzhledem k tomu, že známe souřadnice středu kružnice a poloměr, stačí sestavit středovou rovnici kružnice: k: (x-1)^2+(y-2)^2=4 (nulové body jsou x-ové a -yové souřadnice středu, 4 je poloměr^2. Poté stačí obrázek a je vidět, že K je vnitřním bodem a M leží na kružnici.
Jak na kružnicí vepsanou : Sestrojíme osu o1 úhlu α. Sestrojíme osu o2 úhlu β. Průsečík os o1 a o2 je střed S kružnice vepsané k. Tuto kružnici sestrojíme, její poloměr je dán vzdáleností středu S a libovolné strany (určíme jej po sestrojení kolmice ze středu S na libovolnou stranu).
Kružnice vepsaná
Taková kružnice má střed Sv, poloměr d(Sv, AB) a nazývá se vepsaná, značíme kv. Body dotyku vepsané kružnice s jednotlivými stranami značíme Ta, Tb, Tc. Vzoreček pro výpočet obvodu kružnice je jednoduchý: Obvod kruhu o = 2 π (3,14) × poloměr r.
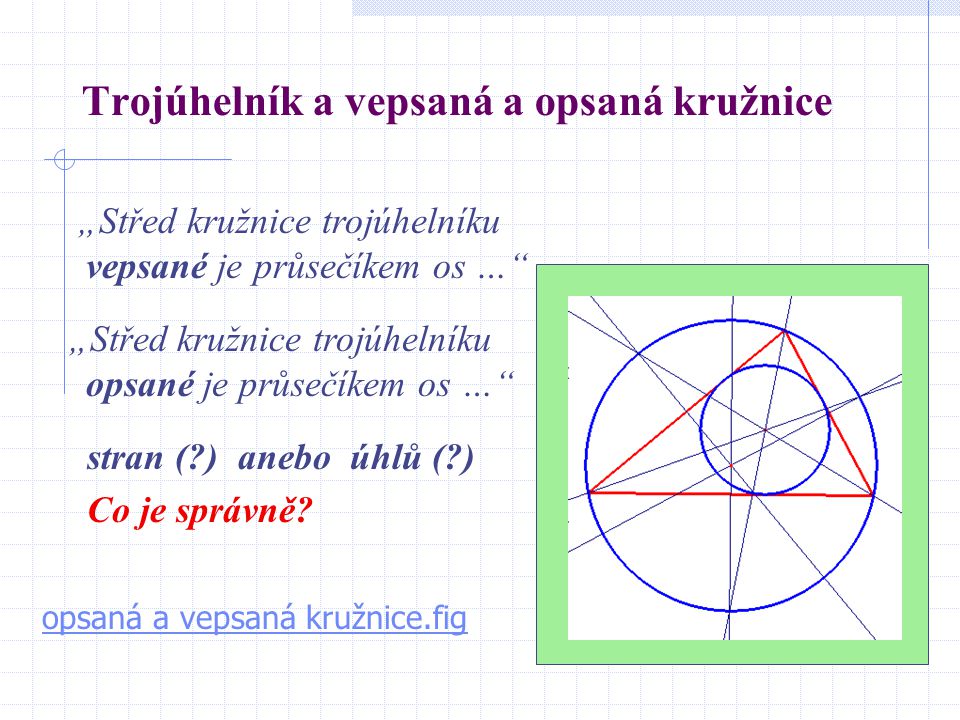
Kde leží střed kružnice vepsané
Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku.Sestrojíme osu o1 úhlu α. Sestrojíme osu o2 úhlu β. Průsečík os o1 a o2 je střed S kružnice vepsané k. Tuto kružnici sestrojíme, její poloměr je dán vzdáleností středu S a libovolné strany (určíme jej po sestrojení kolmice ze středu S na libovolnou stranu). Vzdálenost bodů A [xA], B [xB] na číselné ose je rovna absolutní hodnotě rozdílu reálných čísel xA a xB . Vzdálenost |AB| dvou bodů A [xA ; yA ; zA ], B [xB ; yB ; zB] v prostoru je dán vzorcem: Vzdálenost dvou bodů A, B je rovna velikosti ( délce ) úsečky AB.
Jak poznat že body leží na přímce : Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Co je to Thaletova kružnice : Závěr: Množinou M vrcholů všech pravých úhlů v rovině, jejichž ramena procházejí dvěma danými různými body A, B, je kružnice s průměrem AB s výjimkou bodů A,B. Tuto množinu nazýváme Thaletovou kružnicí.
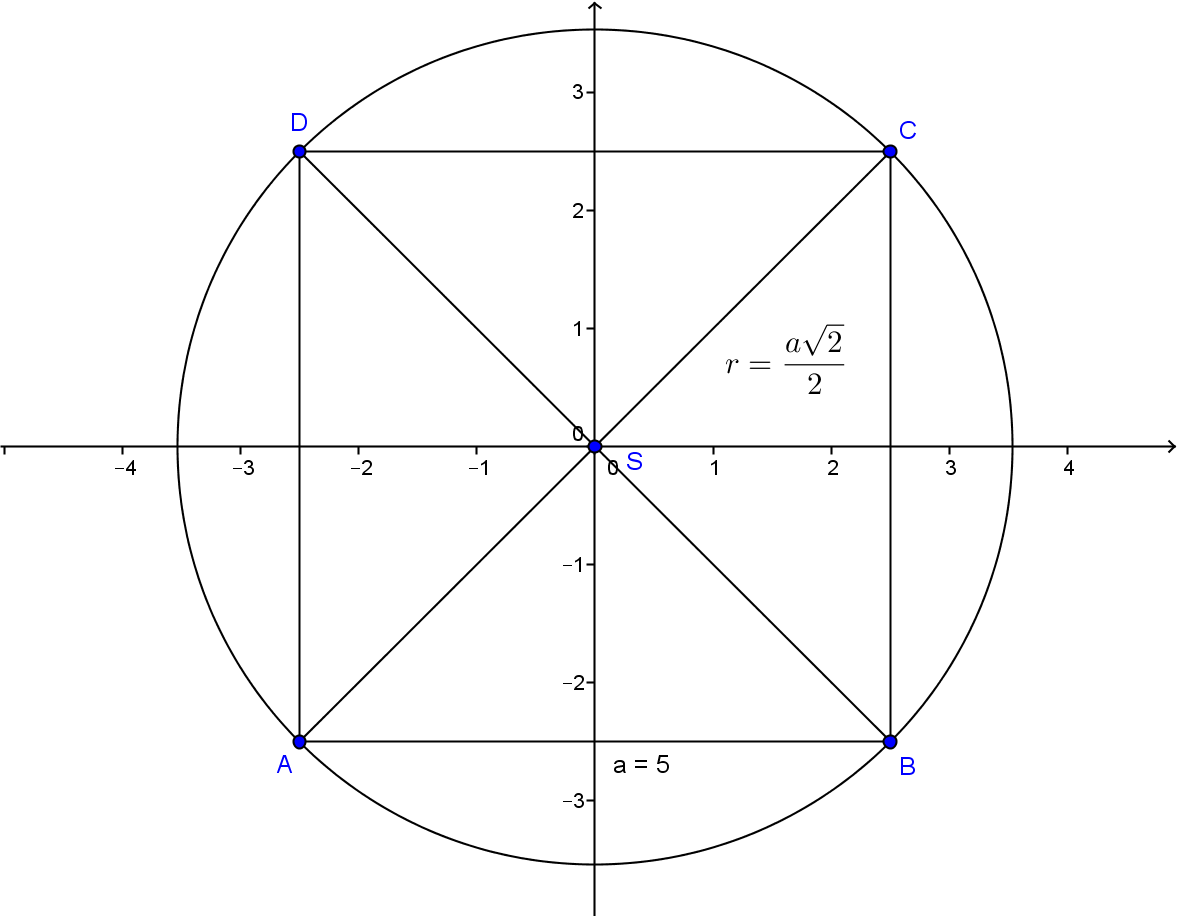
Jak vepsat do kružnice čtverec
Abyste sestrojili kružnici opsanou čtverci nebo obdélníku, nejprve za- kreslete úhlopříčky a pak narýsujte kružnici se středem v jejich průse- číku a procházející všemi čtyřmi vrcholy. Pro kružnici vepsanou čtverci narýsujte kružnici opět se středem v průsečíku úhlopříček a prochá- zející středy stran. Osa úhlu BAC je polopřímka, která rozděluje BAC na dva úhly stejné velikosti. Pro její body platí, že jejich vzdálenost od přímek (popř. stran) AB a AC je stejná.Kružnice opsaná
Taková kružnice má střed So, poloměr |SoA| a nazývá se opsaná, značíme ko.
Jak vypočítat délku oblouku kružnice : Délku a kruhového oblouku vypočítáme, když délku kružnice vydělíme číslem 360 a vynásobíme velikostí příslušného středového úhlu ve stupních.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak vypočítat střed kružnice opsané? Weitere Antworten – Jak najít střed kružnice opsané
Kružnice opsaná trojúhelníku. Střed kružnice opsané trojúhelníku je průsečík os stran trojúhelníku, poloměr se rovná vzdálenosti středu od libovolného vrcholu.Obvod kružnice se spočítá jako 3,14 [π] x průměr kružnice [d], nebo 2 x 3,14 [π] x poloměr kružnice [r].Poloměr kružnice opsané je vzdálenost středu od libovolného vrcholu. Střed kružnice vepsané leží na průsečíků os úhlů (je stejně daleko od všech stran trojúhelníku). Poloměr kružnice vepsané určíme pomocí kolmice na libovolnou stranu trojúhelníku procházející středem.
Jak se dělá kružnice vepsaná a opsaná : Kružnice opsaná prochází všemi třemi vrcholy trojúhelníku, kružnice vepsaná se dotýká všech tří stran trojúhelníka (strany jsou tečnami kružnice). Obě kružnice jsou třemi vrcholy trojúhelníka jednoznačně určené.
Jak zjistit zda bod leží na kružnici
1) Vzhledem k tomu, že známe souřadnice středu kružnice a poloměr, stačí sestavit středovou rovnici kružnice: k: (x-1)^2+(y-2)^2=4 (nulové body jsou x-ové a -yové souřadnice středu, 4 je poloměr^2. Poté stačí obrázek a je vidět, že K je vnitřním bodem a M leží na kružnici.
Jak na kružnicí vepsanou : Sestrojíme osu o1 úhlu α. Sestrojíme osu o2 úhlu β. Průsečík os o1 a o2 je střed S kružnice vepsané k. Tuto kružnici sestrojíme, její poloměr je dán vzdáleností středu S a libovolné strany (určíme jej po sestrojení kolmice ze středu S na libovolnou stranu).
Kružnice vepsaná
Taková kružnice má střed Sv, poloměr d(Sv, AB) a nazývá se vepsaná, značíme kv. Body dotyku vepsané kružnice s jednotlivými stranami značíme Ta, Tb, Tc.
Vzoreček pro výpočet obvodu kružnice je jednoduchý: Obvod kruhu o = 2 π (3,14) × poloměr r.
Kde leží střed kružnice vepsané
Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku.Sestrojíme osu o1 úhlu α. Sestrojíme osu o2 úhlu β. Průsečík os o1 a o2 je střed S kružnice vepsané k. Tuto kružnici sestrojíme, její poloměr je dán vzdáleností středu S a libovolné strany (určíme jej po sestrojení kolmice ze středu S na libovolnou stranu).
Vzdálenost bodů A [xA], B [xB] na číselné ose je rovna absolutní hodnotě rozdílu reálných čísel xA a xB . Vzdálenost |AB| dvou bodů A [xA ; yA ; zA ], B [xB ; yB ; zB] v prostoru je dán vzorcem: Vzdálenost dvou bodů A, B je rovna velikosti ( délce ) úsečky AB.
Jak poznat že body leží na přímce : Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.
Co je to Thaletova kružnice : Závěr: Množinou M vrcholů všech pravých úhlů v rovině, jejichž ramena procházejí dvěma danými různými body A, B, je kružnice s průměrem AB s výjimkou bodů A,B. Tuto množinu nazýváme Thaletovou kružnicí.
Jak vepsat do kružnice čtverec
Abyste sestrojili kružnici opsanou čtverci nebo obdélníku, nejprve za- kreslete úhlopříčky a pak narýsujte kružnici se středem v jejich průse- číku a procházející všemi čtyřmi vrcholy. Pro kružnici vepsanou čtverci narýsujte kružnici opět se středem v průsečíku úhlopříček a prochá- zející středy stran.
Osa úhlu BAC je polopřímka, která rozděluje BAC na dva úhly stejné velikosti. Pro její body platí, že jejich vzdálenost od přímek (popř. stran) AB a AC je stejná.Kružnice opsaná
Taková kružnice má střed So, poloměr |SoA| a nazývá se opsaná, značíme ko.
Jak vypočítat délku oblouku kružnice : Délku a kruhového oblouku vypočítáme, když délku kružnice vydělíme číslem 360 a vynásobíme velikostí příslušného středového úhlu ve stupních.