Obsah jedné stěny tj. jednoho čtverce vypočítáme jednoduše podle vzorce [S] = a × a. Výsledek následně vynásobíme šesti a tak získáme povrch krychle. Zjednodušení výpočtového vzorce: [S] = 6 × a × a => 6 × a2.Povrch tělesa je součet obsahů všech ploch, které těleso ohraničují.Odvozené vzorce
Strana z délky stranové úhlopříčky: a = u2 / √2.
Strana z délky tělesové úhlopříčky: a = u3 / √3.
Strana z plochy jedné strany krychle: a = √ P.
Strana z celkového povrchu krychle: a = √ (Q/6)
Strana z objemu krychle: a = 3√ V.
Jaký je vzoreček pro povrch kvádru : Kvádr má šest stěn a všechny jsou tvořené obdélníky, vždy dvě jsou stejně velké. Povrch kvádru vypočítáme jako: S = 2(ab + bc + ac).
Jak se počítá obsah pláště kvádru
Vzorce pro výpočet obsahu kvádru
Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Jaký je vzoreček pro objem krychle : U krychle jsou všechny tři rozměry stejné (délka, šířka a i výška), proto všem rozměrům u tohoto tělesa obecně přiřazujeme jedno písmenko – „a“. Objem krychle vypočítáme tak, že spočteme obsah podstavy (čtverec – S=a.a), kterou dále vynásobíme výškou krychle (a). Výsledná hodnota je v objemových jednotkách.
Obsah pláště je obsah stěny (trojúhelníku) vynásobený čtyřmi (stěny jsou čtyři). Obsah stěny (trojúhelníku) se vypočítá jako součin strany a k ní příslušné výšky (stěnová výška), dělený dvěma. Obsah povrchu těla můžeme přibližně vypočítat podle vzorce: S = 167∙√(hmotnost ∙ výška) m2.
Kolik má krychle stran
umime.to/FV6
mnohostěn
počet stěn
počet hran
krychle
6
12
osmistěn
8
12
dvanáctistěn
12
30
dvacetistěn
20
30
Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle.Boční stěny hranolu tvoří plášť hranolu. Výškou hranolu je vzdálenost obou podstav. OBJEM hranolu vypočítáme jako součin obsahu podstavy (SP) a výšky hranolu (v). V = SP · v POVRCH hranolu je roven součtu obsahů obou podstav (SP) hranolu a obsahu pláště hranolu SPL (SPL = S1 + S2 + S3 + S4). Vzorec pro výpočet objemu místnosti je tedy: V = a * b * c, kde a je délka, b je šířka a c je výška místnosti. Například, pokud má místnost délku 5 metrů, šířku 4 metry a výšku 3 metry, objem místnosti bude V = 5 * 4 * 3 = 60 metrů krychlových.
Jak se počítá obsah pláště válce : Obsah pláště: S p l = 2 π r ⋅ v S_{pl}=2\pi r \cdot v Spl=2πr⋅v. Povrch válce: S = 2 π r ⋅ ( r + v ) S=2\pi r \cdot (r + v) S=2πr⋅(r+v)
Jak Vypočitat obsah pláště : Obsah pláště se vypočítá jako součet obsahů všech jeho čtverců nebo obdélníků.
Jak vypočítat BSA
K výpočtu se používá rovnice dle DuBois: BSA = (hmotnost0.425 x výška0.725) x 0.007184. Základní vzorce pro výpočet povrchu, objemu
Základní jednotkou jsou metry čtverečné (m2). Objem nám pak říká, kolik například vody se do daného tělesa vejde, jedná se o vnitřek tělesa. Základní jednotkou jsou metry krychlové (m3). Velmi často se objem udává v litrech.
Krychle
Počet vrcholů
8
Počet hran
12
Počet stěn
6
Úhel u vrcholu
90°
Co pocitame u krychle : U krychle jsou všechny tři rozměry stejné (délka, šířka a i výška), proto všem rozměrům u tohoto tělesa obecně přiřazujeme jedno písmenko – „a“. Objem krychle vypočítáme tak, že spočteme obsah podstavy (čtverec – S=a.a), kterou dále vynásobíme výškou krychle (a). Výsledná hodnota je v objemových jednotkách.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak vypočítat plášť krychle? Weitere Antworten – Jaký je vzorec pro povrch krychle
Vzorce pro výpočet povrchu krychle
Obsah jedné stěny tj. jednoho čtverce vypočítáme jednoduše podle vzorce [S] = a × a. Výsledek následně vynásobíme šesti a tak získáme povrch krychle. Zjednodušení výpočtového vzorce: [S] = 6 × a × a => 6 × a2.Povrch tělesa je součet obsahů všech ploch, které těleso ohraničují.Odvozené vzorce
Jaký je vzoreček pro povrch kvádru : Kvádr má šest stěn a všechny jsou tvořené obdélníky, vždy dvě jsou stejně velké. Povrch kvádru vypočítáme jako: S = 2(ab + bc + ac).
Jak se počítá obsah pláště kvádru
Vzorce pro výpočet obsahu kvádru
Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].
Jaký je vzoreček pro objem krychle : U krychle jsou všechny tři rozměry stejné (délka, šířka a i výška), proto všem rozměrům u tohoto tělesa obecně přiřazujeme jedno písmenko – „a“. Objem krychle vypočítáme tak, že spočteme obsah podstavy (čtverec – S=a.a), kterou dále vynásobíme výškou krychle (a). Výsledná hodnota je v objemových jednotkách.
Obsah pláště je obsah stěny (trojúhelníku) vynásobený čtyřmi (stěny jsou čtyři). Obsah stěny (trojúhelníku) se vypočítá jako součin strany a k ní příslušné výšky (stěnová výška), dělený dvěma.
Obsah povrchu těla můžeme přibližně vypočítat podle vzorce: S = 167∙√(hmotnost ∙ výška) m2.
Kolik má krychle stran
umime.to/FV6
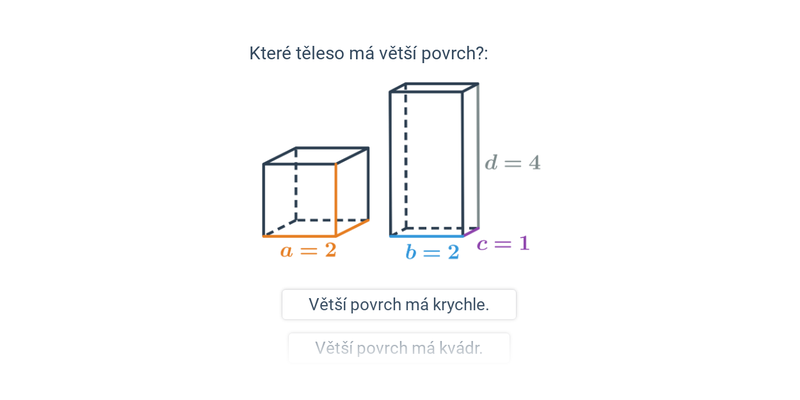
Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle.Boční stěny hranolu tvoří plášť hranolu. Výškou hranolu je vzdálenost obou podstav. OBJEM hranolu vypočítáme jako součin obsahu podstavy (SP) a výšky hranolu (v). V = SP · v POVRCH hranolu je roven součtu obsahů obou podstav (SP) hranolu a obsahu pláště hranolu SPL (SPL = S1 + S2 + S3 + S4).
Vzorec pro výpočet objemu místnosti je tedy: V = a * b * c, kde a je délka, b je šířka a c je výška místnosti. Například, pokud má místnost délku 5 metrů, šířku 4 metry a výšku 3 metry, objem místnosti bude V = 5 * 4 * 3 = 60 metrů krychlových.
Jak se počítá obsah pláště válce : Obsah pláště: S p l = 2 π r ⋅ v S_{pl}=2\pi r \cdot v Spl=2πr⋅v. Povrch válce: S = 2 π r ⋅ ( r + v ) S=2\pi r \cdot (r + v) S=2πr⋅(r+v)
Jak Vypočitat obsah pláště : Obsah pláště se vypočítá jako součet obsahů všech jeho čtverců nebo obdélníků.
Jak vypočítat BSA
K výpočtu se používá rovnice dle DuBois: BSA = (hmotnost0.425 x výška0.725) x 0.007184.
Základní vzorce pro výpočet povrchu, objemu
Základní jednotkou jsou metry čtverečné (m2). Objem nám pak říká, kolik například vody se do daného tělesa vejde, jedná se o vnitřek tělesa. Základní jednotkou jsou metry krychlové (m3). Velmi často se objem udává v litrech.
Co pocitame u krychle : U krychle jsou všechny tři rozměry stejné (délka, šířka a i výška), proto všem rozměrům u tohoto tělesa obecně přiřazujeme jedno písmenko – „a“. Objem krychle vypočítáme tak, že spočteme obsah podstavy (čtverec – S=a.a), kterou dále vynásobíme výškou krychle (a). Výsledná hodnota je v objemových jednotkách.