Antwort Jak vypadá čtyřstěn? Weitere Antworten – Co je to čtyřstěn

Jak vypadá čtyřstěn?
Čtyřstěn (zvaný též trojboký jehlan, tetraedr) je nejjednodušší mnohostěn, typ trojrozměrného tělesa. Je vymezen nejmenším možným počtem bodů, který může trojrozměrné těleso definovat, tzn. čtyřmi různými body v prostoru.umime.to/FV6

mnohostěn	počet stěn	počet hran
čtyřstěn	4	6
krychle	6	12
osmistěn	8	12
dvanáctistěn	12	30

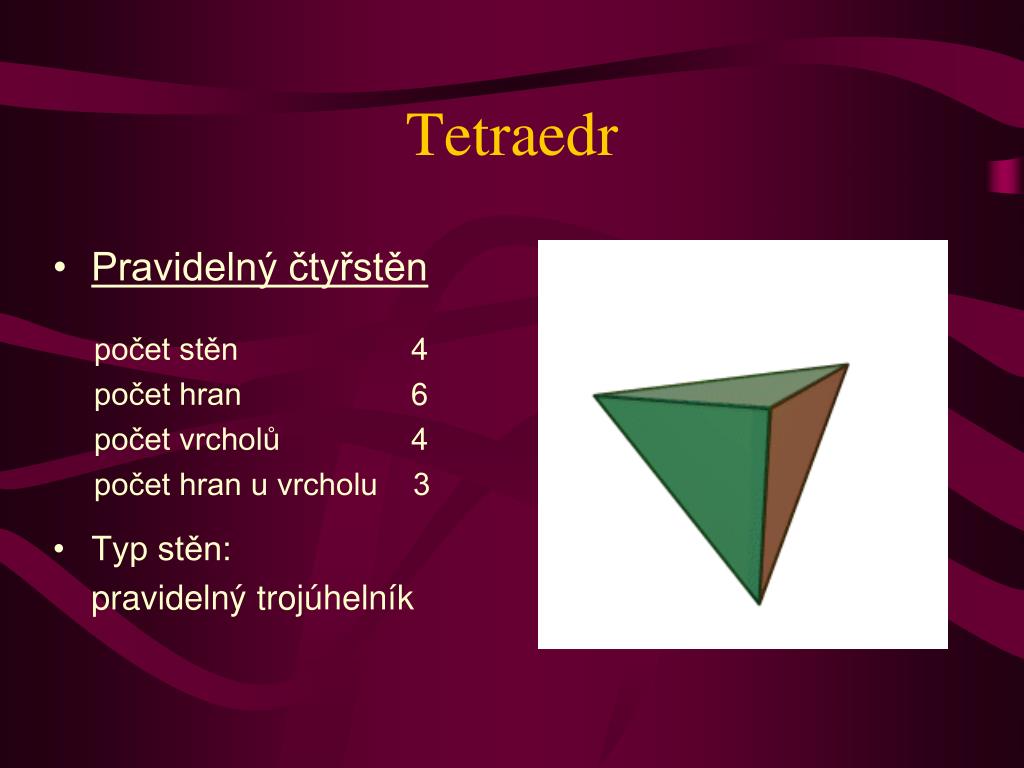
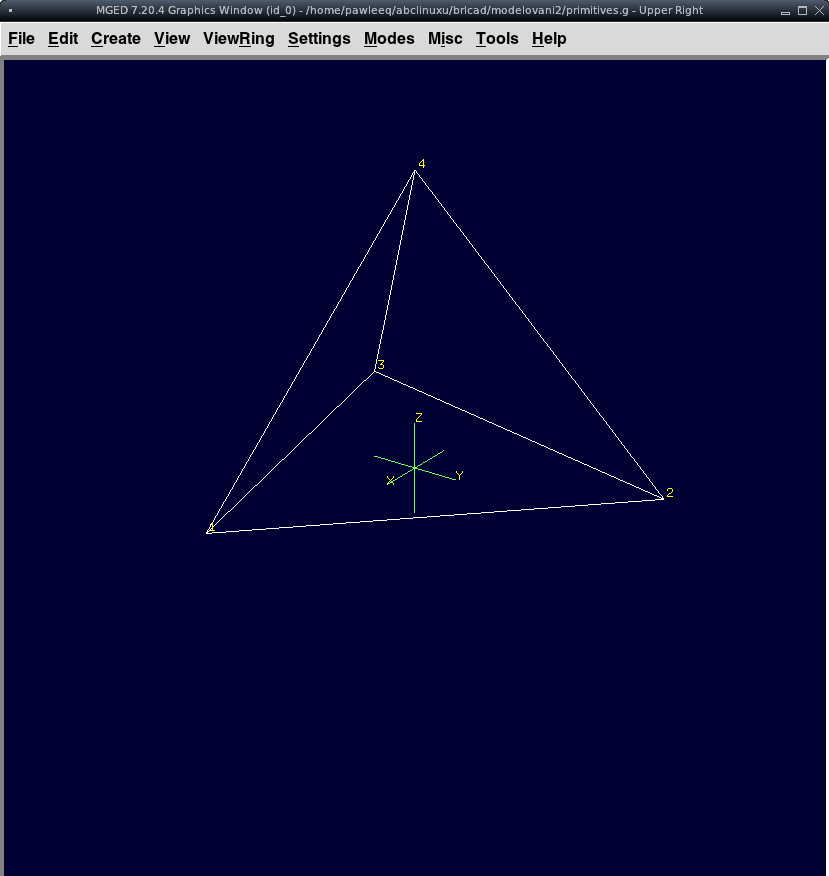
Trojboký jehlan, což je jehlan s nejmenším počtem stěn čtyři, nazýváme čtyřstěn (obr. 4.4.1). Jsou-li jeho stěny tvořeny čtyřmi navzájem shodnými rovnostrannými trojúhelníky, jedná se o pravidelný čtyřstěn (pravidelný tetraedr, viz obr. 4.4.2, který řadíme mezi Platónská tělesa).

Jak nazýváme pravidelná tělesa : Platónova tělesa jsou pravidelná tělesa.

Co je to mnohostěn

Mnohostěn, také polyedr je trojrozměrné geometrické těleso, jehož povrch se skládá z konečně mnoha stěn tvořených mnohoúhelníky. V moderním smyslu se pojem mnohostěn užívá nejen pro těleso trojrozměrné, ale obecně pro těleso n-rozměrné (speciálním případem n-rozměrného mnohostěnu je n-rozměrný simplex).

Kolik má koule stěn : Geometrická tělesa

Těleso	Koule
Popis	Koulíme s ní v ruce, po zemi, upozorňujeme dítě na to, že nemá žádné hrany, stěny, že vypadá pořad stejně. Oproti jiným tělesům ani chvíli nepostojí, pořád se hýbe.
Základna	žádná
Počet vrcholů	0
Počet hran	0

Pravidelný jehlan	trojboký	čtyřboký
Podstava	trojúhelník (rovnostranný)	čtverec (kosočtverec)
Počet vrcholů	4	5
Počet hran	6	8
Počet bočních stěn	3	4

Pravidelný čtyřstěn je jehlan, jehož základnu i všechny tři boční stěny jsou rovnostranné trojúhelníky. Tento čtyřstěn má stejný tvar všech stěn i délku všech hran – jedná se tedy o jedno z platónských těles.

Kolik hran má Dvanáctistěn

Pravidelný dvanáctistěn

Stěny pravidelného dvanáctistěnu jsou tvořeny dvanácti shodnými pravidelnými pětiúhelníky. Toto těleso má dvacet vrcholů a třicet hran, viz obr.Dodekaedr je pravidelný dvanáctistěn, jehož každou stěnu tvoří pravidelný pětiúhelník. Pravidelné mnohostěny mají tři společné vlastnosti – jedná se o konvexní těleso, z každého vrcholu vychází stejný počet hran, každá ze stěn je ohraničena stejným počtem hran (každá ze stěn je pravidelný n-úhelník).Platónova tělesa jsou pravidelná tělesa. Pravidelná znamená, že všechny stěny tvoří shodné pravidelné mnohoúhelníky a z každého vrcholu tělesa vychází stejný počet hran. Tato tělesa jsou známá už z doby 5.

Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.

Kolik má krychle stěn : Krychle má šest shodných stěn čtvercového tvaru, osm vrcholů a dvanáct hran stejné délky.

Jak se pocita Ctyrboky jehlan : Objem jehlanu se spočítá jako obsah podstavy [Sp] krát výška jehlanu [v] lomeno třemi. Přičemž obsah podstavy [Sp] vypočítáme vzorcem pro obsah čtverce, tedy a2.

Co je ve tvaru jehlanu

Tvar jehlanu mají egyptské pyramidy, stan, věže kostelů, hradů atd. = jehlan, jehož podstavou je čtverec a boční stěny jsou rovnoramenné trojúhelníky.

Vzorec pro výpočet objemu jehlanu

Objem jehlanu se spočítá jako obsah podstavy [Sp] krát výška jehlanu [v] lomeno třemi. Přičemž obsah podstavy [Sp] vypočítáme vzorcem pro obsah čtverce, tedy a2.