Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.Obecná rovnice. Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.⇒ Kritérium rovnoběžnosti přímky a roviny: Přímka p je rovnoběžná s rovinou ρ , jestliže v rovině ρ leží alespoň jedna přímka p′, která je s přímkou p rovnoběžná.
Kolik spolecnych bodů mohou mít 2 různoběžné přímky : Závěr: Různoběžné přímky mají společný právě jeden bod.
Kdy je přímka kolmá k rovině
Přímka a rovina jsou k sobě kolmé právě tehdy, když je přímka kolmá ke všem přímkám roviny.
Jak zjistit zda bod leží na přímce : Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC. AB = (1; -2; 2), AC = (-1; 2; -1).
Obecná rovnice přímky v rovině má tvar: a x + b y + c = 0 ax+by+c=0 ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.
Odchylka přímky a roviny
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.
Jak vypočítat vzdálenost dvou přímek
Vzdálenost dvou mimoběžných přímek je rovna minimální vzdálenosti kterýchkoliv dvou jejich bodů. Dvojice bodů, která určuje tuto vzdálenost, je právě jedna. Jsou to body X[x1; x2; x3] na přímce p a Y[y1; y2; y3] na přímce q takové, že přímka XY je kolmá jak na přímku p, tak na přímku q.Kruh a kružnice
U každého bodu v rovině pak můžeme určit, kde leží: na kružnici (jejich vzdálenost od S je rovna r) ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici) ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici)Kritérium kolmosti dvou rovin: Obsahuje-li rovina σ přímku p kolmou k rovině ρ, pak jsou roviny σ, ρ k sobě kolmé. Definice: Je-li přímka p kolmá k rovině ρ, pak její odchylka od ρ je 90°. Není-li p kolmá k ρ a je-li p1 pravoúhlý průmět p do ρ, nazýváme odchylkou přímky p od roviny ρ odchylku přímek p, p1.
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.
Jak urcit Polorovinu : Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Tato přímka se nazývá hraniční. Polorovinu s hraniční přímkou p procházející bodem K značíme ↦ p K \mapsto pK ↦pK. Je-li přímka p určena body A, B, můžeme také psát ↦ A B K \mapsto ABK ↦ABK.
Co když rovnice nemá řešení : Soustava nemá žádné řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne neplatná rovnost. Soustava má nekonečně mnoho řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne platná rovnost.
Jak se počítá odchylka přímek
Odchylka přímky a roviny
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2. Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q.
Odchylka rovin ρ a ψ, je rovna odchylce přímek p a q, pro které platí p = (ρ ∩ σ), q = (ψ ∩ σ), kde σ je rovina kolmá na ρ i ψ.Průměrná odchylka je součet absolutních hodnot rozdílu každého datového bodu a průměru datové sady, dělený počtem prvků v datové sadě.
Jak vypočítat vzdálenost dvou bodu : Vzdálenost bodů A [xA], B [xB] na číselné ose je rovna absolutní hodnotě rozdílu reálných čísel xA a xB . Vzdálenost |AB| dvou bodů A [xA ; yA ; zA ], B [xB ; yB ; zB] v prostoru je dán vzorcem: Vzdálenost dvou bodů A, B je rovna velikosti ( délce ) úsečky AB.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak určit vzájemnou polohu rovin? Weitere Antworten – Jak určit vzájemnou polohu přímek
Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.Obecná rovnice. Obecná rovnice přímky v rovině má tvar ax+by+c=0 , kde a,b,c jsou nějaká reálná čísla taková, že alespoň jedno z čísel a a b není rovno 0. Body ležící na této přímce jsou právě ty bodyX=(x,y), jejichž souřadnice splňují uvedenou rovnost.⇒ Kritérium rovnoběžnosti přímky a roviny: Přímka p je rovnoběžná s rovinou ρ , jestliže v rovině ρ leží alespoň jedna přímka p′, která je s přímkou p rovnoběžná.
Kolik spolecnych bodů mohou mít 2 různoběžné přímky : Závěr: Různoběžné přímky mají společný právě jeden bod.
Kdy je přímka kolmá k rovině
Přímka a rovina jsou k sobě kolmé právě tehdy, když je přímka kolmá ke všem přímkám roviny.
Jak zjistit zda bod leží na přímce : Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC. AB = (1; -2; 2), AC = (-1; 2; -1).
Obecná rovnice přímky v rovině má tvar: a x + b y + c = 0 ax+by+c=0 ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.
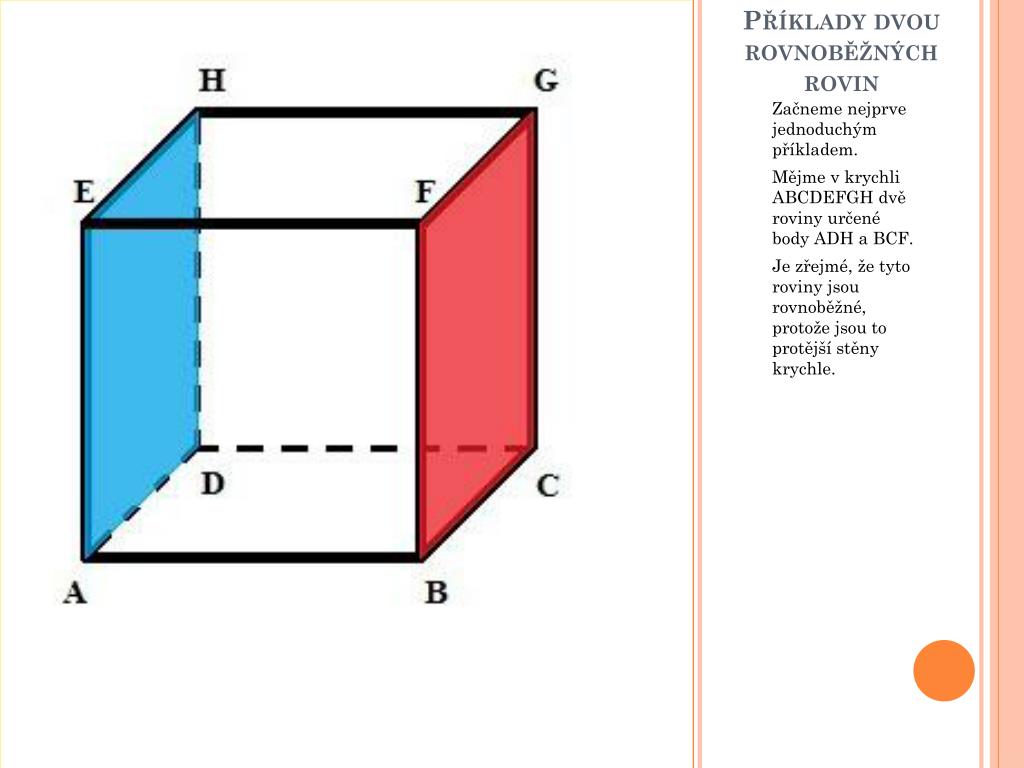
Odchylka přímky a roviny
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.
Jak vypočítat vzdálenost dvou přímek
Vzdálenost dvou mimoběžných přímek je rovna minimální vzdálenosti kterýchkoliv dvou jejich bodů. Dvojice bodů, která určuje tuto vzdálenost, je právě jedna. Jsou to body X[x1; x2; x3] na přímce p a Y[y1; y2; y3] na přímce q takové, že přímka XY je kolmá jak na přímku p, tak na přímku q.Kruh a kružnice
U každého bodu v rovině pak můžeme určit, kde leží: na kružnici (jejich vzdálenost od S je rovna r) ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici) ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici)Kritérium kolmosti dvou rovin: Obsahuje-li rovina σ přímku p kolmou k rovině ρ, pak jsou roviny σ, ρ k sobě kolmé. Definice: Je-li přímka p kolmá k rovině ρ, pak její odchylka od ρ je 90°. Není-li p kolmá k ρ a je-li p1 pravoúhlý průmět p do ρ, nazýváme odchylkou přímky p od roviny ρ odchylku přímek p, p1.
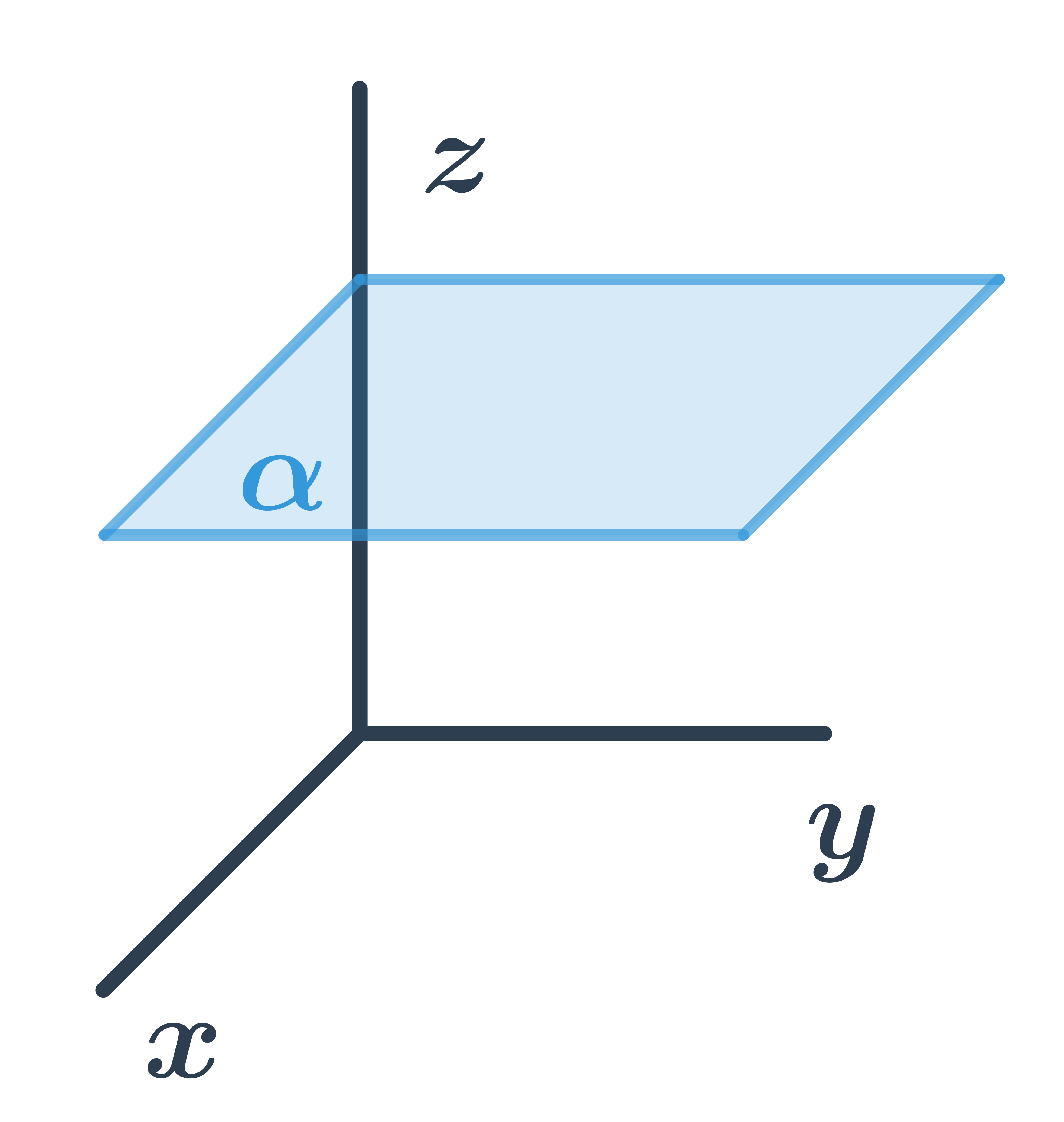
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je: φ = π/2 – α.
Jak urcit Polorovinu : Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Tato přímka se nazývá hraniční. Polorovinu s hraniční přímkou p procházející bodem K značíme ↦ p K \mapsto pK ↦pK. Je-li přímka p určena body A, B, můžeme také psát ↦ A B K \mapsto ABK ↦ABK.
Co když rovnice nemá řešení : Soustava nemá žádné řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne neplatná rovnost. Soustava má nekonečně mnoho řešení – po dosazení se ve vzniklé rovnici odečte i druhá neznámá a vznikne platná rovnost.
Jak se počítá odchylka přímek
Odchylka přímky a roviny
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2. Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ. Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q.
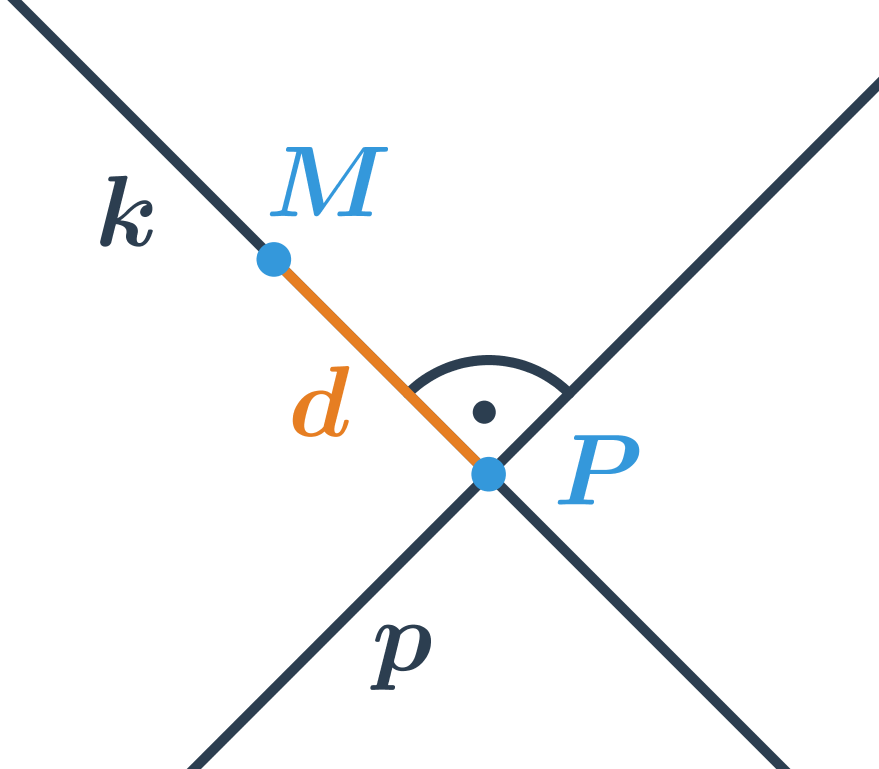
Odchylka rovin ρ a ψ, je rovna odchylce přímek p a q, pro které platí p = (ρ ∩ σ), q = (ψ ∩ σ), kde σ je rovina kolmá na ρ i ψ.Průměrná odchylka je součet absolutních hodnot rozdílu každého datového bodu a průměru datové sady, dělený počtem prvků v datové sadě.
Jak vypočítat vzdálenost dvou bodu : Vzdálenost bodů A [xA], B [xB] na číselné ose je rovna absolutní hodnotě rozdílu reálných čísel xA a xB . Vzdálenost |AB| dvou bodů A [xA ; yA ; zA ], B [xB ; yB ; zB] v prostoru je dán vzorcem: Vzdálenost dvou bodů A, B je rovna velikosti ( délce ) úsečky AB.