➢ Věta USU: Trojúhelník lze sestrojit podle věty USU, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. ➢ Věta Ssu: Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich.8. Jak sestrojit trojúhelník, známe-li všechny tři strany
Sestrojíme úsečku AB o délce 7 cm.
Z bodu A sestrojíme oblouk kružnice s poloměrem 5 cm.
Z bodu B sestrojíme oblouk kružnice s poloměrem 6 cm → vznikne bod C.
Sestrojením úseček AC a BC dokončíme konstrukci trojúhelníku ABC.
Při řešení jednodušších úloh sestrojujeme trojúhelníky, pro které známe délky stran. Nesmíme přitom zapomínat, že platí tzv. trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
Jak označit trojúhelník : Trojúhelník je geometrický útvar, který má tři vrcholy, tři strany a tři úhly. Vrcholy se označují velkými tiskacími písmeny, případně velkými tiskacími písmeny s indexem vpravo dole. (např. A, B, C, D, A1, A2, …)
Co znamená věta usu
Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné. Věta Ssu: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu naproti větší z nich, jsou shodné.
Který trojúhelník nelze sestrojit : Dneska si ukážeme, jak poznat ze zadání délek stran trojúhelníku, že trojúhelník nejde narýsovat. Takovému postupu říkáme TROJÚHELNÍKOVÁ NEROVNOST – V každém trojúhelníku platí, že součet délek libovolných dvou jeho stran je větší než délka strany třetí.
Výšky se rýsuje celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice protla právě bod C. To je vše. Červeně jsou vyznačeny všechny tři výšky trojúhelníku. Všimněte si, že každá výška je kolmá ke své straně. TROJÚHELNÍK je mnohoúhelník, jednoznačně určený třemi různými body, jež neleží v jedné přímce. V každém trojúhelníku je součet délek libovolných dvou stran větší než délka strany třetí. Této vlastnosti říkáme TROJÚHELNÍKOVÁ NEROVNOST.
Jak vypada obecny trojúhelník
Trojúhelník je rovinný obrazec tvořený třemi vrcholy a třemi úsečkami. Obecný trojúhelník označujeme vrcholy A, B a C. přičemž jednotlivé úsečky můžeme zapsat jejich krajními body nebo jako strany, jejichž název má stejné, jen malé, písmeno jako protější vrchol.TROJÚHELNÍK je mnohoúhelník, jednoznačně určený třemi různými body, jež neleží v jedné přímce. V každém trojúhelníku je součet délek libovolných dvou stran větší než délka strany třetí. Této vlastnosti říkáme TROJÚHELNÍKOVÁ NEROVNOST.Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. VĚTA sus Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.
Co je to věta SSS : Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.
Jak se pocita Trojuhelnikova nerovnost : Trojúhelníková nerovnost je matematická věta: V každém trojúhelníku platí, že součet délek kterýchkoliv dvou stran je vždy větší než délka strany třetí.
Jak zjistím vysku v trojúhelníku
Výška v trojúhelníku je vlastně vzdálenost vrcholu od protější strany. Vzdálenost se měří vždy na kolmici, proto je to kolmice spuštěná z vrcholu na protější stranu. Výška trojúhelníku je kolmá úsečka spuštěná z vrcholu na přímku procházející protější stranou. Průsečík výšky s touto přímkou se nazývá pata výšky. Každý trojúhelník má tři výšky.V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Jak udělat výšky v trojúhelníku : Výšky se rýsují celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice procházela právě bodem C. Výšku můžeme vést z každého vrcholu trojúhelníka. Všechny výšky se pak protínají v bodě, které se nazývá průsečík výšek.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak správně sestrojit trojúhelník? Weitere Antworten – Jak sestrojit trojúhelník podle věty usu
➢ Věta USU: Trojúhelník lze sestrojit podle věty USU, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. ➢ Věta Ssu: Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich.8. Jak sestrojit trojúhelník, známe-li všechny tři strany
Při řešení jednodušších úloh sestrojujeme trojúhelníky, pro které známe délky stran. Nesmíme přitom zapomínat, že platí tzv. trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
Jak označit trojúhelník : Trojúhelník je geometrický útvar, který má tři vrcholy, tři strany a tři úhly. Vrcholy se označují velkými tiskacími písmeny, případně velkými tiskacími písmeny s indexem vpravo dole. (např. A, B, C, D, A1, A2, …)
Co znamená věta usu
Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné. Věta Ssu: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu naproti větší z nich, jsou shodné.
Který trojúhelník nelze sestrojit : Dneska si ukážeme, jak poznat ze zadání délek stran trojúhelníku, že trojúhelník nejde narýsovat. Takovému postupu říkáme TROJÚHELNÍKOVÁ NEROVNOST – V každém trojúhelníku platí, že součet délek libovolných dvou jeho stran je větší než délka strany třetí.
Výšky se rýsuje celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice protla právě bod C. To je vše. Červeně jsou vyznačeny všechny tři výšky trojúhelníku. Všimněte si, že každá výška je kolmá ke své straně.
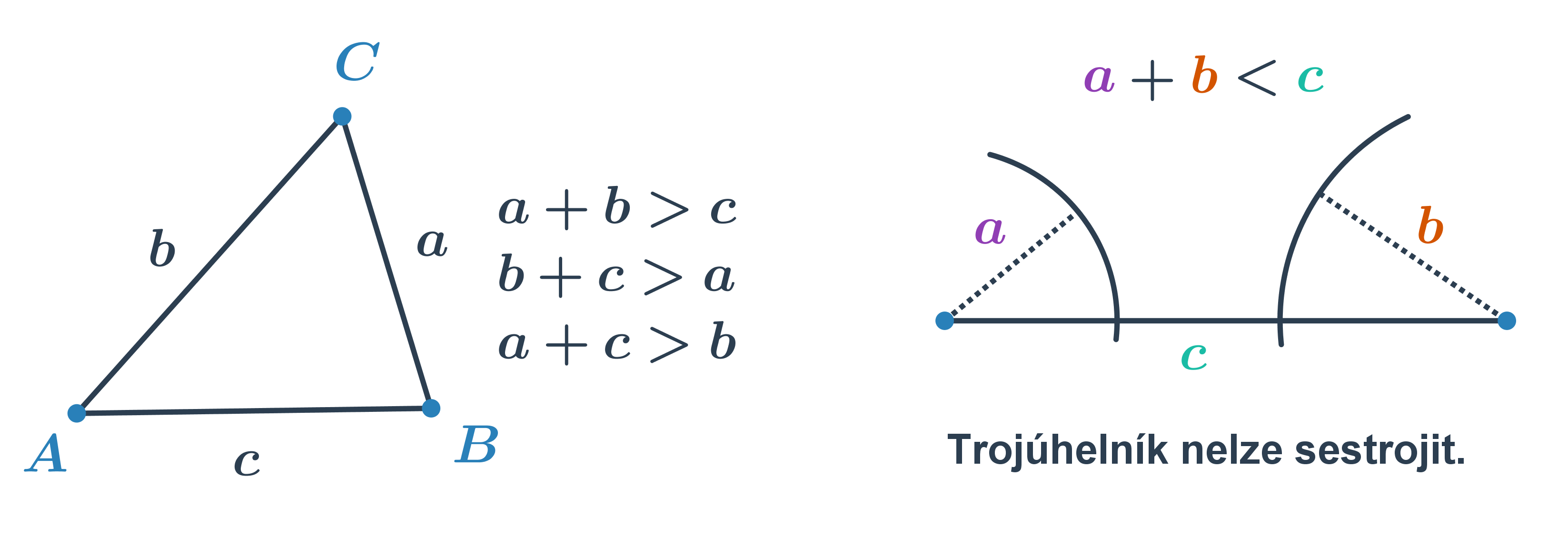
TROJÚHELNÍK je mnohoúhelník, jednoznačně určený třemi různými body, jež neleží v jedné přímce. V každém trojúhelníku je součet délek libovolných dvou stran větší než délka strany třetí. Této vlastnosti říkáme TROJÚHELNÍKOVÁ NEROVNOST.
Jak vypada obecny trojúhelník
Trojúhelník je rovinný obrazec tvořený třemi vrcholy a třemi úsečkami. Obecný trojúhelník označujeme vrcholy A, B a C. přičemž jednotlivé úsečky můžeme zapsat jejich krajními body nebo jako strany, jejichž název má stejné, jen malé, písmeno jako protější vrchol.TROJÚHELNÍK je mnohoúhelník, jednoznačně určený třemi různými body, jež neleží v jedné přímce. V každém trojúhelníku je součet délek libovolných dvou stran větší než délka strany třetí. Této vlastnosti říkáme TROJÚHELNÍKOVÁ NEROVNOST.Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné.
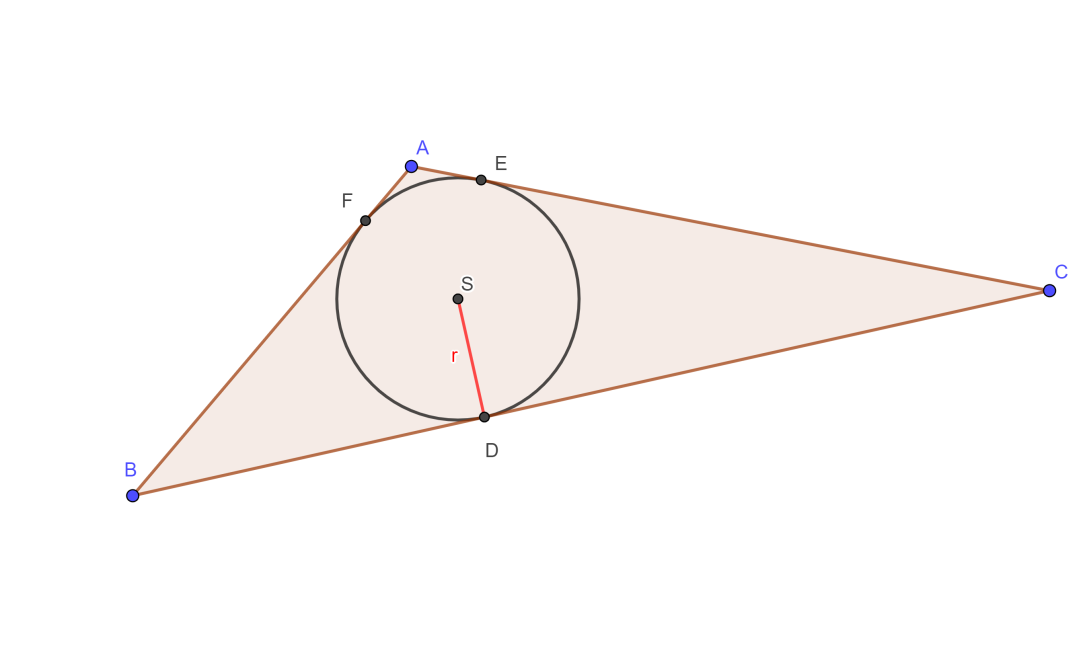
VĚTA sus Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.
Co je to věta SSS : Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.
Jak se pocita Trojuhelnikova nerovnost : Trojúhelníková nerovnost je matematická věta: V každém trojúhelníku platí, že součet délek kterýchkoliv dvou stran je vždy větší než délka strany třetí.
Jak zjistím vysku v trojúhelníku
Výška v trojúhelníku je vlastně vzdálenost vrcholu od protější strany. Vzdálenost se měří vždy na kolmici, proto je to kolmice spuštěná z vrcholu na protější stranu.
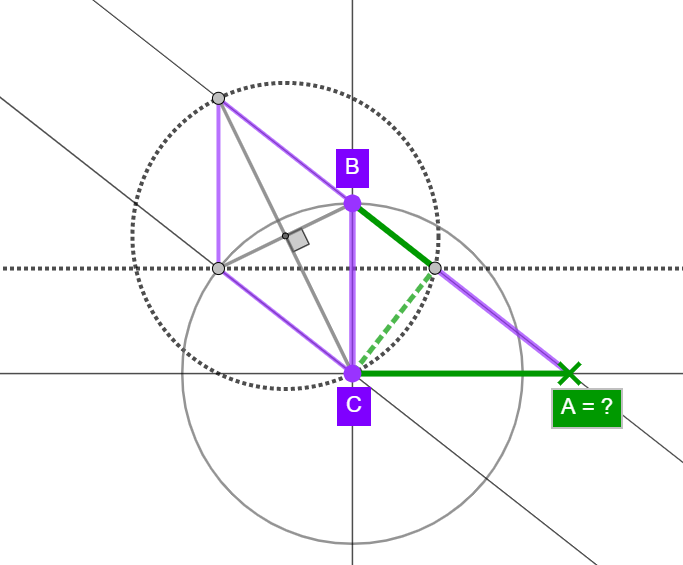
Výška trojúhelníku je kolmá úsečka spuštěná z vrcholu na přímku procházející protější stranou. Průsečík výšky s touto přímkou se nazývá pata výšky. Každý trojúhelník má tři výšky.V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Jak udělat výšky v trojúhelníku : Výšky se rýsují celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice procházela právě bodem C. Výšku můžeme vést z každého vrcholu trojúhelníka. Všechny výšky se pak protínají v bodě, které se nazývá průsečík výšek.