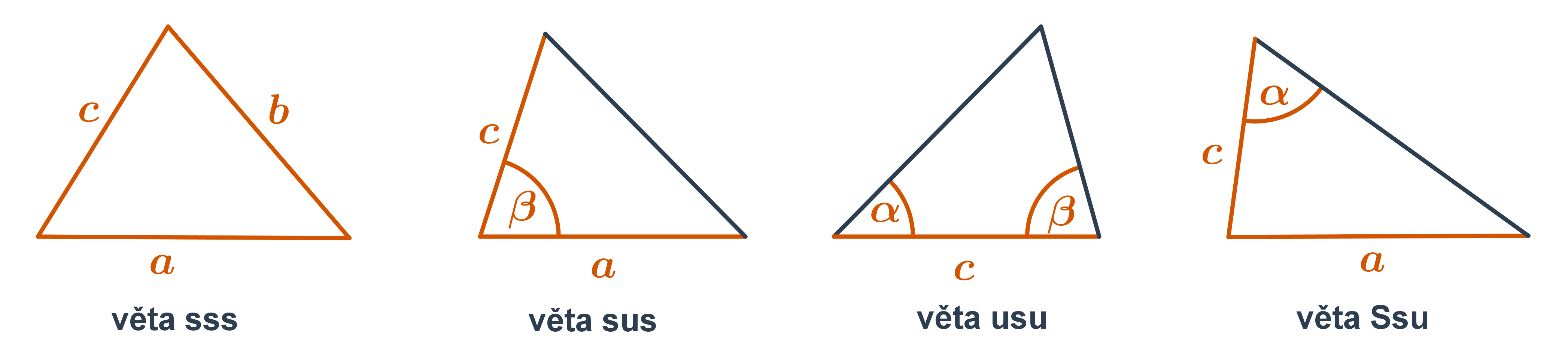
Věta usu Trojúhelník lze sestrojit podle věty usu, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. Věta Ssu Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich. Velikost zadaného úhlu je menší než 180°.Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné. Věta Ssu: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu naproti větší z nich, jsou shodné.VĚTA sss Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících si stran, jsou podobné. VĚTA sus Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.
Jak se počítá podobnost : Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení. Je-li poměr podobnosti k ˂ 1, jedná se o zmenšení.
Kdy lze sestrojit trojúhelník
trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
Jak sestrojit SSS : Věty o sestrojitelnosti trojúhelníků: ➢ Věta SSS: Trojúhelník lze sestrojit podle věty SSS, jsou-li dány 3 jeho strany, pro které platí trojúhelníková nerovnost. ➢ Věta SUS: Trojúhelník lze sestrojit podle věty SUS, jsou-li dány 2 jeho strany a úhel jimi sevřený. Velikost zadaného úhlu je menší než 180°.
Věta Ssu: Shodují-li se dva trojúhelníky ve dvou stranách a úhlu proti větší z nich, jsou shodné. Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm.
Jak se zapisuje podobnost
Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm.Poměr vzdálenosti dvou bodů daného geometrického útvaru a vzdálenosti odpovídajících dvou bodů jiného geometrického útvaru (referenčního) je u podobných útvarů shodný pro každou takovou dvojici bodů a nazývá se koeficient podobnosti. Podobnost zachovává velikost úhlů a poměr délek.8. Jak sestrojit trojúhelník, známe-li všechny tři strany
Sestrojíme úsečku AB o délce 7 cm.
Z bodu A sestrojíme oblouk kružnice s poloměrem 5 cm.
Z bodu B sestrojíme oblouk kružnice s poloměrem 6 cm → vznikne bod C.
Sestrojením úseček AC a BC dokončíme konstrukci trojúhelníku ABC.
Věta USU: Pokud se dva trojúhelníky shodují v jedné straně a v obou úhlech k této straně přilehlých, pak jsou shodné.
Který trojúhelník nelze sestrojit : Dneska si ukážeme, jak poznat ze zadání délek stran trojúhelníku, že trojúhelník nejde narýsovat. Takovému postupu říkáme TROJÚHELNÍKOVÁ NEROVNOST – V každém trojúhelníku platí, že součet délek libovolných dvou jeho stran je větší než délka strany třetí.
Co je to podobnost : podobnost (obecný pojem) – vlastnost různých věcí nebo dějů, kdy se liší (jen) některé charakteristiky nebo vlastnosti těchto věcí či se jejich charakteristiky liší jen málo.
Jak udělat pravý úhel bez Úhloměru
Pokud potřebujete přeměřit, zda stěny místnosti svírají pravé úhly, stačí použít posuvný metr o dostatečné délce a změřit obě úhlopříčky z protějších rohů místnosti. V případě, že je půdorys místnosti přesným čtvercem nebo obdélníkem, budou délky obou úhlopříček stejné. Věta usu: Shodují-li se dva trojúhelníky ve straně a v obou přilehlých úhlech, jsou shodné.8. Jak sestrojit trojúhelník, známe-li všechny tři strany
Sestrojíme úsečku AB o délce 7 cm.
Z bodu A sestrojíme oblouk kružnice s poloměrem 5 cm.
Z bodu B sestrojíme oblouk kružnice s poloměrem 6 cm → vznikne bod C.
Sestrojením úseček AC a BC dokončíme konstrukci trojúhelníku ABC.
Co je podobne zobrazeni : Definice: Zobrazení v rovině se nazývá podobným zobrazením (podobností), jestliže každé úsečce AB přiřazuje úsečku A´B´ pro jejíž velikost platí . Koeficient k nazýváme poměr podobnosti.
Antwort Jak sestrojit SSU? Weitere Antworten – Jak sestrojit trojúhelník SSU
Věta usu Trojúhelník lze sestrojit podle věty usu, je-li dána 1 jeho strana a 2 úhly k ní přiléhající. Součet velikosti daných úhlů je menší než 180°. Věta Ssu Trojúhelník lze sestrojit podle věty Ssu, jsou-li dány 2 jeho strany a úhel ležící proti delší z nich. Velikost zadaného úhlu je menší než 180°.Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné. Věta Ssu: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu naproti větší z nich, jsou shodné.VĚTA sss Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících si stran, jsou podobné. VĚTA sus Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.
Jak se počítá podobnost : Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení. Je-li poměr podobnosti k ˂ 1, jedná se o zmenšení.
Kdy lze sestrojit trojúhelník
trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
Jak sestrojit SSS : Věty o sestrojitelnosti trojúhelníků: ➢ Věta SSS: Trojúhelník lze sestrojit podle věty SSS, jsou-li dány 3 jeho strany, pro které platí trojúhelníková nerovnost. ➢ Věta SUS: Trojúhelník lze sestrojit podle věty SUS, jsou-li dány 2 jeho strany a úhel jimi sevřený. Velikost zadaného úhlu je menší než 180°.
Věta Ssu: Shodují-li se dva trojúhelníky ve dvou stranách a úhlu proti větší z nich, jsou shodné.
Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm.
Jak se zapisuje podobnost
Jestliže jsou poměry všech sobě odpovídajících stran trojúhelníků shodné, pak jsou tyto trojúhelníky podobné. Konstanta k je poměr podobnosti. ΔABC ~ ΔA´B´C´ Čteme: trojúhelník ABC je podobný trojúhelníku A´B´C´. Příklad: Je dán ΔABC: a = 28,2cm; b = 25,3 cm; c = 48,4 cm.Poměr vzdálenosti dvou bodů daného geometrického útvaru a vzdálenosti odpovídajících dvou bodů jiného geometrického útvaru (referenčního) je u podobných útvarů shodný pro každou takovou dvojici bodů a nazývá se koeficient podobnosti. Podobnost zachovává velikost úhlů a poměr délek.8. Jak sestrojit trojúhelník, známe-li všechny tři strany
Věta USU: Pokud se dva trojúhelníky shodují v jedné straně a v obou úhlech k této straně přilehlých, pak jsou shodné.
Který trojúhelník nelze sestrojit : Dneska si ukážeme, jak poznat ze zadání délek stran trojúhelníku, že trojúhelník nejde narýsovat. Takovému postupu říkáme TROJÚHELNÍKOVÁ NEROVNOST – V každém trojúhelníku platí, že součet délek libovolných dvou jeho stran je větší než délka strany třetí.
Co je to podobnost : podobnost (obecný pojem) – vlastnost různých věcí nebo dějů, kdy se liší (jen) některé charakteristiky nebo vlastnosti těchto věcí či se jejich charakteristiky liší jen málo.
Jak udělat pravý úhel bez Úhloměru
Pokud potřebujete přeměřit, zda stěny místnosti svírají pravé úhly, stačí použít posuvný metr o dostatečné délce a změřit obě úhlopříčky z protějších rohů místnosti. V případě, že je půdorys místnosti přesným čtvercem nebo obdélníkem, budou délky obou úhlopříček stejné.
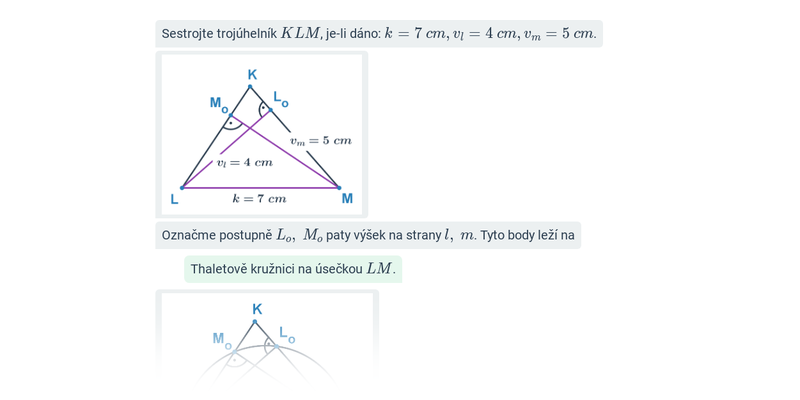
Věta usu: Shodují-li se dva trojúhelníky ve straně a v obou přilehlých úhlech, jsou shodné.8. Jak sestrojit trojúhelník, známe-li všechny tři strany
Co je podobne zobrazeni : Definice: Zobrazení v rovině se nazývá podobným zobrazením (podobností), jestliže každé úsečce AB přiřazuje úsečku A´B´ pro jejíž velikost platí . Koeficient k nazýváme poměr podobnosti.