Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Jak se počítá přepona v pravoúhlém trojúhelníku : Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Jak se vypočítá trojúhelník
Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.
Co platí v pravoúhlém trojúhelníku : V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách. V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Jak se vypočítává obsah trojúhelníku
Každý trojúhelník je v podstatě polovina plochy odpovídajícího obdélníku. Rozměry obdélníku jsou dány stranou trojúhelníka a odpovídající výškou rojúhleníku (viz. obrázek). Trojúhelník je polovinou obsahu obdélníka, proto obsah trojúhelníka je jedna polovina x strana x výška (straně odpovídající):Pravoúhlý trojúhelník má jeden vnitřní úhel o velikosti 90 stupňů. Oba zbývající vnitřní úhly musí mít nutně velikost menší než 90 stupňů, aby součet vnitřních úhlů byl roven 180 stupňů. Součet dvou zbývajících úhlů je tedy právě 90 stupňů.Pravoúhlý trojúhelník je takový trojúhelník, jehož jeden vnitřní úhel je pravý, tzn. má velikost 90°; jinými slovy, dvě ze stran pravoúhlého trojúhelníka jsou na sebe kolmé. Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2. Vybereme si stranu, kterou použijeme jako základnu a najdeme výšku na tuto základnu. Jejich délky pak dosadíme do vzorce pro výpočet obsahu.
Jak vypočítat cos : Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
Jak vypočítat třetí stranu pravoúhlého trojúhelníku : Pythagorova věta
c2 = a2 + b2 – tedy:
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených nad jeho odvěsnami.
Jak zjistit Preponu trojúhelníku
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu. Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak se počítá obvod trojúhelníku : Obvod u trojúhelníků a čtyřúhelníků je prostě součet délek jejich stran.
Antwort Jak se vypočítá pravoúhlého trojúhelníku? Weitere Antworten – Jak spočítat pravoúhlém trojúhelníku
Jak zjistit (bez rýsování), jestli je trojúhelník pravoúhlý Jestliže v trojúhelníku platí, že součet druhých mocnin délek dvou kratších stran je roven druhé mocnině délky nejdelší strany, potom je tento trojúhelník pravoúhlý.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
Jak se počítá přepona v pravoúhlém trojúhelníku : Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Jak se vypočítá trojúhelník
Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.
Co platí v pravoúhlém trojúhelníku : V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.

V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Jak se vypočítává obsah trojúhelníku
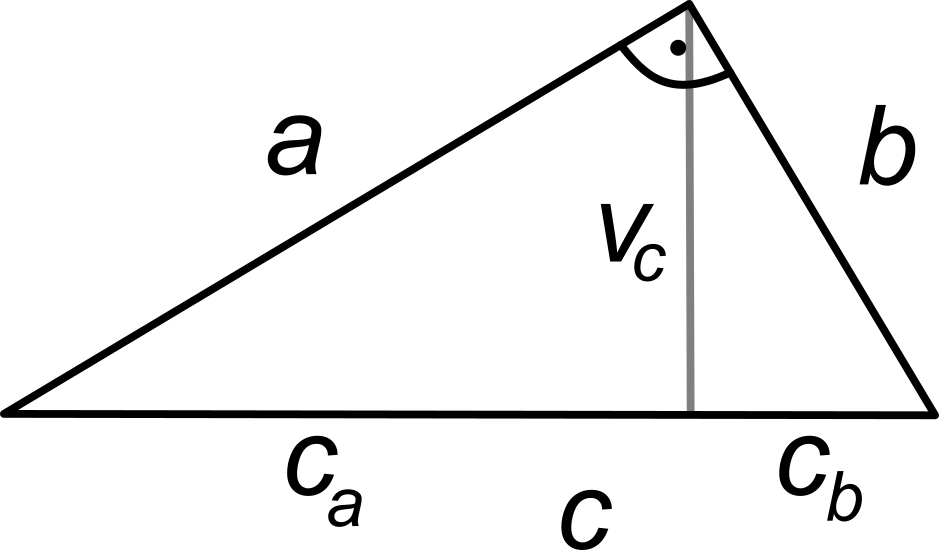
Každý trojúhelník je v podstatě polovina plochy odpovídajícího obdélníku. Rozměry obdélníku jsou dány stranou trojúhelníka a odpovídající výškou rojúhleníku (viz. obrázek). Trojúhelník je polovinou obsahu obdélníka, proto obsah trojúhelníka je jedna polovina x strana x výška (straně odpovídající):Pravoúhlý trojúhelník má jeden vnitřní úhel o velikosti 90 stupňů. Oba zbývající vnitřní úhly musí mít nutně velikost menší než 90 stupňů, aby součet vnitřních úhlů byl roven 180 stupňů. Součet dvou zbývajících úhlů je tedy právě 90 stupňů.Pravoúhlý trojúhelník je takový trojúhelník, jehož jeden vnitřní úhel je pravý, tzn. má velikost 90°; jinými slovy, dvě ze stran pravoúhlého trojúhelníka jsou na sebe kolmé.
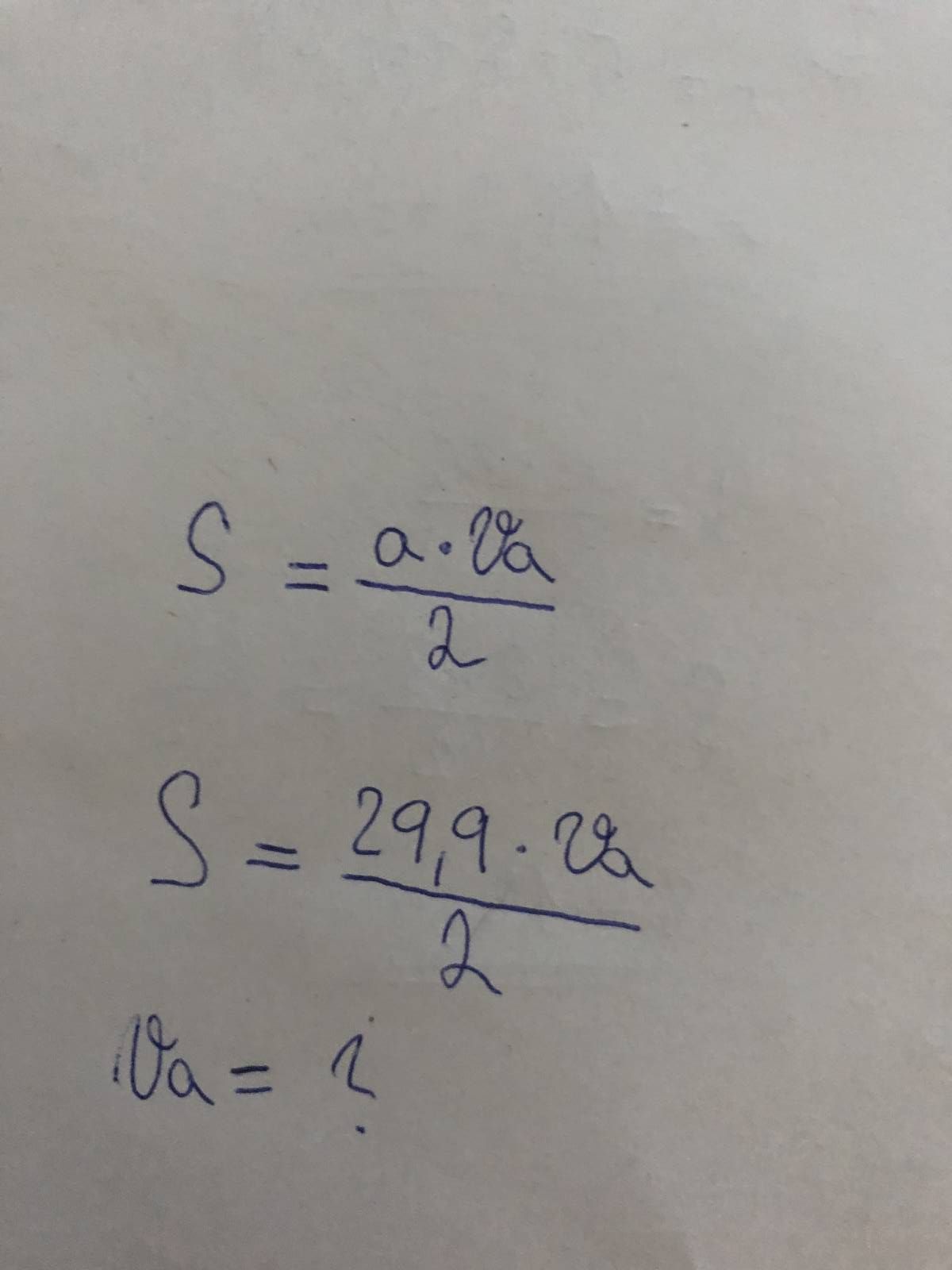
Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2. Vybereme si stranu, kterou použijeme jako základnu a najdeme výšku na tuto základnu. Jejich délky pak dosadíme do vzorce pro výpočet obsahu.
Jak vypočítat cos : Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
Jak vypočítat třetí stranu pravoúhlého trojúhelníku : Pythagorova věta
Jak zjistit Preponu trojúhelníku
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.
Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak se počítá obvod trojúhelníku : Obvod u trojúhelníků a čtyřúhelníků je prostě součet délek jejich stran.