Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Pythagorova věta
c2 = a2 + b2 – tedy:
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených nad jeho odvěsnami.
Jak zjistit Preponu trojúhelníku : Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.
Jak vypočítat 3 stranu trojúhelníku
Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Co rekl Pythagoras : Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Vypocitejte jeho vysku. Jak se pocita to cviceni To je pythagorova věta – c^2=a^2+b^2, kde c je rameno, a je výška a b polovina základny (výška v rovnoramenném trojúhelníku půlí základnu). Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak se značí Odvěsna
Co je vlastně ten pravoúhlý trojúhelník Pravoúhlý trojúhelník je geometrický útvar, jehož 2 strany svírají pravý úhel (= úhel o velikosti 90°). Těmto stranám se říká odvěsny a obecně se značí písmeny a, b.Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.Obsah trojúhelníku vypočítáme tak, že vynásobíme délku libovolné strany s výškou trojúhelníku, která je na tuto stranu kolmá, a to celé vydělíme dvěma. Pokud neznáte žádnou výšku, ale znáte délky všech stran trojúhelníku, můžete jeho obsah spočítat z Heronova vzorce. Metapontum Village, ItáliePythagoras / Úmrtí
Jak dlouho žil Pythagoras : Πυθαγόρας ο Σάμιος, okolo 570 př. n. l. ostrov Samos – po 510 př. n. l. Krotón v jižní Itálii) byl řecký filozof, matematik, astronom i kněz.
Jak se měří výška trojúhelníku : Výška v trojúhelníku je vlastně vzdálenost vrcholu od protější strany. Vzdálenost se měří vždy na kolmici, proto je to kolmice spuštěná z vrcholu na protější stranu.
Jak se počítá výška trojúhelníka
Výška trojúhelníku je kolmá úsečka spuštěná z vrcholu na přímku procházející protější stranou. Průsečík výšky s touto přímkou se nazývá pata výšky. Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška. Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Jak poznat síň cos TG : Goniometrické funkce a pravoúhlý trojúhelník
Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
Tangens ( tan) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky odvěsny přilehlé úhlu α.
Antwort Jak se počítá Pythagorova? Weitere Antworten – Jak se pocita Pythagora
Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Pythagorova věta
Jak zjistit Preponu trojúhelníku : Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna. Jsou takto nazvány vzhledem k danému úhlu.
Jak vypočítat 3 stranu trojúhelníku
Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Co rekl Pythagoras : Pythagorás ze Samu
První Řek, který si uvědomil, že Večerka i Jitřenka jsou jedna a tatáž planeta – Venuše. Prohlásil, že Země je kulatá a rozšířil Anaximandrův model sfér. V matematice proslul Pythagorovou větou pro pravoúhlý trojúhelník (kvadrát velikosti přepony je roven součtu kvadrátů velikostí odvěsen).
Vypocitejte jeho vysku. Jak se pocita to cviceni To je pythagorova věta – c^2=a^2+b^2, kde c je rameno, a je výška a b polovina základny (výška v rovnoramenném trojúhelníku půlí základnu).

Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak se značí Odvěsna
Co je vlastně ten pravoúhlý trojúhelník Pravoúhlý trojúhelník je geometrický útvar, jehož 2 strany svírají pravý úhel (= úhel o velikosti 90°). Těmto stranám se říká odvěsny a obecně se značí písmeny a, b.Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.Obsah trojúhelníku vypočítáme tak, že vynásobíme délku libovolné strany s výškou trojúhelníku, která je na tuto stranu kolmá, a to celé vydělíme dvěma. Pokud neznáte žádnou výšku, ale znáte délky všech stran trojúhelníku, můžete jeho obsah spočítat z Heronova vzorce.

Metapontum Village, ItáliePythagoras / Úmrtí
Jak dlouho žil Pythagoras : Πυθαγόρας ο Σάμιος, okolo 570 př. n. l. ostrov Samos – po 510 př. n. l. Krotón v jižní Itálii) byl řecký filozof, matematik, astronom i kněz.
Jak se měří výška trojúhelníku : Výška v trojúhelníku je vlastně vzdálenost vrcholu od protější strany. Vzdálenost se měří vždy na kolmici, proto je to kolmice spuštěná z vrcholu na protější stranu.
Jak se počítá výška trojúhelníka
Výška trojúhelníku je kolmá úsečka spuštěná z vrcholu na přímku procházející protější stranou. Průsečík výšky s touto přímkou se nazývá pata výšky. Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška.
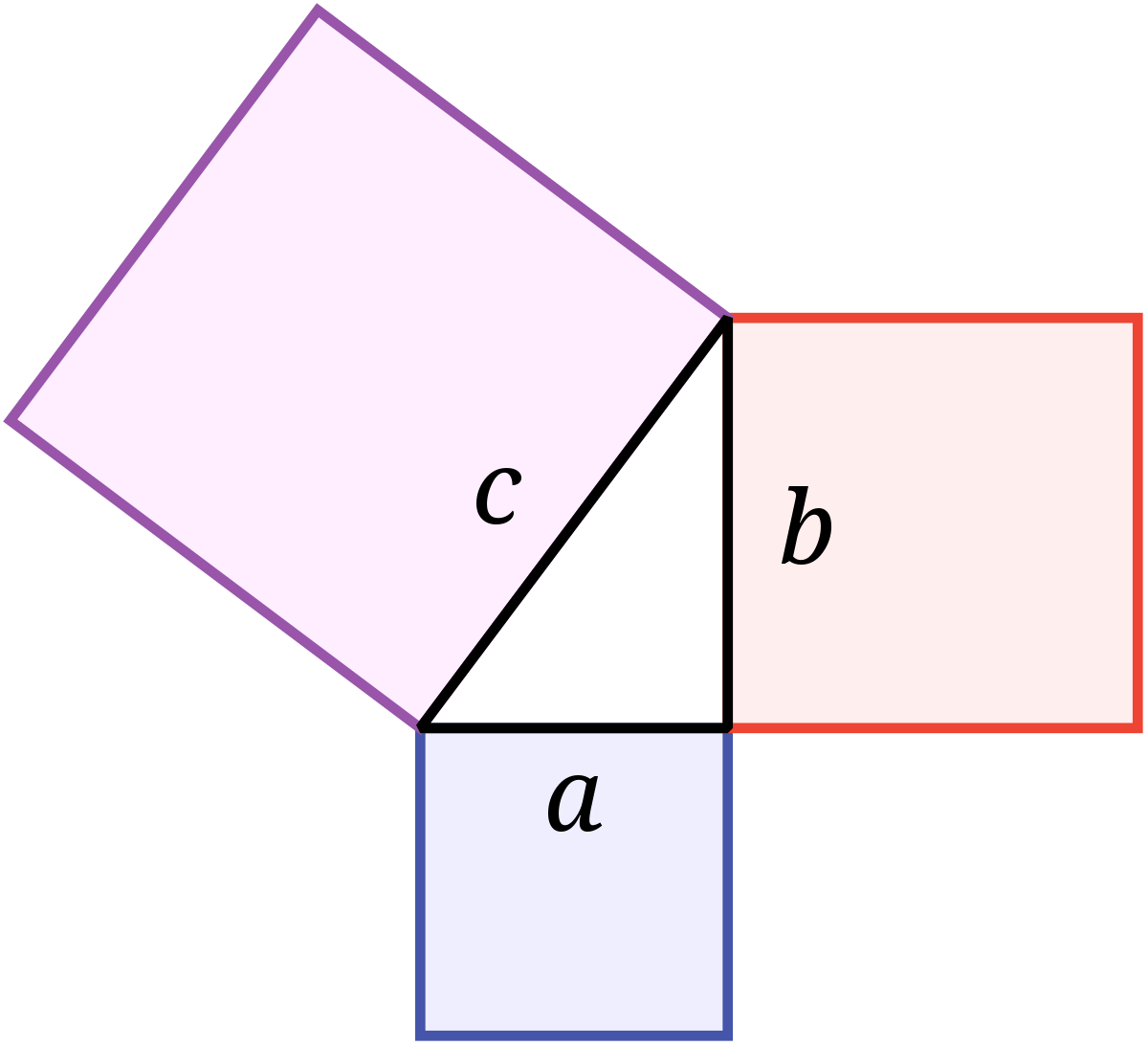
Pythagorovu větu můžeme zapsat vztahem c² = a² + b², kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Jak poznat síň cos TG : Goniometrické funkce a pravoúhlý trojúhelník