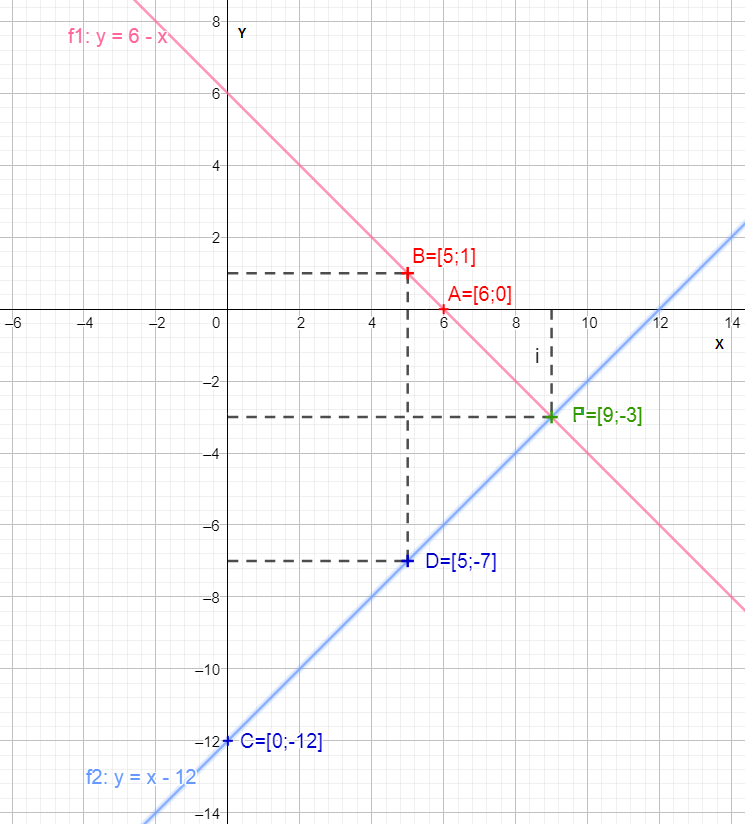
Vzorové řešení soustavy dvou lineárních rovnic se dvěma neznámými:
Vhodným vynásobením rovnic odstraníme zlomky.
Převedeme neznámé na jednu a konstanty na druhou stranu.
Aplikujeme sčítací metodu.
Vyřešíme lineární rovnici pro y.
Dosadíme y do rovnice před použitím sčítací metody.
Vyřešíme lineární rovnici pro x.
Řešíme-li lineární rovnici ax + b = 0, kde a, b ∈ R , nastane právě jedna z možností: a) a = 0 , rovnice má jedno řešení x = − b a ; b) a = 0, b = 0 , řešením rovnice jsou všechna x ∈ R ; c) a = 0, b = 0 , rovnice nemá řešení.Pokud rovnice obsahuje zlomek, ve kterém se vyskytuje neznámá ve jmenovateli, musíme rovnici nejdříve vynásobit jmenovatelem (případně společným násobkem všech jmenovatelů). Tím rovnici převedeme na základní rovnici, kterou řešíme běžným postupem.
Jak se dělá sčítací metoda : Sčítací metoda
Při řešení sčítací metodou sečteme (či odečteme) odděleně levé a pravé strany obou rovnic. Tato úprava vede k cíli, pokud nám při této operaci jedna z proměnných vypadne. V některých případech je proto nutné nejdříve jednu z rovnic vynásobit vhodným číslem.
Kdy se učí rovnice na základní škole
Soustavy rovnic je jedno z témat, které se běžně probírá na základních školách v osmém, či devátém ročníku.
Jak se počítá rovnice o jedné neznámé : Řešení rovnice se nezmění, jestliže odečteme od obou stran rovnice stejný výraz. Řešení rovnice se nezmění, jestliže vynásobíme obě strany rovnice stejným číslem nebo výrazem různým od nuly.
Pro řešení rovnice v součinovém tvaru využijeme pravidlo, že součin dvou a více činitelů je roven nule právě tehdy, když alespoň jeden z činitelů je nula. Každý činitel položíme roven nule. 0x je protokol, který umožňuje výměnu aktiv založených na platformě Ethereum peer-to-peer (P2P). Protokol vyvinutý společností 0x Labs slouží jako otevřený standard a základní stavební prvek DeFi pro všechny vývojáře, kteří vyžadují možnosti výměny.
Jak se počítá rovnice o 3 neznámých
Soustava tří lineárních rovnic o třech neznámých má jedno, žádné nebo nekonečně mnoho řešení. Z libovolné rovnice vyjádříme jednu neznámou. Získaný výraz dosadíme za tuto neznámou do zbývajících dvou rovnic. Dvě nově vzniklé rovnice o dvou neznámých tvoří soustavu.Nejjednodušší rovnice obsahují pouze lineární výrazy, tj. vyskytují se v nich pouze konstanty a násobky proměnné x. Rovnici upravujeme pomocí ekvivaletních úprav: přičítání a odčítání stejného výrazu k oběma stranám rovnice, úpravy výrazů na levé a pravé straně.Tato metoda řešení funguje tak, že z jedné rovnice vyjádří neznámou a toto vyjádření dosadí do druhé rovnice. Tak dostaneme jednu rovnici o jedné neznámé, kterou vyřešíme a dopočítáme i druhou neznámou. Jako příklad použije výše zmíněnou soustavu. 5. třída (5. ročník) – Rovnice – Procvičování online – Umíme matiku.
V jaké třídě se učí procenta : Matematika: 9. třída (9. ročník)
Téma
Aritmetika: Logaritmus
Zlomky, procenta, desetinná čísla: Zlomky
1 / 38
Zlomky, procenta, desetinná čísla: Procenta
0 / 17
Zlomky, procenta, desetinná čísla: Desetinná čísla
0 / 23
Jak se počítá neznámá : Neznámé mají stejné vlastnosti jako jejich hledané hodnoty a lze s nimi nejčastěji zacházet jako s čísly: lze je sčítat, odčítat a násobit, jen při dělení neznámou je třeba zajistit, že její hodnotou nebude nula.
Co kdyz vyjde rovnice 0 0
0 0 = – platná rovnost ⇒3 je řešením rovnice, Z nabízených čísel jsou řešením rovnice čísla 1 a 3. Pro převod čísel z desítkové soustavy se používá algoritmus využívající zbytků po celočíselném dělení základem požadované soustavy (pro dvojkovou soustavu je to číslo 2 , pro šestnáctkovou 16 atd.). Převáděné číslo vydělíme základem požadované soustavy, zapíšeme si zbytek do řetězce a výsledek dělení si uložíme.Soustavu vyřešíme dosazovací metodou (můžeme si vybrat také sčítací nebo srovnávací metodu). výraz dosadíme za neznámou z do druhé rovnice. Získanou rovnici s neznámou y vyřešíme. Hodnotu neznámé y dosadíme do vyjádření neznámé z a vypočítáme její hodnotu.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak se pocita rovnice o dvou neznámých? Weitere Antworten – Jak Vypocitat rovnici o dvou neznámých
Vzorové řešení soustavy dvou lineárních rovnic se dvěma neznámými:
Řešíme-li lineární rovnici ax + b = 0, kde a, b ∈ R , nastane právě jedna z možností: a) a = 0 , rovnice má jedno řešení x = − b a ; b) a = 0, b = 0 , řešením rovnice jsou všechna x ∈ R ; c) a = 0, b = 0 , rovnice nemá řešení.Pokud rovnice obsahuje zlomek, ve kterém se vyskytuje neznámá ve jmenovateli, musíme rovnici nejdříve vynásobit jmenovatelem (případně společným násobkem všech jmenovatelů). Tím rovnici převedeme na základní rovnici, kterou řešíme běžným postupem.
Jak se dělá sčítací metoda : Sčítací metoda
Při řešení sčítací metodou sečteme (či odečteme) odděleně levé a pravé strany obou rovnic. Tato úprava vede k cíli, pokud nám při této operaci jedna z proměnných vypadne. V některých případech je proto nutné nejdříve jednu z rovnic vynásobit vhodným číslem.
Kdy se učí rovnice na základní škole
Soustavy rovnic je jedno z témat, které se běžně probírá na základních školách v osmém, či devátém ročníku.
Jak se počítá rovnice o jedné neznámé : Řešení rovnice se nezmění, jestliže odečteme od obou stran rovnice stejný výraz. Řešení rovnice se nezmění, jestliže vynásobíme obě strany rovnice stejným číslem nebo výrazem různým od nuly.
Pro řešení rovnice v součinovém tvaru využijeme pravidlo, že součin dvou a více činitelů je roven nule právě tehdy, když alespoň jeden z činitelů je nula. Každý činitel položíme roven nule.
0x je protokol, který umožňuje výměnu aktiv založených na platformě Ethereum peer-to-peer (P2P). Protokol vyvinutý společností 0x Labs slouží jako otevřený standard a základní stavební prvek DeFi pro všechny vývojáře, kteří vyžadují možnosti výměny.
Jak se počítá rovnice o 3 neznámých
Soustava tří lineárních rovnic o třech neznámých má jedno, žádné nebo nekonečně mnoho řešení. Z libovolné rovnice vyjádříme jednu neznámou. Získaný výraz dosadíme za tuto neznámou do zbývajících dvou rovnic. Dvě nově vzniklé rovnice o dvou neznámých tvoří soustavu.Nejjednodušší rovnice obsahují pouze lineární výrazy, tj. vyskytují se v nich pouze konstanty a násobky proměnné x. Rovnici upravujeme pomocí ekvivaletních úprav: přičítání a odčítání stejného výrazu k oběma stranám rovnice, úpravy výrazů na levé a pravé straně.Tato metoda řešení funguje tak, že z jedné rovnice vyjádří neznámou a toto vyjádření dosadí do druhé rovnice. Tak dostaneme jednu rovnici o jedné neznámé, kterou vyřešíme a dopočítáme i druhou neznámou. Jako příklad použije výše zmíněnou soustavu.
5. třída (5. ročník) – Rovnice – Procvičování online – Umíme matiku.
V jaké třídě se učí procenta : Matematika: 9. třída (9. ročník)
Jak se počítá neznámá : Neznámé mají stejné vlastnosti jako jejich hledané hodnoty a lze s nimi nejčastěji zacházet jako s čísly: lze je sčítat, odčítat a násobit, jen při dělení neznámou je třeba zajistit, že její hodnotou nebude nula.
Co kdyz vyjde rovnice 0 0
0 0 = – platná rovnost ⇒3 je řešením rovnice, Z nabízených čísel jsou řešením rovnice čísla 1 a 3.
Pro převod čísel z desítkové soustavy se používá algoritmus využívající zbytků po celočíselném dělení základem požadované soustavy (pro dvojkovou soustavu je to číslo 2 , pro šestnáctkovou 16 atd.). Převáděné číslo vydělíme základem požadované soustavy, zapíšeme si zbytek do řetězce a výsledek dělení si uložíme.Soustavu vyřešíme dosazovací metodou (můžeme si vybrat také sčítací nebo srovnávací metodu). výraz dosadíme za neznámou z do druhé rovnice. Získanou rovnici s neznámou y vyřešíme. Hodnotu neznámé y dosadíme do vyjádření neznámé z a vypočítáme její hodnotu.
Jaké jsou druhy rovnic :