Pro výpočet objemu komolého jehlanu s obsahy podstav S1, S2 a výšce v použijeme vzorec V=31(S1+ S1S2+S2)v .
Pravidelný jehlan
trojboký
čtyřboký
Podstava
trojúhelník (rovnostranný)
čtverec (kosočtverec)
Počet vrcholů
4
5
Počet hran
6
8
Počet bočních stěn
3
4
Jehlan je prostorový geometrický útvar, který má jednu podstavu a plášť tvořený trojúhelníky. Podstava jehlanu může být libovolný mnohoúhelník (například čtverec, obdélník nebo trojúhelník) a všechny boční stěny (plášť) se setkávají v jednom společném bodě nazývaném vrchol jehlanu.
Kolik má trojboký jehlan : Trojboký jehlan, což je jehlan s nejmenším počtem stěn čtyři, nazýváme čtyřstěn (obr. 4.4.1). Jsou-li jeho stěny tvořeny čtyřmi navzájem shodnými rovnostrannými trojúhelníky, jedná se o pravidelný čtyřstěn (pravidelný tetraedr, viz obr.
Jak se pocita Ctyrboky jehlan
Objem jehlanu se spočítá jako obsah podstavy [Sp] krát výška jehlanu [v] lomeno třemi. Přičemž obsah podstavy [Sp] vypočítáme vzorcem pro obsah čtverce, tedy a2.
Jak se počítá objem : Vzorec pro výpočet objemu místnosti je tedy: V = a * b * c, kde a je délka, b je šířka a c je výška místnosti. Například, pokud má místnost délku 5 metrů, šířku 4 metry a výšku 3 metry, objem místnosti bude V = 5 * 4 * 3 = 60 metrů krychlových.
Stěny pravidelného čtyřstěnu jsou tvořeny čtyřmi shodnými rovnostrannými trojúhelníky. Toto těleso má čtyři vrcholy a šest hran, viz obr. Povrch jehlanu
je součet obsahů všech jeho stěn. Obsah postavy vypočítám dle toho, o jaký obrazec se jedná – čtverec, pětiúhelník, šestiúhelník, apod. Plášť se pak skládá z několika trojúhelníků – vypočítám tedy obsah jednoho trojúhelníku (stěny) a následně jej vynásobím počtem trojúhelníků – stěn (dle podstavy).
Jak se počítá spl
Boční stěny hranolu tvoří plášť hranolu. Výškou hranolu je vzdálenost obou podstav. OBJEM hranolu vypočítáme jako součin obsahu podstavy (SP) a výšky hranolu (v). V = SP · v POVRCH hranolu je roven součtu obsahů obou podstav (SP) hranolu a obsahu pláště hranolu SPL (SPL = S1 + S2 + S3 + S4).NEJHLEDANĚJŠÍ PŘEVODY VELIČINY OBJEM
1 litr = 10 decilitrů 1 mililitr = 1 x 10 -6 metrů krychlových.
Změříme si vnitřní rozměry a vypočítáme podle známého vzorce objemu kvádru V = a*b*c. Při naměřené délce 150 cm, šířce 45 cm a hloubce 30 cm počítáme 150*45*30 = 202 500 cm³ = 202 l = 0,2 kubíků. Pravidelný čtyřstěn je tvořen čtyřmi stejnými rovnostrannými trojúhelníky. Pravidelný čtyřstěn patří mezi takzvaná platónská tělesa. Pravidelný čtyřstěn je také trojrozměrným případem obecnějšího útvaru – simplexu. Spojením středů hran pravidelného čtyřstěnu vznikne pravidelný osmistěn vepsaný původnímu čtyřstěnu.
Kolik má kvádr hran : Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Jak Vypocitat povrch Pravidelneho Ctyrbokeho jehlanu : Povrch hranatých těles
Jehlan má jednu podstavu a plášť, povrch je tedy S = S p + S p l S=S_p+S_{pl} S=Sp+Spl. Stěny kvádru jsou obdélníky, přičemž vždy dvě jsou stejně velké. Povrch tedy vypočítáme jako S = 2 ( a b + a c + b c ) S = 2(ab+ac+bc) S=2(ab+ac+bc).
Jak Narysovat pravidelny Trojboky jehlan
Pravidelný trojboký hranol, jehlan
Podstavou je v obou případech rovnostranný trojúhelník. Výšku hranolu nanášíme v původní velikosti na boční hrany. Výšku jehlanu sestrojíme v těžišti trojúhelníku v původní velikosti. Povrch hranatých těles
Jehlan má jednu podstavu a plášť, povrch je tedy S = S p + S p l S=S_p+S_{pl} S=Sp+Spl. Stěny kvádru jsou obdélníky, přičemž vždy dvě jsou stejně velké. Povrch tedy vypočítáme jako S = 2 ( a b + a c + b c ) S = 2(ab+ac+bc) S=2(ab+ac+bc).Objem libovolného hranolu je součin obsahu podstavy a výšky: V = S p ⋅ v V=S_p\cdot v V=Sp⋅v. Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = a b c V = abc V=abc.
Kolik je čtvrt litru : Hájkova kronika uvádí jednotku věrtel jakožto jednotku užívanou pro kapaliny ve velikosti 1 věrtel = 248 litrů, což je 128 pint – což je tzv. pivní sud (jednotka). Ruská jednotka четверть (čtvrť) má přibližně 210 litrů.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak se pocita pravidelny Ctyrboky jehlan? Weitere Antworten – Jak vypočítat objem komolého jehlanu
Pro výpočet objemu komolého jehlanu s obsahy podstav S1, S2 a výšce v použijeme vzorec V=31(S1+ S1S2+S2)v .
Jehlan je prostorový geometrický útvar, který má jednu podstavu a plášť tvořený trojúhelníky. Podstava jehlanu může být libovolný mnohoúhelník (například čtverec, obdélník nebo trojúhelník) a všechny boční stěny (plášť) se setkávají v jednom společném bodě nazývaném vrchol jehlanu.
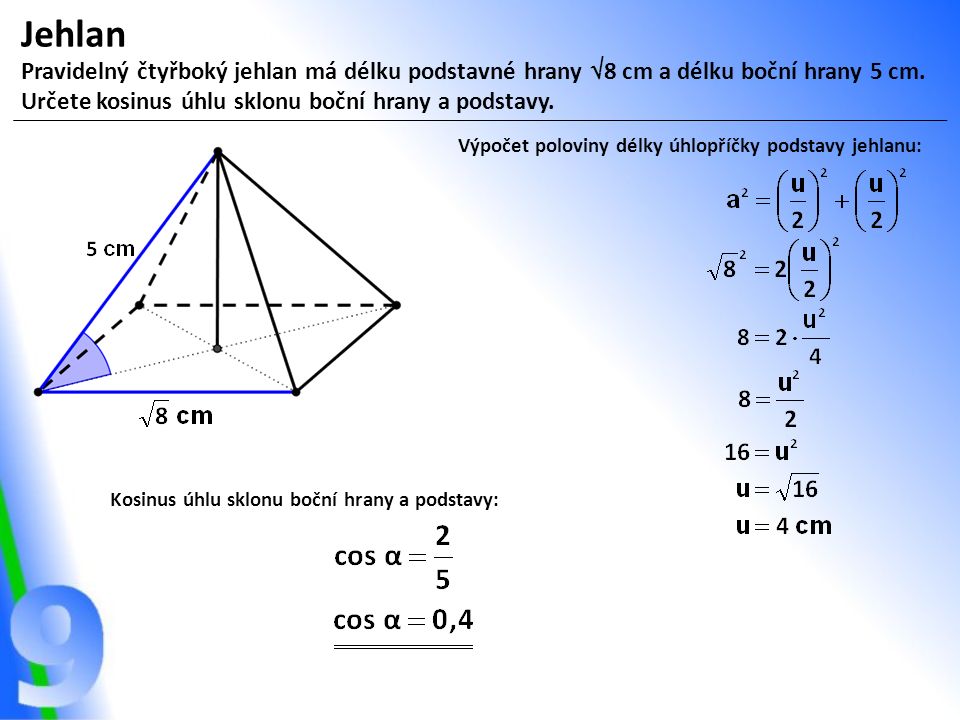
Kolik má trojboký jehlan : Trojboký jehlan, což je jehlan s nejmenším počtem stěn čtyři, nazýváme čtyřstěn (obr. 4.4.1). Jsou-li jeho stěny tvořeny čtyřmi navzájem shodnými rovnostrannými trojúhelníky, jedná se o pravidelný čtyřstěn (pravidelný tetraedr, viz obr.
Jak se pocita Ctyrboky jehlan
Objem jehlanu se spočítá jako obsah podstavy [Sp] krát výška jehlanu [v] lomeno třemi. Přičemž obsah podstavy [Sp] vypočítáme vzorcem pro obsah čtverce, tedy a2.
Jak se počítá objem : Vzorec pro výpočet objemu místnosti je tedy: V = a * b * c, kde a je délka, b je šířka a c je výška místnosti. Například, pokud má místnost délku 5 metrů, šířku 4 metry a výšku 3 metry, objem místnosti bude V = 5 * 4 * 3 = 60 metrů krychlových.
Stěny pravidelného čtyřstěnu jsou tvořeny čtyřmi shodnými rovnostrannými trojúhelníky. Toto těleso má čtyři vrcholy a šest hran, viz obr.
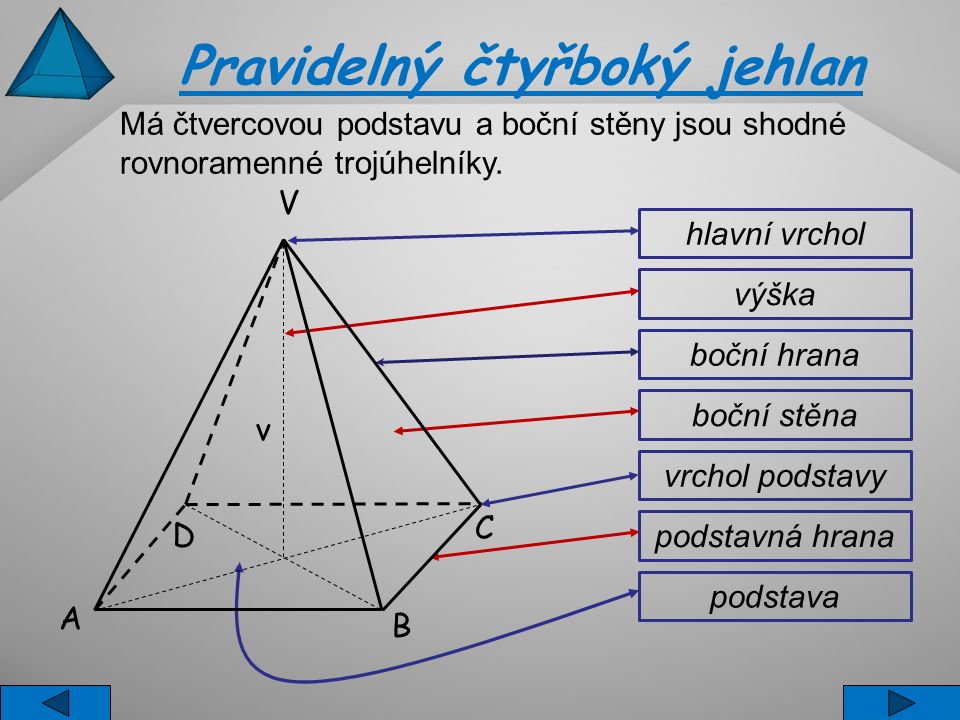
Povrch jehlanu
je součet obsahů všech jeho stěn. Obsah postavy vypočítám dle toho, o jaký obrazec se jedná – čtverec, pětiúhelník, šestiúhelník, apod. Plášť se pak skládá z několika trojúhelníků – vypočítám tedy obsah jednoho trojúhelníku (stěny) a následně jej vynásobím počtem trojúhelníků – stěn (dle podstavy).
Jak se počítá spl
Boční stěny hranolu tvoří plášť hranolu. Výškou hranolu je vzdálenost obou podstav. OBJEM hranolu vypočítáme jako součin obsahu podstavy (SP) a výšky hranolu (v). V = SP · v POVRCH hranolu je roven součtu obsahů obou podstav (SP) hranolu a obsahu pláště hranolu SPL (SPL = S1 + S2 + S3 + S4).NEJHLEDANĚJŠÍ PŘEVODY VELIČINY OBJEM
Změříme si vnitřní rozměry a vypočítáme podle známého vzorce objemu kvádru V = a*b*c. Při naměřené délce 150 cm, šířce 45 cm a hloubce 30 cm počítáme 150*45*30 = 202 500 cm³ = 202 l = 0,2 kubíků.
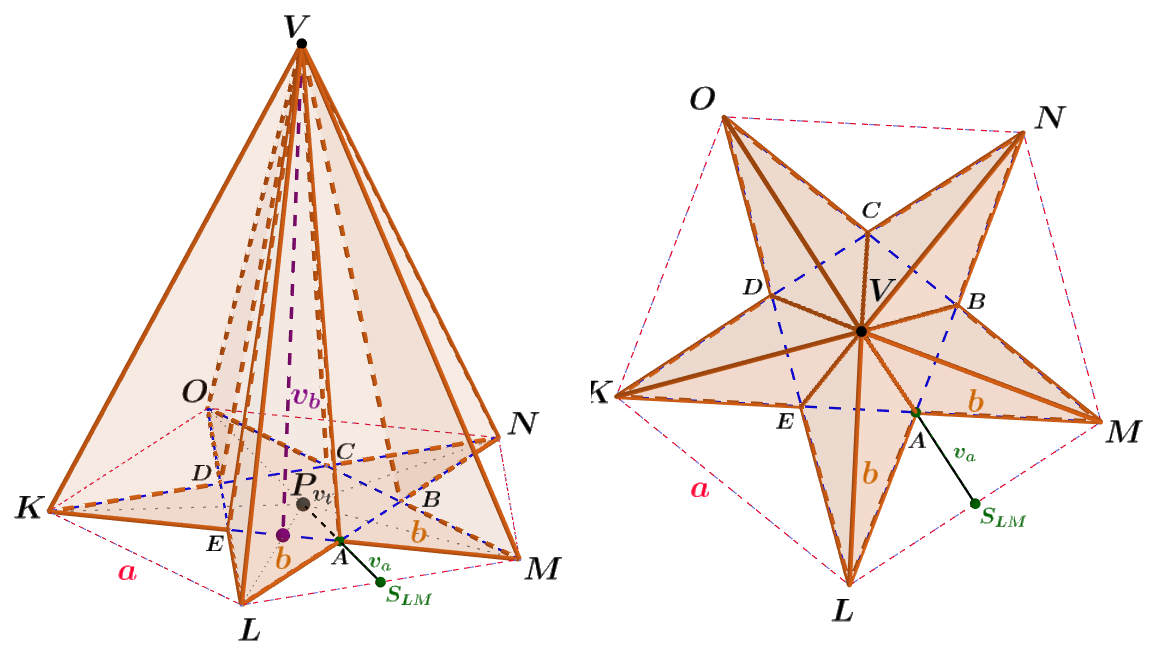
Pravidelný čtyřstěn je tvořen čtyřmi stejnými rovnostrannými trojúhelníky. Pravidelný čtyřstěn patří mezi takzvaná platónská tělesa. Pravidelný čtyřstěn je také trojrozměrným případem obecnějšího útvaru – simplexu. Spojením středů hran pravidelného čtyřstěnu vznikne pravidelný osmistěn vepsaný původnímu čtyřstěnu.
Kolik má kvádr hran : Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.
Jak Vypocitat povrch Pravidelneho Ctyrbokeho jehlanu : Povrch hranatých těles
Jehlan má jednu podstavu a plášť, povrch je tedy S = S p + S p l S=S_p+S_{pl} S=Sp+Spl. Stěny kvádru jsou obdélníky, přičemž vždy dvě jsou stejně velké. Povrch tedy vypočítáme jako S = 2 ( a b + a c + b c ) S = 2(ab+ac+bc) S=2(ab+ac+bc).
Jak Narysovat pravidelny Trojboky jehlan
Pravidelný trojboký hranol, jehlan
Podstavou je v obou případech rovnostranný trojúhelník. Výšku hranolu nanášíme v původní velikosti na boční hrany. Výšku jehlanu sestrojíme v těžišti trojúhelníku v původní velikosti.
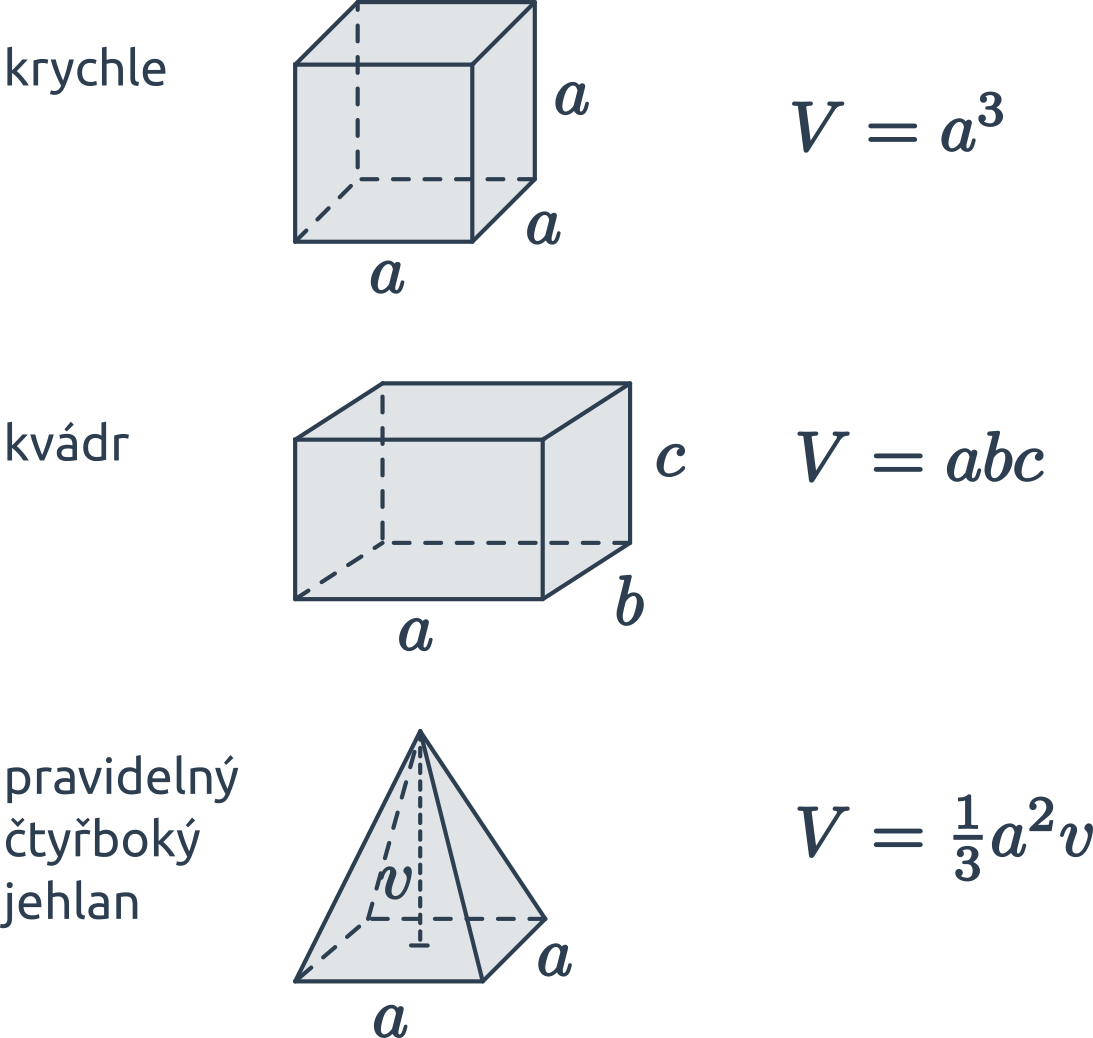
Povrch hranatých těles
Jehlan má jednu podstavu a plášť, povrch je tedy S = S p + S p l S=S_p+S_{pl} S=Sp+Spl. Stěny kvádru jsou obdélníky, přičemž vždy dvě jsou stejně velké. Povrch tedy vypočítáme jako S = 2 ( a b + a c + b c ) S = 2(ab+ac+bc) S=2(ab+ac+bc).Objem libovolného hranolu je součin obsahu podstavy a výšky: V = S p ⋅ v V=S_p\cdot v V=Sp⋅v. Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = a b c V = abc V=abc.
Kolik je čtvrt litru : Hájkova kronika uvádí jednotku věrtel jakožto jednotku užívanou pro kapaliny ve velikosti 1 věrtel = 248 litrů, což je 128 pint – což je tzv. pivní sud (jednotka). Ruská jednotka четверть (čtvrť) má přibližně 210 litrů.