– u velkých čísel budeme používat rozklad na součin prvočísel. U všech čísel provedeme rozklad na součin prvočísel.
Zakroužkujeme všechna společná prvočísla. Určíme největší společný dělitel (D) tak, že vynásobíme společná prvočísla.
24 = 2⋅ 2 2. ⋅ ⋅ 3.
⋅ 2 ⋅ 3 2 ⋅ 2.
D(24, 36) = 2 ⋅ 2 ⋅3 = 12.
Největší společný dělitel (NSD) dvou celých čísel je největší číslo, které beze zbytku dělí obě čísla. Příklady: NSD(18, 24) = 6, NSD(12, 21) = 3, NSD(24, 35) = 1.Nejmenší společný násobek dvou čísel lze nalézt tak, že každé z čísel je rozloženo na součin prvočísel (tzv. prvočíselný rozklad) a výsledný NSN je součinem největšího možného počtu všech prvočísel (resp. součin největších mocnin), která se vyskytují alespoň v jednom rozkladu.
Jak funguje euklidův algoritmus : Největší společný dělitel dvou přirozených čísel se ve středoškolských učebnicích obvykle počítá pomocí rozkladu obou čísel na prvočíselné činitele. Výsledek je pak součinem všech stejných činitelů (případně i vícenásobných) v rozkladech.
Kdy se pouziva nejvetsi spolecny Delitel
Největší společný dělitel se využívá při vytýkání a při řešení slovních úloh, kde řešíme například rozdělení různých květin do kytic, bonbónů do bonboniér nebo rozdělení plochy na stejně velké dílky.
Jak najít společný dělitel : Společný dělitel dvou nebo více přirozených čísel je každé přirozené číslo, jímž jsou všechna daná čísla dělitelná. Daná přirozená čísla mají vždy aspoň jednoho společného dělitele. Je jím číslo 1. Například číslo 3 je společným dělitelem čísel 18 a 30, číslo 5 jejich společným dělitelem není.
Zapíšeme n (3,4,5) = 60. Nejmenší společný násobek využíváme při hledání společného jmenovatele a při řešení slovních úloh, kde se například řeší stavba čtverce či obdélníku (krychle či kvádru) z různě velkých bloků; anebo úlohy kde, se hledá, kdy se znovu setkají vozidla, jež vyrážela ve stejný okamžik, a každému z nich objetí celé trasy …
Co musí splňovat algoritmus
hromadnost – algoritmus musí být aplikovatelný na určitou skupinu úloh, nikdy by neměl řešit jediný specifický problém, determinovanost neboli jednoznačnost – musí být přesně dané, co následuje po splnění určitého kroku, opakovatelnost – při zadání stejných vstupních dat musí algoritmus vrátit opět shodný výsledek.Algoritmus je popsán formalizovanou soustavou grafických symbolu. Používány vývojové diagramy nebo strukturogramy. Výhody: prehlednost, názornost, znázornení struktury problému, poskytuje informace o postupu jeho rešení. Jeden z nejcasteji používaných prostredku pro znázornování algoritmu.Nejmenší společný násobek využíváme při hledání společného jmenovatele a při řešení slovních úloh, kde se například řeší stavba čtverce či obdélníku (krychle či kvádru) z různě velkých bloků; anebo úlohy kde, se hledá, kdy se znovu setkají vozidla, jež vyrážela ve stejný okamžik, a každému z nich objetí celé trasy … nsn se používá například při sčítání nebo odčítání zlomků o různých jmenovatelích, kdy jmenovatel výsledku je nejmenším společným násobkem jmenovatelů sčítaných nebo odčítaných zlomků.
Jak najít všechny dělitele : Pravidla dělitelnosti
Číslo je dělitelné dvěmi, jestliže je sudé.
Číslo je dělitelné třemi, jestliže ciferný součet je dělitelný třemi.
Číslo je dělitelné čtyřmi, jestliže je poslední dvojčíslí dělitelné čtyřmi.
Číslo je dělitelné pěti, jestliže končí nulou nebo pětkou.
Jaký je Nejmenší společný násobek čísel 12 a 15 : Nejmenší společný násobek (NSN) dvou celých čísel je nejmenší číslo, které je beze zbytku dělitelné oběma čísly. Příklady: NSN(12, 15) = 60, NSN(6, 8) = 24, NSN(3, 15) = 15.
Jak najít společného jmenovatele
Postup hledání společného jmenovatele: ✓ Vyberte největšího jmenovatele a říkejte si jeho násobky (i jedna násobek ) ✓ Zastavte se ve chvíli, kdy tímto násobkem můžeme dělit druhého jmenovatele nebo všechny další jmenovatele (u více zlomků najednou) beze zbytku. ✓ Našli jste společného jmenovatele. Nejmenší společný násobek dvou nebo více přirozených čísel je nejmenší číslo ze všech společných násobků. Označuje se n (x, y).Algoritmus má alespoň jeden výstup, veličinu, která je v požadovaném vztahu k zadaným vstupům, a tím tvoří odpověď na problém, který algoritmus řeší (algoritmus vede od zpracování hodnot k výstupu) V praxi jsou proto předmětem zájmu hlavně takové algoritmy, které jsou v nějakém smyslu kvalitní.
Kdo vymyslel algoritmus : Samotný pojem algoritmus vzniknul zhruba o tisíc let později v 9. století našeho letopočtu, a je spojován se jménem perského matematika Abú Abd Alláh Muhammad ibn Músá al-Chwárizmí, který vytvořil systém arabských číslic.
Antwort Jak se najde nejvetsi spolecny Delitel? Weitere Antworten – Jak Vypocitat nejvetsi spolecny Nasobek
Největší společný dělitel (NSD) dvou celých čísel je největší číslo, které beze zbytku dělí obě čísla. Příklady: NSD(18, 24) = 6, NSD(12, 21) = 3, NSD(24, 35) = 1.Nejmenší společný násobek dvou čísel lze nalézt tak, že každé z čísel je rozloženo na součin prvočísel (tzv. prvočíselný rozklad) a výsledný NSN je součinem největšího možného počtu všech prvočísel (resp. součin největších mocnin), která se vyskytují alespoň v jednom rozkladu.

Jak funguje euklidův algoritmus : Největší společný dělitel dvou přirozených čísel se ve středoškolských učebnicích obvykle počítá pomocí rozkladu obou čísel na prvočíselné činitele. Výsledek je pak součinem všech stejných činitelů (případně i vícenásobných) v rozkladech.
Kdy se pouziva nejvetsi spolecny Delitel
Největší společný dělitel se využívá při vytýkání a při řešení slovních úloh, kde řešíme například rozdělení různých květin do kytic, bonbónů do bonboniér nebo rozdělení plochy na stejně velké dílky.
Jak najít společný dělitel : Společný dělitel dvou nebo více přirozených čísel je každé přirozené číslo, jímž jsou všechna daná čísla dělitelná. Daná přirozená čísla mají vždy aspoň jednoho společného dělitele. Je jím číslo 1. Například číslo 3 je společným dělitelem čísel 18 a 30, číslo 5 jejich společným dělitelem není.
Zapíšeme n (3,4,5) = 60.

Nejmenší společný násobek využíváme při hledání společného jmenovatele a při řešení slovních úloh, kde se například řeší stavba čtverce či obdélníku (krychle či kvádru) z různě velkých bloků; anebo úlohy kde, se hledá, kdy se znovu setkají vozidla, jež vyrážela ve stejný okamžik, a každému z nich objetí celé trasy …
Co musí splňovat algoritmus
hromadnost – algoritmus musí být aplikovatelný na určitou skupinu úloh, nikdy by neměl řešit jediný specifický problém, determinovanost neboli jednoznačnost – musí být přesně dané, co následuje po splnění určitého kroku, opakovatelnost – při zadání stejných vstupních dat musí algoritmus vrátit opět shodný výsledek.Algoritmus je popsán formalizovanou soustavou grafických symbolu. Používány vývojové diagramy nebo strukturogramy. Výhody: prehlednost, názornost, znázornení struktury problému, poskytuje informace o postupu jeho rešení. Jeden z nejcasteji používaných prostredku pro znázornování algoritmu.Nejmenší společný násobek využíváme při hledání společného jmenovatele a při řešení slovních úloh, kde se například řeší stavba čtverce či obdélníku (krychle či kvádru) z různě velkých bloků; anebo úlohy kde, se hledá, kdy se znovu setkají vozidla, jež vyrážela ve stejný okamžik, a každému z nich objetí celé trasy …
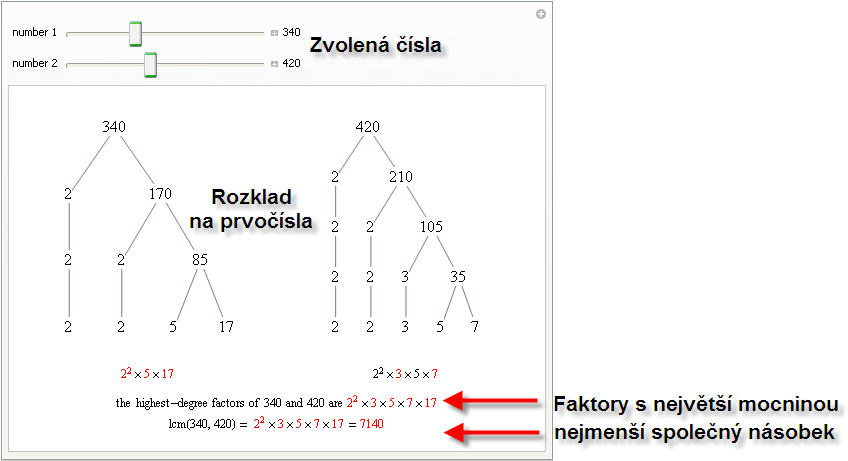
nsn se používá například při sčítání nebo odčítání zlomků o různých jmenovatelích, kdy jmenovatel výsledku je nejmenším společným násobkem jmenovatelů sčítaných nebo odčítaných zlomků.
Jak najít všechny dělitele : Pravidla dělitelnosti
Jaký je Nejmenší společný násobek čísel 12 a 15 : Nejmenší společný násobek (NSN) dvou celých čísel je nejmenší číslo, které je beze zbytku dělitelné oběma čísly. Příklady: NSN(12, 15) = 60, NSN(6, 8) = 24, NSN(3, 15) = 15.
Jak najít společného jmenovatele
Postup hledání společného jmenovatele: ✓ Vyberte největšího jmenovatele a říkejte si jeho násobky (i jedna násobek ) ✓ Zastavte se ve chvíli, kdy tímto násobkem můžeme dělit druhého jmenovatele nebo všechny další jmenovatele (u více zlomků najednou) beze zbytku. ✓ Našli jste společného jmenovatele.

Nejmenší společný násobek dvou nebo více přirozených čísel je nejmenší číslo ze všech společných násobků. Označuje se n (x, y).Algoritmus má alespoň jeden výstup, veličinu, která je v požadovaném vztahu k zadaným vstupům, a tím tvoří odpověď na problém, který algoritmus řeší (algoritmus vede od zpracování hodnot k výstupu) V praxi jsou proto předmětem zájmu hlavně takové algoritmy, které jsou v nějakém smyslu kvalitní.
Kdo vymyslel algoritmus : Samotný pojem algoritmus vzniknul zhruba o tisíc let později v 9. století našeho letopočtu, a je spojován se jménem perského matematika Abú Abd Alláh Muhammad ibn Músá al-Chwárizmí, který vytvořil systém arabských číslic.