Polorovinu lze znázornit např. pomocí rovnoběžného promítání, polorovina se zapisuje pomocí hraniční přímky a pomocného bodu se symbolem šipka. Opačná polorovina k dané polorovině je polorovina, která leží ve stejné rovině, má s danou polorovinou stejnou hraniční přímku, ale opačný směr.Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem.Přímka dělí rovinu na dvě navzájem opačné poloroviny a je jejich společnou hranicí (hraniční přímkou). Hraniční přímka patří do obou polorovin. Body, které neleží na hraniční přímce se nazývají vnitřní body.
Co je Polorovina čtverce : Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Tato přímka se nazývá hraniční. Polorovinu s hraniční přímkou p procházející bodem K značíme ↦ p K \mapsto pK ↦pK. Je-li přímka p určena body A, B, můžeme také psát ↦ A B K \mapsto ABK ↦ABK.
Jak vypadá přímka
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Jak se značí Mimoběžnost : Ve stereometrii rozlišujeme čtyři vzájemné polohy dvou přímek v prostoru.
Vzájemná poloha
Společné body
Značení
Rovnoběžné různé
žádné
p || q
Mimoběžné
žádné
p q
Různoběžné
jeden
p q
Totožné
všechny
p = q
POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí. Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem.
Co je to Polopřimka
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem.Lze tedy tedy přímka změřit POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.Lze tedy tedy přímka změřit POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí. POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
Jak určit vzájemnou polohu přímek : Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.
Jak vypadá polopřímka : POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
Co je to polopřímka jak se značí
POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí. POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.Sjednocením polopřímky a k ní opačné polopřímky vznikne přímka. Úsečka jako průsečík polopřímek.
Jak zjistit zda bod leží na přímce : Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC. AB = (1; -2; 2), AC = (-1; 2; -1).
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak se dělá polopřímka? Weitere Antworten – Jak zapsat Polorovinu
Polorovinu lze znázornit např. pomocí rovnoběžného promítání, polorovina se zapisuje pomocí hraniční přímky a pomocného bodu se symbolem šipka. Opačná polorovina k dané polorovině je polorovina, která leží ve stejné rovině, má s danou polorovinou stejnou hraniční přímku, ale opačný směr.Přímka – se zadává dvěma body, neboť každými dvěma body lze vést právě jednu přímku. Značíme ji dvěma body nebo častěji malým písmenem.Přímka dělí rovinu na dvě navzájem opačné poloroviny a je jejich společnou hranicí (hraniční přímkou). Hraniční přímka patří do obou polorovin. Body, které neleží na hraniční přímce se nazývají vnitřní body.
Co je Polorovina čtverce : Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Tato přímka se nazývá hraniční. Polorovinu s hraniční přímkou p procházející bodem K značíme ↦ p K \mapsto pK ↦pK. Je-li přímka p určena body A, B, můžeme také psát ↦ A B K \mapsto ABK ↦ABK.
Jak vypadá přímka
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Jak se značí Mimoběžnost : Ve stereometrii rozlišujeme čtyři vzájemné polohy dvou přímek v prostoru.
POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem.
Co je to Polopřimka
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem.Lze tedy tedy přímka změřit POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.Lze tedy tedy přímka změřit POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
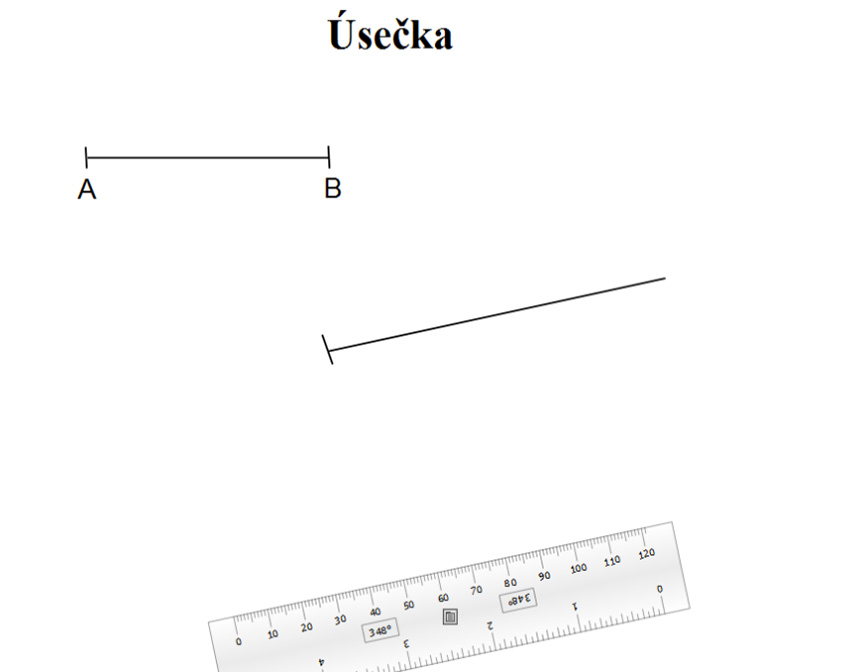
POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
Jak určit vzájemnou polohu přímek : Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.
Jak vypadá polopřímka : POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
Co je to polopřímka jak se značí
POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.
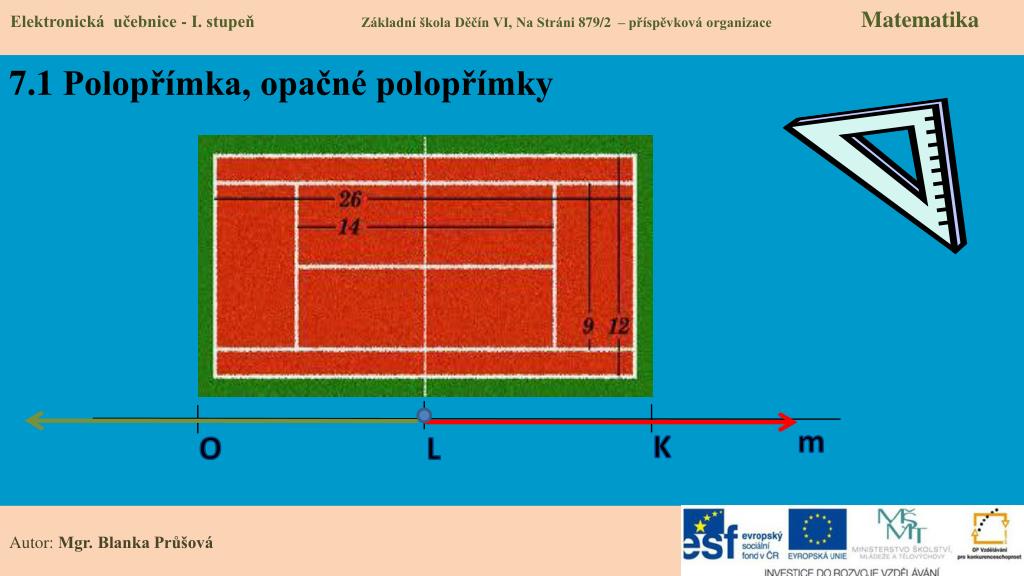
POLOPŘÍMKA je nekonečná rovná čára, která se nám nevejde ani do sešitu – proto do sešitu rýsujeme pouze její část!!! Narozdíl od přímky má ale svůj počáteční bod (značíme velkým tiskacím písmenem), můžeme tedy říci, že víme, že někde začíná, ale nikde nekončí.Sjednocením polopřímky a k ní opačné polopřímky vznikne přímka. Úsečka jako průsečík polopřímek.
Jak zjistit zda bod leží na přímce : Body A, B, C leží na jedné přímce, právě tehdy, když je vektor AB nenulovým reálným násobkem vektoru AC, tj. existuje nějaké reálné číslo k, pro které platí AB = kAC. AB = (1; -2; 2), AC = (-1; 2; -1).