V pravoúhlém trojuhelníku může sinus úhlu dosahovat hodnot mezi 0 až 1. Kosinus (cos): Kosinus úhlu v pravoúhlém trojúhelníku je definován jako poměr délky přilehlé strany k délce přepony trojúhelníka. V pravoúhlém trojuhelníku může kosinus úhlu dosahovat hodnot mezi 0 až 1.Hodnoty sinus na jednotkové kružnici
x (úhel)
45°
π/4
1/8
135°
3π/4
3/8
60°
π/3
1/6
120°
2π/3
1/3
Když se podíváte na graf funkce sinus a cosinus současně, tak zjistíte, že se od sebe moc neliší, že jedna je jen trochu posunutá oproti té druhé. A naopak, pokud u cosinu odečteme π/2, dostaneme sinus.
Jak se počítá sinus na kalkulačce : Před stiskem samotné klávesy sin, cos nebo tan, je třeba stisknout klávesu, která bývá označena symbolem INV, Shift, 2nd, nebo f–1. Inverzní funkce k sin bývá označována sin–1 nebo arcsin. Inverzní funkce ke cos se značí cos–1 nebo arccos. Inverzní funkce k tan se označuje tan–1 nebo arctan.
Kolik je cos 30
X [º]
X [rad]
cos(x)
28
0,4887
0,8829
29
0,5061
0,8746
30
0,5236
0,8660
31
0,5411
0,8572
Jak se počítá sinova věta : Jsou to tyto: Sinovou větu můžeme také vyjádřit ve tvaru , tj. poměr délek dvou stran v trojúhelníku se rovná poměru velikostí sinů protilehlých úhlů k těmto stranám.
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně: Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony. Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Kosinus ( cos) úhlu α je poměr délky odvěsny přilehlé úhlu α a délky přepony.
Kolik je sinus 90 stupňů
sin(90) = sin(2.035rad) = 0.8939.
X [º]
X [rad]
sin(x)
23
0,4014
0,3907
24
0,4189
0,4067
25
0,4363
0,4226
26
0,4538
0,4384
Pokud tento úhel naskládáte do kalkulačky a vypočítáte sinus, získáte právě 0 , 6 0,6 0,6 (po drobném zaokrouhlení). K čemu je to dobré Je to dobré v případě, kdy znáte jeden úhel a délku jedné strany a potřebujete dopočítat zbývající strany. Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.
Jak zni sinus : Toto je sinus, funkce sinus. Toto je funkce kosinus a tady funkce tangens. Zkráceně zapisujeme sin, cos nebo tan (tg). A tyto funkce vyjadřují pro každý úhel v tomto trojúhelníku určité poměry stran.
Kdy se pouziva sinova a kdy Kosinová věta : Vedle sinové věty si v obecném trojúhelníku zopakujeme také větu kosinovou. Použijeme ji například, máme-li dvě strany a úhel jimi sevřený, a tím snadno dopočítáme třetí stranu. Na zbylé úhly pak využijeme známou sinovou větu a trojúhelník tak dopočítáme.
Co je sinus a cosinus
Druhou souřadnici bodu jednotkové kružnice na koncovém rameni orientovaného úhlu v základní poloze nazýváme sinus a jeho první souřadnici nazveme kosinus . Jsou to tyto: Sinovou větu můžeme také vyjádřit ve tvaru , tj. poměr délek dvou stran v trojúhelníku se rovná poměru velikostí sinů protilehlých úhlů k těmto stranám.Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0. Pro α z ⟨π/2,π⟩ definujeme sin(α) = sin(π − α) a cos(α) = −cos(π − α). Pro α z ⟨π,2π⟩ definujeme sin(α) = −sin(α − π) a cos(α) = −cos(2π − α).
Kdy používáme sinovou větu : Věta se používá zejména v následujících dvou případech: Jsou dány dva úhly trojúhelníku a délku jedné jeho strany a mají se dopočítat velikosti zbývajících stran. To je typická úloha při triangulaci. Jsou známy délky dvou stran trojúhelníku a velikost vnitřního úhlu který nesvírají, a je třeba zjistit zbývající úhly.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak počítat sinus a kosinus? Weitere Antworten – Jak se počítá sinus a kosinus
V pravoúhlém trojuhelníku může sinus úhlu dosahovat hodnot mezi 0 až 1. Kosinus (cos): Kosinus úhlu v pravoúhlém trojúhelníku je definován jako poměr délky přilehlé strany k délce přepony trojúhelníka. V pravoúhlém trojuhelníku může kosinus úhlu dosahovat hodnot mezi 0 až 1.Hodnoty sinus na jednotkové kružnici
Když se podíváte na graf funkce sinus a cosinus současně, tak zjistíte, že se od sebe moc neliší, že jedna je jen trochu posunutá oproti té druhé. A naopak, pokud u cosinu odečteme π/2, dostaneme sinus.
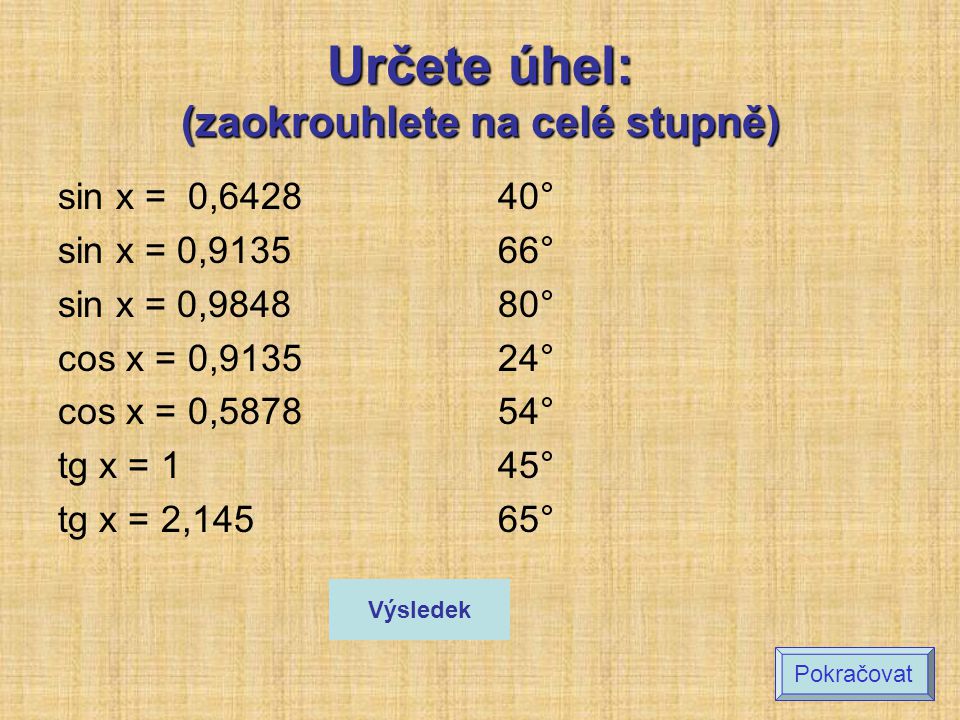
Jak se počítá sinus na kalkulačce : Před stiskem samotné klávesy sin, cos nebo tan, je třeba stisknout klávesu, která bývá označena symbolem INV, Shift, 2nd, nebo f–1. Inverzní funkce k sin bývá označována sin–1 nebo arcsin. Inverzní funkce ke cos se značí cos–1 nebo arccos. Inverzní funkce k tan se označuje tan–1 nebo arctan.
Kolik je cos 30
Jak se počítá sinova věta : Jsou to tyto: Sinovou větu můžeme také vyjádřit ve tvaru , tj. poměr délek dvou stran v trojúhelníku se rovná poměru velikostí sinů protilehlých úhlů k těmto stranám.
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně: Sinus ( sin) úhlu α je poměr délky odvěsny protilehlé úhlu α a délky přepony.
Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
Kolik je sinus 90 stupňů
sin(90) = sin(2.035rad) = 0.8939.
Pokud tento úhel naskládáte do kalkulačky a vypočítáte sinus, získáte právě 0 , 6 0,6 0,6 (po drobném zaokrouhlení). K čemu je to dobré Je to dobré v případě, kdy znáte jeden úhel a délku jedné strany a potřebujete dopočítat zbývající strany.
Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0.
Jak zni sinus : Toto je sinus, funkce sinus. Toto je funkce kosinus a tady funkce tangens. Zkráceně zapisujeme sin, cos nebo tan (tg). A tyto funkce vyjadřují pro každý úhel v tomto trojúhelníku určité poměry stran.
Kdy se pouziva sinova a kdy Kosinová věta : Vedle sinové věty si v obecném trojúhelníku zopakujeme také větu kosinovou. Použijeme ji například, máme-li dvě strany a úhel jimi sevřený, a tím snadno dopočítáme třetí stranu. Na zbylé úhly pak využijeme známou sinovou větu a trojúhelník tak dopočítáme.
Co je sinus a cosinus
Druhou souřadnici bodu jednotkové kružnice na koncovém rameni orientovaného úhlu v základní poloze nazýváme sinus a jeho první souřadnici nazveme kosinus .
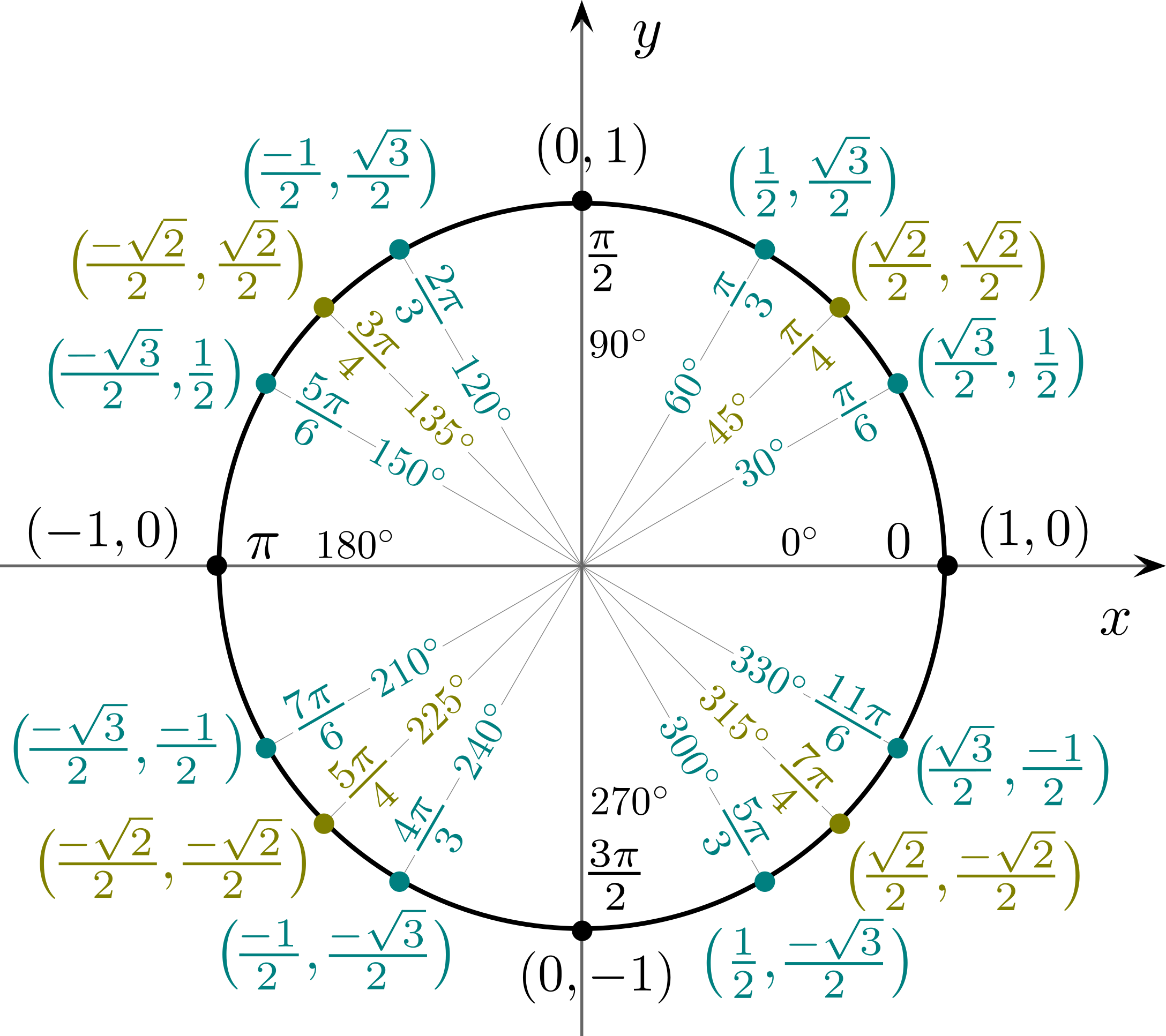
Jsou to tyto: Sinovou větu můžeme také vyjádřit ve tvaru , tj. poměr délek dvou stran v trojúhelníku se rovná poměru velikostí sinů protilehlých úhlů k těmto stranám.Nejprve definujeme sin(0) = 0, cos(0) = 1, sin(π/2) = 1, cos(π/2) = 0. Pro α z ⟨π/2,π⟩ definujeme sin(α) = sin(π − α) a cos(α) = −cos(π − α). Pro α z ⟨π,2π⟩ definujeme sin(α) = −sin(α − π) a cos(α) = −cos(2π − α).
Kdy používáme sinovou větu : Věta se používá zejména v následujících dvou případech: Jsou dány dva úhly trojúhelníku a délku jedné jeho strany a mají se dopočítat velikosti zbývajících stran. To je typická úloha při triangulaci. Jsou známy délky dvou stran trojúhelníku a velikost vnitřního úhlu který nesvírají, a je třeba zjistit zbývající úhly.