Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak poznat trojúhelník podle stran : RŮZNOSTRANNÝ (obecný) TROJÚHELNÍK je trojúhelník, jehož žádné dvě strany nemají stejnou délku. a = b + c ROVNORAMENNÝ TROJÚHELNÍK je trojúhelník, jehož dvě strany jsou stejně dlouhé. trojúhelník, jehož všechny strany mají stejnou délku.
Jak najít střed kružnice
Označte střed tečkou nebo křížkem. To bude váš výchozí bod. Nakreslete dvě čáry od této tečky na obě strany kruhu, jednu čáru rovnoběžnou s horním a dolním okrajem a jednu čáru rovnoběžnou s levým a pravým okrajem. V místě, kde se tyto dvě čáry protínají, najdete středový bod.
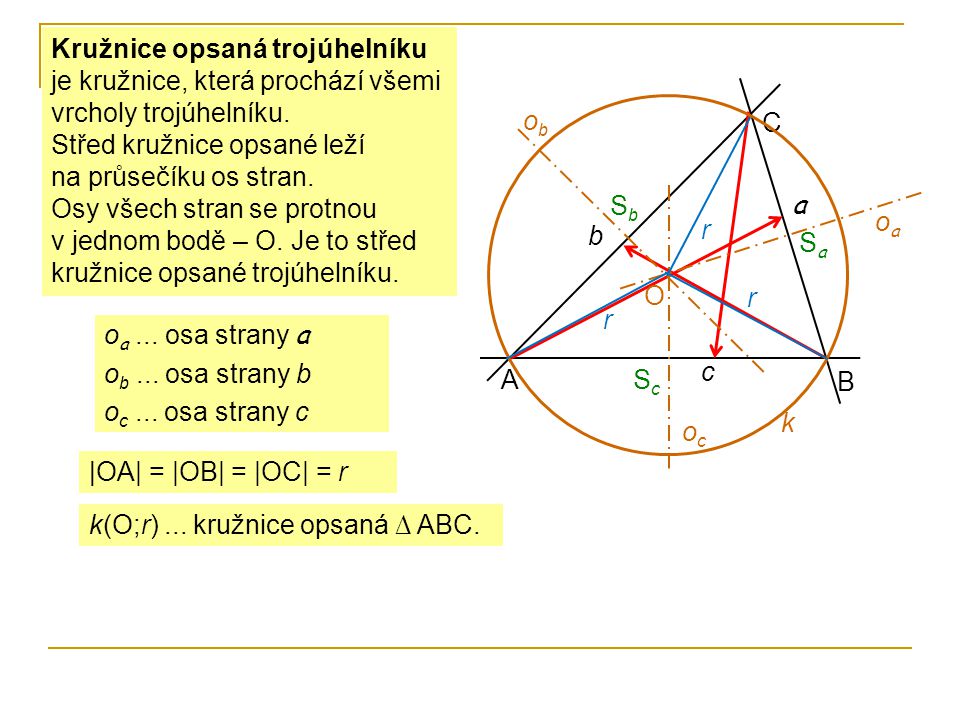
Co je střed trojúhelníku : Střed kružnice opsané trojúhelníku je průsečík os stran trojúhelníku, poloměr se rovná vzdálenosti středu od libovolného vrcholu.
Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Trojúhelník je polovinou obsahu obdélníka, proto obsah trojúhelníka je jedna polovina x strana x výška (straně odpovídající): Pro výpočet obsahu trojúhelníka je možno použít libovolnou stranu s odpovídající výškou. Není ale možné použít stranu v kombinaci s jinou výškou.
Jak zjistit Preponu
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.Strany se označují malými tiskacími či psacími písmeny, případně malými tiskacími či psacími písmeny s indexem vpravo dole. (např. a, b, c, d, a1, a2, …) Pro označení stran platí pravidlo, že strana je pojmenována podle protilehlého vrcholu.
Rozdělení trojúhelníků podle velikosti úhlů Podle velikosti vnitřních úhlů dělíme trojúhelníky na: ostroúhlé, tupoúhlé, pravoúhlé. U pravoúhlého trojúhelníka ještě pojmenováváme jeho strany – má dvě odvěsny (červeně) a naproti pravému úhlu se strana jmenuje přepona (fialově).
Jak se Sestrojuje střed kružnice : Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku. Máme trojúhelník ABC. Průsečík os o1 a o2 je střed S kružnice opsané k. Tuto kružnici sestrojíme, její poloměr je dán vzdáleností středu S a libovolného vrcholu.
Co je Středná kružnic : Definice (Stredná) Spojnice stredu dvou kružnic se nazývá jejich stredná.
Jak zjistit třetí stranu trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Rozdělení trojúhelníků podle velikosti úhlů Podle velikosti vnitřních úhlů dělíme trojúhelníky na: ostroúhlé, tupoúhlé, pravoúhlé. U pravoúhlého trojúhelníka ještě pojmenováváme jeho strany – má dvě odvěsny (červeně) a naproti pravému úhlu se strana jmenuje přepona (fialově).Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak se pocita přepona : Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak najít střed strany trojúhelníku? Weitere Antworten – Jak najít střed trojúhelníku
Střed kružnice vepsané je průsečíkem všech 3 os úhlů trojúhelníku. Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.
Jak poznat trojúhelník podle stran : RŮZNOSTRANNÝ (obecný) TROJÚHELNÍK je trojúhelník, jehož žádné dvě strany nemají stejnou délku. a = b + c ROVNORAMENNÝ TROJÚHELNÍK je trojúhelník, jehož dvě strany jsou stejně dlouhé. trojúhelník, jehož všechny strany mají stejnou délku.
Jak najít střed kružnice
Označte střed tečkou nebo křížkem. To bude váš výchozí bod. Nakreslete dvě čáry od této tečky na obě strany kruhu, jednu čáru rovnoběžnou s horním a dolním okrajem a jednu čáru rovnoběžnou s levým a pravým okrajem. V místě, kde se tyto dvě čáry protínají, najdete středový bod.
Co je střed trojúhelníku : Střed kružnice opsané trojúhelníku je průsečík os stran trojúhelníku, poloměr se rovná vzdálenosti středu od libovolného vrcholu.
Platí Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Délku přepony pravoúhlého trojúhelníku vypočteme podle vzorce c2 = a2 + b2.
Trojúhelník je polovinou obsahu obdélníka, proto obsah trojúhelníka je jedna polovina x strana x výška (straně odpovídající): Pro výpočet obsahu trojúhelníka je možno použít libovolnou stranu s odpovídající výškou. Není ale možné použít stranu v kombinaci s jinou výškou.
Jak zjistit Preponu
Přepona pravoúhlého trojúhelníku je vždy ta strana, která se nachází naproti pravému úhlu. Tato strana je v trojúhelníku nejdelší. Další dvě strany jsou nazvány protilehlá a přilehlá odvěsna.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.Strany se označují malými tiskacími či psacími písmeny, případně malými tiskacími či psacími písmeny s indexem vpravo dole. (např. a, b, c, d, a1, a2, …) Pro označení stran platí pravidlo, že strana je pojmenována podle protilehlého vrcholu.
Rozdělení trojúhelníků podle velikosti úhlů Podle velikosti vnitřních úhlů dělíme trojúhelníky na: ostroúhlé, tupoúhlé, pravoúhlé. U pravoúhlého trojúhelníka ještě pojmenováváme jeho strany – má dvě odvěsny (červeně) a naproti pravému úhlu se strana jmenuje přepona (fialově).
Jak se Sestrojuje střed kružnice : Střed kružnice opsané je průsečíkem všech 3 os stran trojúhelníku. Máme trojúhelník ABC. Průsečík os o1 a o2 je střed S kružnice opsané k. Tuto kružnici sestrojíme, její poloměr je dán vzdáleností středu S a libovolného vrcholu.
Co je Středná kružnic : Definice (Stredná) Spojnice stredu dvou kružnic se nazývá jejich stredná.
Jak zjistit třetí stranu trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Rozdělení trojúhelníků podle velikosti úhlů Podle velikosti vnitřních úhlů dělíme trojúhelníky na: ostroúhlé, tupoúhlé, pravoúhlé. U pravoúhlého trojúhelníka ještě pojmenováváme jeho strany – má dvě odvěsny (červeně) a naproti pravému úhlu se strana jmenuje přepona (fialově).Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak se pocita přepona : Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami. Pythagorovu větu můžeme zapsat vztahem c 2 = a 2 + b 2 c^2 = a^2 + b^2 c2=a2+b2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b.