Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.SEČNA KRUŽNICE je přímka, která má s kružnicí společné právě dva různé body.⇒ Kritérium rovnoběžnosti přímky a roviny: Přímka p je rovnoběžná s rovinou ρ , jestliže v rovině ρ leží alespoň jedna přímka p′, která je s přímkou p rovnoběžná.
Kdy jsou přímky totožné : Dvě přímky p(P, u) a q(Q, v) jsou totožné právě tehdy, jsou-li rovnoběžné a leží-li bod Q na přímce p. Jsou-li přímky p(P, u) a q(Q, v) totožné, pak jsou rovnoběžné (u je násobkem v) a bod Q leží na přímce p.
Jak vypočítat vzájemnou polohu přímek
Vzájemná poloha přímek v prostoru
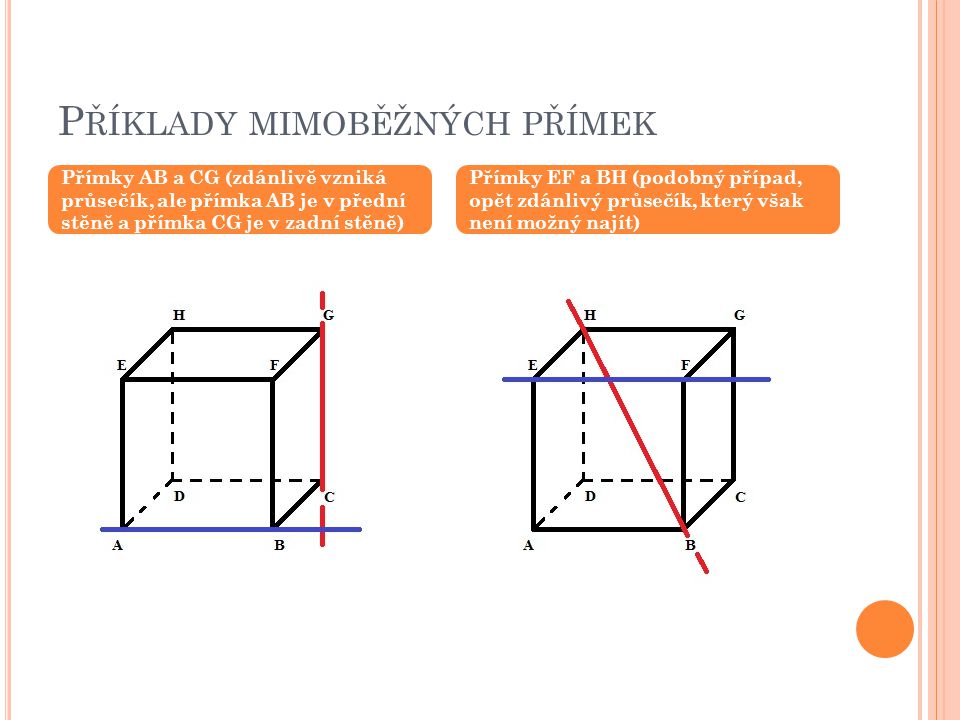
p ∩ q = ∅ Pokud přímky p a q nemají žádný společný bod, mohou být rovnoběžné různé nebo mimoběžné.
p ∩ q = {P} Přímky p a q jsou různoběžné, mají jeden společný bod P.
p ∩ q = p. Přímky p a q jsou totožné.
Jak vypočítat vzdálenost dvou přímek : Vzdálenost dvou mimoběžných přímek je rovna minimální vzdálenosti kterýchkoliv dvou jejich bodů. Dvojice bodů, která určuje tuto vzdálenost, je právě jedna. Jsou to body X[x1; x2; x3] na přímce p a Y[y1; y2; y3] na přímce q takové, že přímka XY je kolmá jak na přímku p, tak na přímku q.
Kruh a kružnice
U každého bodu v rovině pak můžeme určit, kde leží: na kružnici (jejich vzdálenost od S je rovna r) ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici) ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici) Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
Kdy je přímka kolmá k rovině
Přímka a rovina jsou k sobě kolmé právě tehdy, když je přímka kolmá ke všem přímkám roviny.Definice: Nemá-li přímka s rovinou žádný společný bod, pak říkáme, že jsou rovnoběžné. Pokud přímka leží v rovině, pak je také považujeme za rovnoběžné. Věta: Je-li přímka a rovnoběžná s přímkou b a přímka b rovnoběžná s rovinou , je přímka a rovnoběžná s rovinou .Pokud známe směrový vektor nebo normálový vektor, pak můžeme určit vzájemnou polohu přímek. Přitom platí: Pokud jsou směrové vektory kolineární (lineárně závislé), pak jsou přímky rovnoběžné nebo shodné. Pokud nejsou směrové vektory kolineární (lineárně závislé), pak jsou přímky různoběžné. Kruh a kružnice
U každého bodu v rovině pak můžeme určit, kde leží: na kružnici (jejich vzdálenost od S je rovna r) ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici) ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici)
Jak vypadají kolmé přímky : Kolmice je přímka, která protíná jinou přímku a svírá s ní úhel 90°. Kolmost přímek p a q zapisujeme p ⊥ q p \perp q p⊥q. Dvě přímky, které jsou kolmé na nějakou třetí přímku a současně obě leží v jedné rovině, jsou rovnoběžky.
Jak se vyznačuje přímka : Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Kdy jsou roviny kolmé
Definice: Dvě roviny jsou kolmé, jestliže jejich odchylka je 90°. Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
Kdy jsou přímky kolmé : Kolmice je geometrický útvar. Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jaká může být vzájemná poloha přímek v prostoru? Weitere Antworten – Co je to vzájemná poloha přímek
Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.SEČNA KRUŽNICE je přímka, která má s kružnicí společné právě dva různé body.⇒ Kritérium rovnoběžnosti přímky a roviny: Přímka p je rovnoběžná s rovinou ρ , jestliže v rovině ρ leží alespoň jedna přímka p′, která je s přímkou p rovnoběžná.
Kdy jsou přímky totožné : Dvě přímky p(P, u) a q(Q, v) jsou totožné právě tehdy, jsou-li rovnoběžné a leží-li bod Q na přímce p. Jsou-li přímky p(P, u) a q(Q, v) totožné, pak jsou rovnoběžné (u je násobkem v) a bod Q leží na přímce p.
Jak vypočítat vzájemnou polohu přímek
Vzájemná poloha přímek v prostoru
Jak vypočítat vzdálenost dvou přímek : Vzdálenost dvou mimoběžných přímek je rovna minimální vzdálenosti kterýchkoliv dvou jejich bodů. Dvojice bodů, která určuje tuto vzdálenost, je právě jedna. Jsou to body X[x1; x2; x3] na přímce p a Y[y1; y2; y3] na přímce q takové, že přímka XY je kolmá jak na přímku p, tak na přímku q.
Kruh a kružnice
U každého bodu v rovině pak můžeme určit, kde leží: na kružnici (jejich vzdálenost od S je rovna r) ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici) ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici)
Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
Kdy je přímka kolmá k rovině
Přímka a rovina jsou k sobě kolmé právě tehdy, když je přímka kolmá ke všem přímkám roviny.Definice: Nemá-li přímka s rovinou žádný společný bod, pak říkáme, že jsou rovnoběžné. Pokud přímka leží v rovině, pak je také považujeme za rovnoběžné. Věta: Je-li přímka a rovnoběžná s přímkou b a přímka b rovnoběžná s rovinou , je přímka a rovnoběžná s rovinou .Pokud známe směrový vektor nebo normálový vektor, pak můžeme určit vzájemnou polohu přímek. Přitom platí: Pokud jsou směrové vektory kolineární (lineárně závislé), pak jsou přímky rovnoběžné nebo shodné. Pokud nejsou směrové vektory kolineární (lineárně závislé), pak jsou přímky různoběžné.
Kruh a kružnice
U každého bodu v rovině pak můžeme určit, kde leží: na kružnici (jejich vzdálenost od S je rovna r) ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici) ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici)
Jak vypadají kolmé přímky : Kolmice je přímka, která protíná jinou přímku a svírá s ní úhel 90°. Kolmost přímek p a q zapisujeme p ⊥ q p \perp q p⊥q. Dvě přímky, které jsou kolmé na nějakou třetí přímku a současně obě leží v jedné rovině, jsou rovnoběžky.
Jak se vyznačuje přímka : Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.
Kdy jsou roviny kolmé
Definice: Dvě roviny jsou kolmé, jestliže jejich odchylka je 90°.
Přímka je jednorozměrný základní geometrický útvar. Lze ji popsat jako nekonečně tenkou, dvoustranně nekonečně dlouhou, dokonale rovnou křivku (pojem křivka v matematice zahrnuje i „rovné křivky“), tedy křivku s nekonečně velkým poloměrem zakřivení.Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.
Kdy jsou přímky kolmé : Kolmice je geometrický útvar. Je to přímka, která protíná jinou přímku a svírá s ní pravý úhel, tedy úhel 90°. Přímky jsou kolmé na sebe navzájem. Pokud je jedna kolmá na druhou, je druhá kolmá na první.