Útvar označujeme za osově souměrný, pokud je v nějaké osové souměrnosti obrazem sebe sama. Osu této souměrnosti pak nazýváme osou útvaru. Obrázek uvádí příklady útvarů osově souměrných (zelené, s vyznačenými osami souměrnosti) i těch nesouměrných (červené):Je dána základní abeceda (A, B, C, D, E, F, G, H, CH, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z). Kolik samohlásek je osově souměrnýchOsové souměrnosti v rovině jsou důležité, protože každá shodnost v rovině se dá složit z nejvýše tří osových souměrností. Osovou souměrnost lze definovat i v euklidovském prostoru vyšších dimenzí, nazývá se pak obecně souměrnost podle přímky.
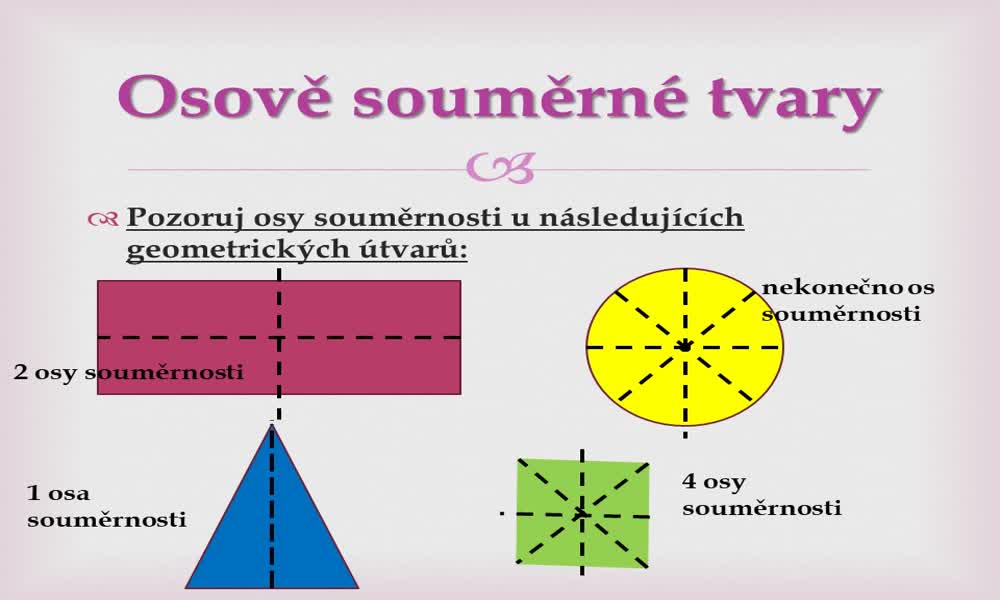
Kolik má obdélník os souměrnosti : Obdélník je v obecném případě osově souměrný podle dvou os. Osami souměrnosti jsou rovnoběžky se stranami procházející průsečíkem úhlopříček. Speciální případ obdélníku – čtverec – je osově souměrný podle čtyř os, dalšími dvěma osami jsou jeho úhlopříčky.
Co je to osově souměrné
Jestliže souměrnost podle osy převádí útvar U ve stejný útvar U ′ = U, říkáme, že útvar U je souměrný podle osy, nebo také že je osově souměrný.
Jak se značí osová souměrnost : Těžnice označujeme obvykle malým písmenem t s indexem názvu strany, ke které příslušná těžnice patří. Geometrický útvar je osově souměrný útvar, jestliže ho lze rozdělit přímkou na dvě shodné části. Taková přímka se nazývá osa souměrnosti a značí se o.
a protilehlé strany jsou rovnoběžné. , které se navzájem půlí a jsou na sebe kolmé. Kosočtverec má dvě osy souměrnosti, kterými jsou úhlopříčky, a jeden střed souměrnosti, kterým je průsečík úhlopříček. HLEDÁNÍ SOUMĚRNOSTI
Úkol je jednoduchý – najít přírodniny, tvary, předměty a určit u nich, zda někde jsou osově souměrné či ne. Dle času se můžete domluvit na počtu věcí (například 5 + 5 věcí). Na jednu vhodnou přírodninu mohou děti i zakreslit osu souměrnosti a pak dle osy rozstřihnout a nalepit do pracovního listu.
Jak se rýsuje osová souměrnost
Pokud to rýsujete, použijte kružítko (zapíchněte ho do průsečíku osy a kolmice a udělejte kružnici procházející bodem A ). Pokud označíme průsečík osy o a kolmice q jako S , tak musí platit |AS| = |A'S| .Osově souměrný útvar je takový útvar, který se podle nějaké své osy zobrazí sám na sebe. Mezi osově souměrné útvary patří například rovnostranný trojúhelník, čtverec, kosočtverec, obdélník, kružnice.Odpovídající si body leží na kolmici k ose souměrnosti v opačných polorovinách a ve stejné vzdálenosti od osy. Osovou souměrnost můžeme zapsat: O(o): A → A'. Čteme: obrazem bodu A v osové souměrnosti je bod . Body ležící na ose souměrnosti nazýváme samodružné (X = X'), vzor a obraz jsou totožné. Středová souměrnost S(S) se středem v bodě S je zobrazení v rovině, ve kterém se zobrazí bod S na bod S'=S a každý bod X \neq S na bod X' tak, že bod S je středem úsečky XX'. Tedy platí, že |XS|=|SX'|. Bod S se nazývá střed souměrnosti.
Jak poznat středově souměrný útvar : Středově souměrný útvar
Útvar označujeme za středově souměrný, pokud je v nějaké středové souměrnosti obrazem sebe sama. Střed této středové souměrnosti pak nazýváme středem souměrnosti objektu.
Co jsou středově souměrné útvary : Mezi středově souměrné útvary patří například čtverec, kosočtverec, kružnice, obdélník nebo kosodélník. Středem souměrnosti kružnice je její střed, středem souměrnosti ostatních vyjmenovaných útvarů je průsečík jejich úhlopříček.
Které útvary mají střed souměrnosti
Mezi středově souměrné útvary patří například čtverec, kosočtverec, kružnice, obdélník nebo kosodélník. Středová souměrnost se středem S je shodné zobrazení, které každému bodu X (které leží mimo bod S) přiřazuje bod X' tak, že bod S je středem úsečky XX'.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jaké jsou osově souměrné útvary? Weitere Antworten – Jak vysvětlit osovou souměrnost
Osově souměrný útvar
Útvar označujeme za osově souměrný, pokud je v nějaké osové souměrnosti obrazem sebe sama. Osu této souměrnosti pak nazýváme osou útvaru. Obrázek uvádí příklady útvarů osově souměrných (zelené, s vyznačenými osami souměrnosti) i těch nesouměrných (červené):Je dána základní abeceda (A, B, C, D, E, F, G, H, CH, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z). Kolik samohlásek je osově souměrnýchOsové souměrnosti v rovině jsou důležité, protože každá shodnost v rovině se dá složit z nejvýše tří osových souměrností. Osovou souměrnost lze definovat i v euklidovském prostoru vyšších dimenzí, nazývá se pak obecně souměrnost podle přímky.
Kolik má obdélník os souměrnosti : Obdélník je v obecném případě osově souměrný podle dvou os. Osami souměrnosti jsou rovnoběžky se stranami procházející průsečíkem úhlopříček. Speciální případ obdélníku – čtverec – je osově souměrný podle čtyř os, dalšími dvěma osami jsou jeho úhlopříčky.
Co je to osově souměrné
Jestliže souměrnost podle osy převádí útvar U ve stejný útvar U ′ = U, říkáme, že útvar U je souměrný podle osy, nebo také že je osově souměrný.
Jak se značí osová souměrnost : Těžnice označujeme obvykle malým písmenem t s indexem názvu strany, ke které příslušná těžnice patří. Geometrický útvar je osově souměrný útvar, jestliže ho lze rozdělit přímkou na dvě shodné části. Taková přímka se nazývá osa souměrnosti a značí se o.
a protilehlé strany jsou rovnoběžné. , které se navzájem půlí a jsou na sebe kolmé. Kosočtverec má dvě osy souměrnosti, kterými jsou úhlopříčky, a jeden střed souměrnosti, kterým je průsečík úhlopříček.
HLEDÁNÍ SOUMĚRNOSTI
Úkol je jednoduchý – najít přírodniny, tvary, předměty a určit u nich, zda někde jsou osově souměrné či ne. Dle času se můžete domluvit na počtu věcí (například 5 + 5 věcí). Na jednu vhodnou přírodninu mohou děti i zakreslit osu souměrnosti a pak dle osy rozstřihnout a nalepit do pracovního listu.
Jak se rýsuje osová souměrnost
Pokud to rýsujete, použijte kružítko (zapíchněte ho do průsečíku osy a kolmice a udělejte kružnici procházející bodem A ). Pokud označíme průsečík osy o a kolmice q jako S , tak musí platit |AS| = |A'S| .Osově souměrný útvar je takový útvar, který se podle nějaké své osy zobrazí sám na sebe. Mezi osově souměrné útvary patří například rovnostranný trojúhelník, čtverec, kosočtverec, obdélník, kružnice.Odpovídající si body leží na kolmici k ose souměrnosti v opačných polorovinách a ve stejné vzdálenosti od osy. Osovou souměrnost můžeme zapsat: O(o): A → A'. Čteme: obrazem bodu A v osové souměrnosti je bod . Body ležící na ose souměrnosti nazýváme samodružné (X = X'), vzor a obraz jsou totožné.
Středová souměrnost S(S) se středem v bodě S je zobrazení v rovině, ve kterém se zobrazí bod S na bod S'=S a každý bod X \neq S na bod X' tak, že bod S je středem úsečky XX'. Tedy platí, že |XS|=|SX'|. Bod S se nazývá střed souměrnosti.
Jak poznat středově souměrný útvar : Středově souměrný útvar
Útvar označujeme za středově souměrný, pokud je v nějaké středové souměrnosti obrazem sebe sama. Střed této středové souměrnosti pak nazýváme středem souměrnosti objektu.
Co jsou středově souměrné útvary : Mezi středově souměrné útvary patří například čtverec, kosočtverec, kružnice, obdélník nebo kosodélník. Středem souměrnosti kružnice je její střed, středem souměrnosti ostatních vyjmenovaných útvarů je průsečík jejich úhlopříček.
Které útvary mají střed souměrnosti
Mezi středově souměrné útvary patří například čtverec, kosočtverec, kružnice, obdélník nebo kosodélník.
Středová souměrnost se středem S je shodné zobrazení, které každému bodu X (které leží mimo bod S) přiřazuje bod X' tak, že bod S je středem úsečky XX'.