1+99=3+97=5+95=100. Obecně se dá říci, že ve dvojici jsou čísla k a 100−k, takže jejich součet je opravdu 100. Lichých čísel je polovina ze všech celých čísel od 1 do 100, tedy 50, a z nich vytvoříme 25 dvojic, každou se součtem 100. Celkový součet všech kladných lichých čísel menších než 100 je tedy 2500.Když děti učí telka! Naučme se spolu s žáky 2. ročníku rozlišovat sudá a lichá čísla.parita sudého čísla je nula, parita lichého čísla je jedna). Lichá = 2Z + 1 = { …, −3, −1, 1, 3, 5, … } Je vidět, že libovolné sudé číslo je možno vyjádřit ve tvaru 2k, kde k ∈ Z, zatímco libovolné liché číslo je možno vyjádřit jako 2k + 1, opět pro k ∈ Z.
Jak se pozná liché číslo : Lichá čísla jsou celá čísla, která po dělení dvěma dávají zbytek jedna. Lichá čísla končí cifrou 1, 3, 5, 7 nebo 9. Příklady lichých čísel jsou 15, 891, -7, 1, 95.
Kolik je přirozených čísel od 1 do 100
Součet přirozených čísel od 1 do 100 je 5 050.
Jak zjistím jestli je funkce sudá nebo lichá : Funkce sudá a lichá
Sudou, anebo lichou funkci poznáme snadno z grafu funkce. Jestliže je graf osově souměrný podle osy y, pak se jedná o funkci sudou. V případě, že je graf funkce středově souměrný podle počátku soustavy souřadnic, pak se jedná o funkci lichou. f(x)=f(-x).
Číslo je abstraktní entita užívaná pro vyjádření množství nebo pořadí. Přirozeným číslem se v matematice rozumí číslo, které je možné použít pro vyjádření počtu („na stole je šest mincí“) nebo pořadí („toto je třetí největší město“) prvků konečných množin.
Jak poznat celá čísla
Celá čísla jsou čísla přirozená, čísla k nim opačná a číslo nula. Obor celých čísel značíme Z. Zapisujeme: Z = {…,-3, -2, -1, 0, 1, 2, 3,…}Přirozeným číslem se v matematice rozumí číslo, které je možné použít pro vyjádření počtu („na stole je šest mincí“) nebo pořadí („toto je třetí největší město“) prvků konečných množin.Googol je přibližný počet atomů vodíku v rámci nám známého vesmíru. V roce 1938 vymyslel Milton Sirotta, devítiletý synovec slavného amerického matematika Edwarda Kasnera, pojem „googol“ označující číslo 10100, tedy jedničku se sto nulami. Sudá čísla končí cifrou 0, 2, 4, 6 nebo 8. Příklady sudých čísel jsou 138, 12, 0, 9356, -34, 6. Lichá čísla jsou celá čísla, která po dělení dvěma dávají zbytek jedna. Lichá čísla končí cifrou 1, 3, 5, 7 nebo 9.
Jak poznat jestli se jedná o funkci : U lineární funkce, když máme nějakou změnu x, která je stejná, když se nám x mění o nějakou stejnou hodnotu, tak se nám i y musí měnit o stejnou hodnotu, ta změna musí být konstantní. Pokud se při změně x mění y o stále stejnou hodnotu, pak se jedná o lineární funkci.
Jak zjistit co je to za číslo : Jak zjistit majitele telefonního čísla
Zavolejte na něj. Buď se přímo zeptejte, nebo – když vám to stojí za to – můžete předstírat omyl.
Vyzkoušejte služby pro identifikaci. Je jich celá řada: kdomivolal.eu, kdovolal.cz, kdovolal.eu, muzutozvednout.cz, vyhledatcislo.cz, telefonniseznam.org.
Zkuste Google.
Kdo mi volal co je to za číslo
Některé internetové stránky obsahují databázi telefonních čísel, pod kterými návštěvníci v diskusních fórech spekulují, komu asi daný kontakt patří. Takže jestli vám nepomohly předchozí rady, zajděte na adresu kdomivolal.eu, kdovolal.cz, kdovolal.eu, muzutozvednout.cz, nevolejte.cz, pozadavek.cz anebo vyhledatcislo.cz. Pravidla dělitelnosti
Číslo je dělitelné dvěmi, jestliže je sudé.
Číslo je dělitelné třemi, jestliže ciferný součet je dělitelný třemi.
Číslo je dělitelné čtyřmi, jestliže je poslední dvojčíslí dělitelné čtyřmi.
Číslo je dělitelné pěti, jestliže končí nulou nebo pětkou.
Nula se používá ve dvou funkcích: Číslo nula ve významu matematického prázdna, prostého nic. Číslo 0 na číselné ose odděluje záporná čísla od kladných. V teorii množin je nula velikost (kardinalita) prázdné množiny.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jaké jsou lichá čísla? Weitere Antworten – Kolik je Lichych čísel do 100
1+99=3+97=5+95=100. Obecně se dá říci, že ve dvojici jsou čísla k a 100−k, takže jejich součet je opravdu 100. Lichých čísel je polovina ze všech celých čísel od 1 do 100, tedy 50, a z nich vytvoříme 25 dvojic, každou se součtem 100. Celkový součet všech kladných lichých čísel menších než 100 je tedy 2500.Když děti učí telka! Naučme se spolu s žáky 2. ročníku rozlišovat sudá a lichá čísla.parita sudého čísla je nula, parita lichého čísla je jedna). Lichá = 2Z + 1 = { …, −3, −1, 1, 3, 5, … } Je vidět, že libovolné sudé číslo je možno vyjádřit ve tvaru 2k, kde k ∈ Z, zatímco libovolné liché číslo je možno vyjádřit jako 2k + 1, opět pro k ∈ Z.
Jak se pozná liché číslo : Lichá čísla jsou celá čísla, která po dělení dvěma dávají zbytek jedna. Lichá čísla končí cifrou 1, 3, 5, 7 nebo 9. Příklady lichých čísel jsou 15, 891, -7, 1, 95.
Kolik je přirozených čísel od 1 do 100
Součet přirozených čísel od 1 do 100 je 5 050.
Jak zjistím jestli je funkce sudá nebo lichá : Funkce sudá a lichá
Sudou, anebo lichou funkci poznáme snadno z grafu funkce. Jestliže je graf osově souměrný podle osy y, pak se jedná o funkci sudou. V případě, že je graf funkce středově souměrný podle počátku soustavy souřadnic, pak se jedná o funkci lichou. f(x)=f(-x).
Číslo je abstraktní entita užívaná pro vyjádření množství nebo pořadí.
Přirozeným číslem se v matematice rozumí číslo, které je možné použít pro vyjádření počtu („na stole je šest mincí“) nebo pořadí („toto je třetí největší město“) prvků konečných množin.
Jak poznat celá čísla
Celá čísla jsou čísla přirozená, čísla k nim opačná a číslo nula. Obor celých čísel značíme Z. Zapisujeme: Z = {…,-3, -2, -1, 0, 1, 2, 3,…}Přirozeným číslem se v matematice rozumí číslo, které je možné použít pro vyjádření počtu („na stole je šest mincí“) nebo pořadí („toto je třetí největší město“) prvků konečných množin.Googol je přibližný počet atomů vodíku v rámci nám známého vesmíru. V roce 1938 vymyslel Milton Sirotta, devítiletý synovec slavného amerického matematika Edwarda Kasnera, pojem „googol“ označující číslo 10100, tedy jedničku se sto nulami.
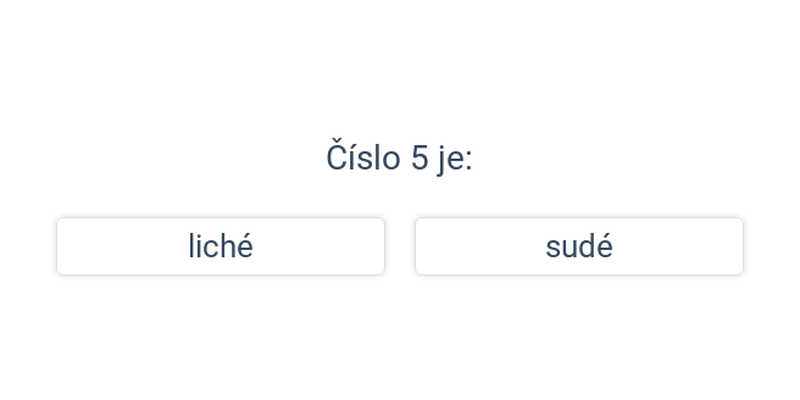
Sudá čísla končí cifrou 0, 2, 4, 6 nebo 8. Příklady sudých čísel jsou 138, 12, 0, 9356, -34, 6. Lichá čísla jsou celá čísla, která po dělení dvěma dávají zbytek jedna. Lichá čísla končí cifrou 1, 3, 5, 7 nebo 9.
Jak poznat jestli se jedná o funkci : U lineární funkce, když máme nějakou změnu x, která je stejná, když se nám x mění o nějakou stejnou hodnotu, tak se nám i y musí měnit o stejnou hodnotu, ta změna musí být konstantní. Pokud se při změně x mění y o stále stejnou hodnotu, pak se jedná o lineární funkci.
Jak zjistit co je to za číslo : Jak zjistit majitele telefonního čísla
Kdo mi volal co je to za číslo
Některé internetové stránky obsahují databázi telefonních čísel, pod kterými návštěvníci v diskusních fórech spekulují, komu asi daný kontakt patří. Takže jestli vám nepomohly předchozí rady, zajděte na adresu kdomivolal.eu, kdovolal.cz, kdovolal.eu, muzutozvednout.cz, nevolejte.cz, pozadavek.cz anebo vyhledatcislo.cz.
Pravidla dělitelnosti
Nula se používá ve dvou funkcích: Číslo nula ve významu matematického prázdna, prostého nic. Číslo 0 na číselné ose odděluje záporná čísla od kladných. V teorii množin je nula velikost (kardinalita) prázdné množiny.
Jaké máme druhy čísel : 1.1 Číselné obory