Obvod kruhu (i kružnice) o poloměru r je o = 2 π r o=2\pi r o=2πr. Pro průměr d platí o = π d o = \pi d o=πd. Konstanta π se nazývá též Ludolfovo číslo. π je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě.Obvod je součet délek čar, které útvar vymezují. Obvod se měří v jednotkách délky.Obsah kruhu je pí krát poloměr na druhou (S = π r²). V továrně vyrábí čokoládové sušenky kruhového tvaru. Průměr sušenky je 16 milimetrů.
Kolik pi je kruh : π = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510…
Jaký je vzorec pro obvod obdélníku
obvod obdélníku = 2 * (a + b)
U trojúhelníků musíte sečíst délku všech tří jeho stran. Právě tak získáte celkový obvod trojúhelníku.
Jaký je vzorec pro obvod trojúhelníku : Obvod trojúhelníku je součtem délek jeho tří stran.
Dejme tomu, že například potřebujeme v tabulce vypočítat obvod kruhu o poloměru 3 cm. Vzorec pro výpočet pak bude mít tvar =2*PI()*buňka s hodnotou poloměru. Jak již bylo řečeno v úvodu, funkce PI() generuje hodnotu Ludolfova čísla s přesností na 15 desetinných míst. Obsah vyjadřuje, kolik „místa v rovině“ útvar zaujímá. Měří se v jednotkách obsahu. Obvod značíme o. Obvod je součet délek čar, které útvar vymezují.
Jaký je vzorec pro obsah obdélníku
Abychom zjistili obsah obdélníku, musíme vynásobit délku obdélníku s šířkou obdélníku.Průměr kružnice je úsečka, která prochází středem kružnice a jejíž oba krajní body leží na této kružnici.A to že 2 pí radiánů je 360 stupňů. V dalším videu si ukážem několik příkladů, abychom se ujistili, že umíme převádět oběma směry. Tato konstanta je jedním z nejdůležitějších čísel vůbec – a současně bylo vždy v dějinách tak trošku záhadou. Zpočátku se Den pí slavil jen v USA v úzké komunitě vědců. Čtrnáctý březen byl vybrán proto, že Američané píšou datum obráceně, čtrnáctý březen tedy zapisují jako 3.14 – což jsou první čísla pí.
Jak vypočítat obvod kružnice opsané : Obvod kružnice se spočítá jako 3,14 [π] x průměr kružnice [d], nebo 2 x 3,14 [π] x poloměr kružnice [r].
Co je délka obdélníku : Délka obdélníku je , jeho šířka je o kratší než délka.
Co je to Těžnice v trojúhelníku
Těžnice je úsečka spojující vrchol trojúhelníku se středem jeho protější stany. Příkladem v ABC je težnice ta, která je úsečkou ASa. Obdobně tak existují těžnice ke stranám b, c. Každý trojúhelník má tedy tři těžnice. Obvod výseče
Obvod celé výseče je roven součtu délky kruhového oblouku a dvojnásobku poloměru, tedy. , kde úhel θ je zadán v radiánech.Jelikož má čtverec všechny strany stejně dlouhé, stačí nám pro výpočet jeho obsahu znalost délky jedné jeho strany. Pro výpočet obsahu čtverce tedy do kalkulačky zadejte délku strany čtverce a. Obsah čtverce se spočítá jako délka strany [a] x délka strany [a].
Jak se měří obsah : Obsah je fyzikální veličina, která vyjadřuje plochu nějakého geometrického tvaru. Obsah se zpravidla měří v čtverečných jednotkách, například čtverečných metrech (m²) nebo čtverečných centimetrech (cm²). Kde π (pi) je matematická konstanta přibližně rovna 3,14159.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jaký je vzorec pro výpočet obvodu kruhu? Weitere Antworten – Jaký je vzorec pro Obvod kruhu
Obvod kruhu (i kružnice) o poloměru r je o = 2 π r o=2\pi r o=2πr. Pro průměr d platí o = π d o = \pi d o=πd. Konstanta π se nazývá též Ludolfovo číslo. π je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě.Obvod je součet délek čar, které útvar vymezují. Obvod se měří v jednotkách délky.Obsah kruhu je pí krát poloměr na druhou (S = π r²). V továrně vyrábí čokoládové sušenky kruhového tvaru. Průměr sušenky je 16 milimetrů.
Kolik pi je kruh : π = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510…
Jaký je vzorec pro obvod obdélníku
obvod obdélníku = 2 * (a + b)
U trojúhelníků musíte sečíst délku všech tří jeho stran. Právě tak získáte celkový obvod trojúhelníku.
Jaký je vzorec pro obvod trojúhelníku : Obvod trojúhelníku je součtem délek jeho tří stran.
Dejme tomu, že například potřebujeme v tabulce vypočítat obvod kruhu o poloměru 3 cm. Vzorec pro výpočet pak bude mít tvar =2*PI()*buňka s hodnotou poloměru. Jak již bylo řečeno v úvodu, funkce PI() generuje hodnotu Ludolfova čísla s přesností na 15 desetinných míst.
Obsah vyjadřuje, kolik „místa v rovině“ útvar zaujímá. Měří se v jednotkách obsahu. Obvod značíme o. Obvod je součet délek čar, které útvar vymezují.
Jaký je vzorec pro obsah obdélníku
Abychom zjistili obsah obdélníku, musíme vynásobit délku obdélníku s šířkou obdélníku.Průměr kružnice je úsečka, která prochází středem kružnice a jejíž oba krajní body leží na této kružnici.A to že 2 pí radiánů je 360 stupňů. V dalším videu si ukážem několik příkladů, abychom se ujistili, že umíme převádět oběma směry.
Tato konstanta je jedním z nejdůležitějších čísel vůbec – a současně bylo vždy v dějinách tak trošku záhadou. Zpočátku se Den pí slavil jen v USA v úzké komunitě vědců. Čtrnáctý březen byl vybrán proto, že Američané píšou datum obráceně, čtrnáctý březen tedy zapisují jako 3.14 – což jsou první čísla pí.
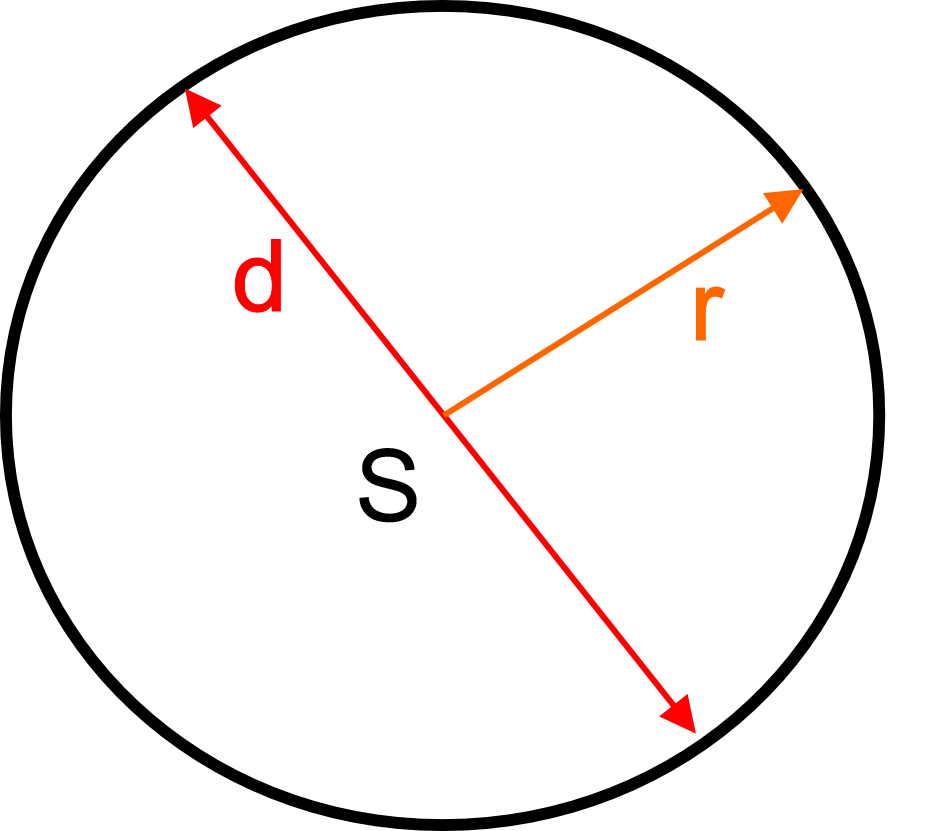
Jak vypočítat obvod kružnice opsané : Obvod kružnice se spočítá jako 3,14 [π] x průměr kružnice [d], nebo 2 x 3,14 [π] x poloměr kružnice [r].
Co je délka obdélníku : Délka obdélníku je , jeho šířka je o kratší než délka.
Co je to Těžnice v trojúhelníku
Těžnice je úsečka spojující vrchol trojúhelníku se středem jeho protější stany. Příkladem v ABC je težnice ta, která je úsečkou ASa. Obdobně tak existují těžnice ke stranám b, c. Každý trojúhelník má tedy tři těžnice.
Obvod výseče
Obvod celé výseče je roven součtu délky kruhového oblouku a dvojnásobku poloměru, tedy. , kde úhel θ je zadán v radiánech.Jelikož má čtverec všechny strany stejně dlouhé, stačí nám pro výpočet jeho obsahu znalost délky jedné jeho strany. Pro výpočet obsahu čtverce tedy do kalkulačky zadejte délku strany čtverce a. Obsah čtverce se spočítá jako délka strany [a] x délka strany [a].
Jak se měří obsah : Obsah je fyzikální veličina, která vyjadřuje plochu nějakého geometrického tvaru. Obsah se zpravidla měří v čtverečných jednotkách, například čtverečných metrech (m²) nebo čtverečných centimetrech (cm²). Kde π (pi) je matematická konstanta přibližně rovna 3,14159.