Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku. Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
Jak se vypočítá trojúhelník : Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.
Jak vypočítat jednu stranu trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak vypočítat poměr stran trojúhelníku : Při rozdělení v daném poměru musíme sečíst všechny členy poměru ( počet dílů) a ze známého celku vypočítat velikost jednoho dílu. Cv20/7 V trojúhelníku jsou délky stran v postupném poměru 5 : 7 : 9, nejdelší strana má 27 cm.
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 . Pythagorova věta
c2 = a2 + b2 – tedy:
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených nad jeho odvěsnami.
Co je to Odvesna
Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Zjištění poměru stran
Vypočítejte vztah mezi šířkou (první číslo) a výškou (druhé číslo). Například: Obrázky s rozměry 1 600 x 900 pixelů nebo 3 200 x 1 800 pixelů mají poměr stran 16:9. Obrázky s rozměry 1 600 x 1 600 pixelů a 3 200 x 3 200 pixelů mají poměr stran 1:1. Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.
Jak zjistit Odvěsnu : V pravoúhlém trojúhelníku je přepona nejdelší stranou. "Protilehlá odvěsna" je strana naproti zadanému úhlu a "přilehlá odvěsna" je strana vedle daného úhlu.
Jak se vypočítá poměr : Kolik je ve třídě dívek a kolik chlapců (Pozn.: Poměr chlapci : dívky je pak 2 : 3.) Ve třídě je tedy 18 dívek a 12 chlapců. Dohromady tedy 30 lidí. Obecný postup je tedy takový, že sečteme čísla v poměru, tímto součtem vydělíme celkový počet lidí ve třídě a získaným číslem vynásobíme jednotlivá čísla v poměru.
Jak dopočítat stranu
Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 . ↑ ander: obsah čtverce získáš tak že umocníš délku jeho strany na druhou. Obráceně tedy získáš délku strany tak že obsah čtverce omocníš. Dva jsou tisíckrát jeden.Zjištění poměru stran
Vypočítejte vztah mezi šířkou (první číslo) a výškou (druhé číslo). Například: Obrázky s rozměry 1 600 x 900 pixelů nebo 3 200 x 1 800 pixelů mají poměr stran 16:9. Obrázky s rozměry 1 600 x 1 600 pixelů a 3 200 x 3 200 pixelů mají poměr stran 1:1.
Jak vyjadrit poměr : Čísla a, b můžeme porovnat rozdílem: a – b (například 18 – 6→ 18 je o 12 větší než 6) Čísla a, b můžeme porovnat podílem: a : b (například 18 : 6→ 18 je 3krát větší než 6) Tomuto podílu a : b říkáme poměr. Čteme: a ku b Poměr dvou čísel je naznačené dělení (zlomek).
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Jak dopočítat stranu trojúhelníku? Weitere Antworten – Jak Vypocitat stranu BV trojúhelníku
Vysvětlíme si, jak lze vypočítat délku strany trojúhelníku při zadaném obsahu a délce dvou dalších stran. Pro výpočet použijeme vzorec pro obsah trojúhelníku (strana krát výška)/2.Pythagoras byl také zakladatelem pythagorejské školy, která se věnovala studiu matematických a filosofických otázek. Vztah Pythagorovy věty lze vyjádřit jako c² = a² + b². Tento vzorec říká, že obsah čtverce sestrojeného na přeponě pravoúhlého trojúhelníku je roven součtu obsahů čtverců sestrojených na jeho odvěsnách.Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku. Věta zní: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
Jak se vypočítá trojúhelník : Pro výpočet obsahu trojúhelníku použijeme vzorec obsah = (strana krá výška)/2.
Jak vypočítat jednu stranu trojúhelníku
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Jak vypočítat poměr stran trojúhelníku : Při rozdělení v daném poměru musíme sečíst všechny členy poměru ( počet dílů) a ze známého celku vypočítat velikost jednoho dílu. Cv20/7 V trojúhelníku jsou délky stran v postupném poměru 5 : 7 : 9, nejdelší strana má 27 cm.
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
Pythagorova věta
Co je to Odvesna
Nejdelší strana v pravoúhlém trojúhelníku se nazývá přepona. Přepona leží proti pravému úhlu. Zbývající dvě strany nazýváme odvěsny.Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .Zjištění poměru stran
Vypočítejte vztah mezi šířkou (první číslo) a výškou (druhé číslo). Například: Obrázky s rozměry 1 600 x 900 pixelů nebo 3 200 x 1 800 pixelů mají poměr stran 16:9. Obrázky s rozměry 1 600 x 1 600 pixelů a 3 200 x 3 200 pixelů mají poměr stran 1:1.
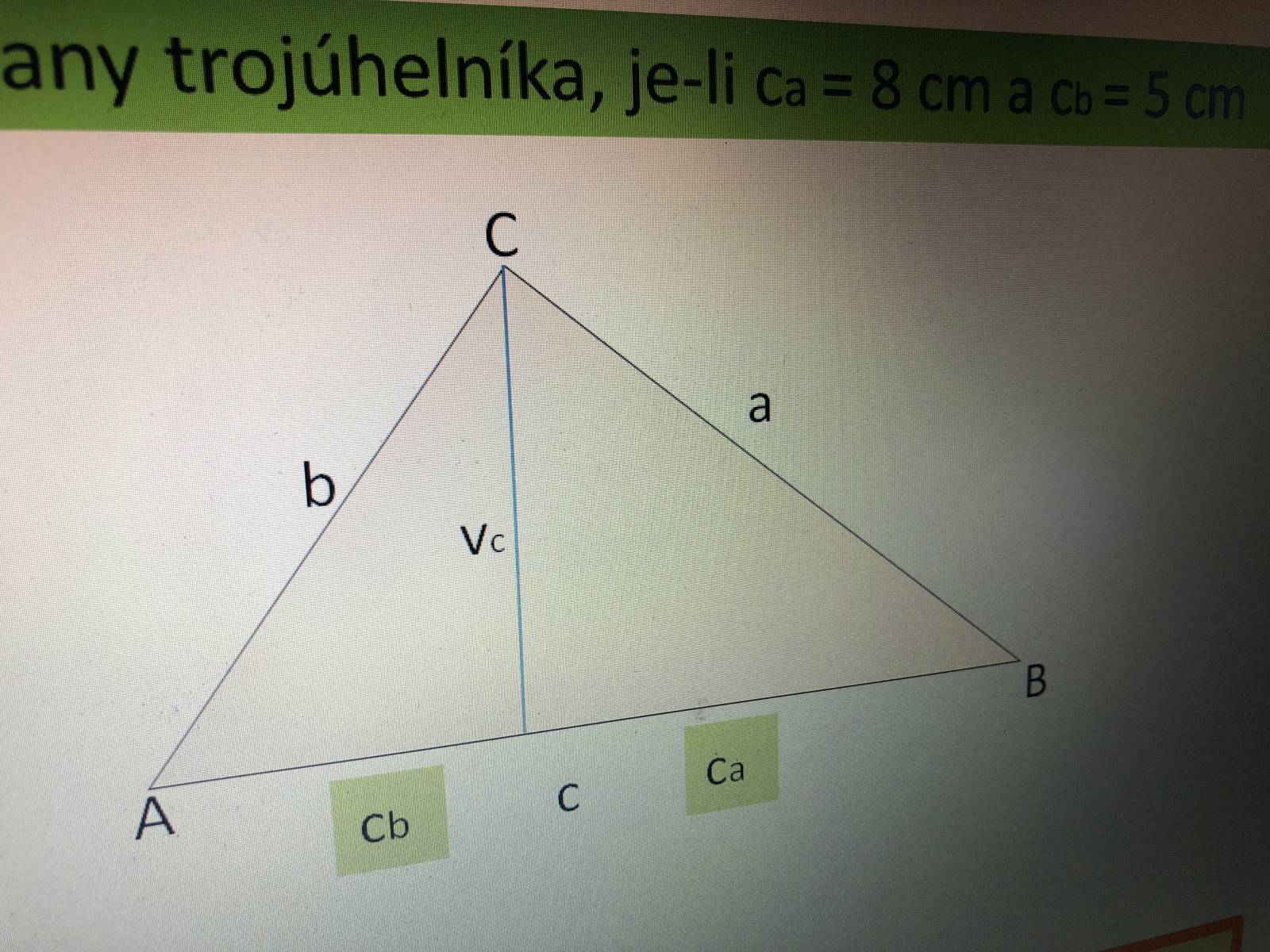
Trojúhelníky hrají v geometrii klíčovou roli, protože mnoho problémů lze řešit tak, že složitější obrazce rozdělíme na trojúhelníky a následně pracujeme s nimi. Značení stran a úhlů v trojúhelníku: Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.
Jak zjistit Odvěsnu : V pravoúhlém trojúhelníku je přepona nejdelší stranou. "Protilehlá odvěsna" je strana naproti zadanému úhlu a "přilehlá odvěsna" je strana vedle daného úhlu.
Jak se vypočítá poměr : Kolik je ve třídě dívek a kolik chlapců (Pozn.: Poměr chlapci : dívky je pak 2 : 3.) Ve třídě je tedy 18 dívek a 12 chlapců. Dohromady tedy 30 lidí. Obecný postup je tedy takový, že sečteme čísla v poměru, tímto součtem vydělíme celkový počet lidí ve třídě a získaným číslem vynásobíme jednotlivá čísla v poměru.
Jak dopočítat stranu
Pythagorova věta: základní použití
Pythagorova věta umožňuje dopočítat délku třetí strany pravoúhlého trojúhelníka, u kterého známe délky dvou zbývajících stran: Délka přepony c = a 2 + b 2 c = \sqrt{a^2 + b^2} c=a2+b2 .
↑ ander: obsah čtverce získáš tak že umocníš délku jeho strany na druhou. Obráceně tedy získáš délku strany tak že obsah čtverce omocníš. Dva jsou tisíckrát jeden.Zjištění poměru stran
Vypočítejte vztah mezi šířkou (první číslo) a výškou (druhé číslo). Například: Obrázky s rozměry 1 600 x 900 pixelů nebo 3 200 x 1 800 pixelů mají poměr stran 16:9. Obrázky s rozměry 1 600 x 1 600 pixelů a 3 200 x 3 200 pixelů mají poměr stran 1:1.
Jak vyjadrit poměr : Čísla a, b můžeme porovnat rozdílem: a – b (například 18 – 6→ 18 je o 12 větší než 6) Čísla a, b můžeme porovnat podílem: a : b (například 18 : 6→ 18 je 3krát větší než 6) Tomuto podílu a : b říkáme poměr. Čteme: a ku b Poměr dvou čísel je naznačené dělení (zlomek).