Antwort How do you solve a 1 in a matrix? Weitere Antworten – What does a-1 mean in matrix

How do you solve a 1 in a matrix?
If we consider a matrix A, we denote its inverse as A-1. The inverse of a matrix is another matrix that, when multiplied by the given matrix, yields the multiplicative identity. For a matrix A, its inverse is A-1. And A.A-1 = I, where I is denoted as the identity matrix.For a 2×2 matrix, the inverse is: (abcd)−1=1ad−bc(d−b−ca) , where ad−bc≠0. just swap the 'a' and 'd', negate the 'b' and 'c', then divide all by the determinant ad−bc. That's really the most straightforward 'trick', just memorize that pattern.Only square matrices have inverses, so if it's not square, it doesn't have one. If it is square, check if its determinant is 0. If it's not 0, it has an inverse, if it is 0, it doesn't. You can also check if any of the rows and/or columns are linearly dependent.

Does every matrix have an inverse : Not all 2 × 2 matrices have an inverse matrix. If the determinant of the matrix is zero, then it will not have an inverse; the matrix is then said to be singular. Only non-singular matrices have inverses.

How to find a 1 in matrix

A-1= adj(A)/det(A),

take the transpose of a cofactor matrix. Here, Mij refers to the (i,j)th minor matrix after removing the ith row and the jth column. You can also say that the transpose of a cofactor matrix is also called the adjoint of a matrix A. Learn how to find the adjoint of a matrix here.

What is matrix A * A 1 : The inverse of a square matrix A, denoted by A-1, is the matrix so that the product of A and A-1 is the identity matrix. The identity matrix that results will be the same size as matrix A.

A-1= adj(A)/det(A),

To find the Inverse of a 3 × 3 Matrix A, you can use the formula A-1 = (adj A) / (det A), where: adj A is the adjoint matrix of A.

How to find a-1 of a 2×2 matrix

Now d is still 5 negative b that's going to be negative 2 negative c is negative 17. And a is 7. Seven times five is thirty five. Two times seventeen is thirty four.1/1

“ The inverse of x is equal to 1/x. So, the inverse of 1 is equal to 1/1, which is 1.Now d is still 5 negative b that's going to be negative 2 negative c is negative 17. And a is 7. Seven times five is thirty five. Two times seventeen is thirty four.

In mathematics, a matrix of ones or all-ones matrix is a matrix where every entry is equal to one. Examples of standard notation are given below: Some sources call the all-ones matrix the unit matrix, but that term may also refer to the identity matrix, a different type of matrix.

Is a 1 invertible : However, if A is symmetric it is true (Hermitian in the complex case): Let A have eigenvalues ai, and note that A+A−1 has eigenvalues ai+a−1i. These are zero if and only if a2i=−1. But this is not possible since ai is real. Hence A+A−1 is invertible.

What is the inverse of a 2×2 matrix : What is the Inverse of 2×2 Matrix The inverse of a 2×2 matrix, say A, is a matrix of the same order denoted by A-1 such that AA-1 = A-1A = I, where I is the identity matrix of order 2×2. i.e., I = ⎡⎢⎣1001⎤⎥⎦ [ 1 0 0 1 ] .

What is inverse transform of 1

what is the inverse laplace of 1 The inverse laplace of 1 is the dirac delta function d(t). The inverse laplace transform of any number (K) is K*d(t).

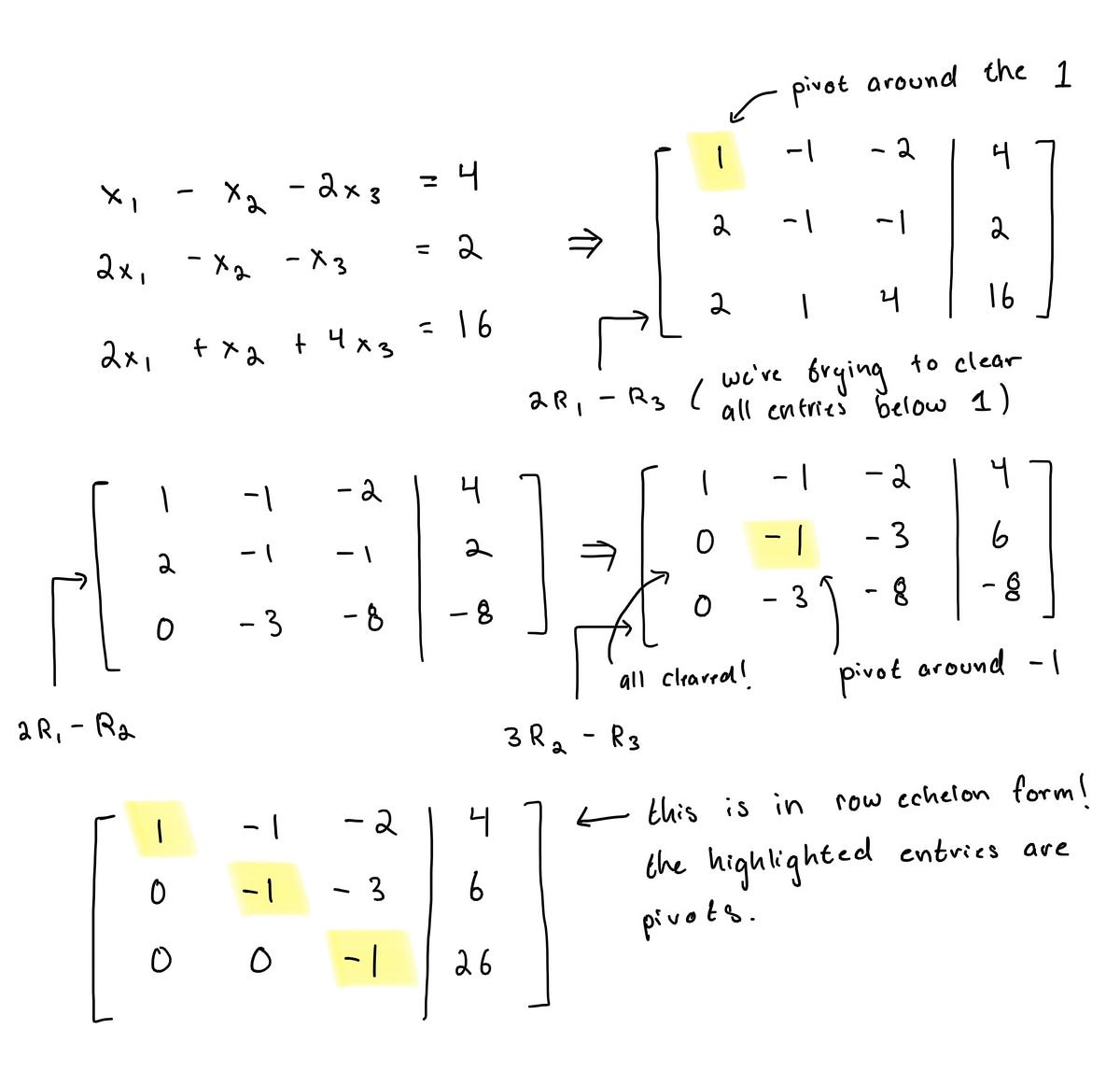
In mathematics, −1 (negative one or minus one) is the additive inverse of 1, that is, the number that when added to 1 gives the additive identity element, 0. It is the negative integer greater than negative two (−2) and less than 0.Since a zero determinant of any n x n matrix implies that the rank must be less than n, the rank for a 2×2 matrix must be 0 (null matrix) or 1. As a standard exercise in linear algebra, we can show that any rank-1 matrix may be written as the outer product of two vectors, a well-documented result in textbooks.