Dvě úsečky jsou shodné, když mají stejnou délku. Př. 2: Kdy jsou shodné dva úhly Dva úhly jsou shodné, když mají stejnou velikost.Dvě přímky p(P, u) a q(Q, v) jsou totožné právě tehdy, jsou-li rovnoběžné a leží-li bod Q na přímce p. Jsou-li přímky p(P, u) a q(Q, v) totožné, pak jsou rovnoběžné (u je násobkem v) a bod Q leží na přímce p.Úsečka – je část přímky, ohraničená dvěma krajními body. Úsečku označujeme krajními body, takže můžeme mluvit o úsečce AB, pokud má krajní body A a B.
Jak se zapisuje shodnost : Stručně se označují sss, sus, usu, Ssu, přičemž věta sss je vlastně definicí 1.3.
Co to je shodná úsečka
Shodnost úseček je vztah mezi úsečkami, který je v geometrii zaveden pomocí axiomů shodnosti. Je to relace reflexivní, symetrická a tranzitivní na množině všech úseček v prostoru, tedy ekvivalence, která rozkládá množinu všech úseček na třídy navzájem shodných úseček.
Co patří do shodných zobrazení : Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost.
Shodnost úseček je vztah mezi úsečkami, který je v geometrii zaveden pomocí axiomů shodnosti. Je to relace reflexivní, symetrická a tranzitivní na množině všech úseček v prostoru, tedy ekvivalence, která rozkládá množinu všech úseček na třídy navzájem shodných úseček. sss, sus, uu Označení věty zkratkou vyjadřuje, kterými údaji trojúhelníky porovnáváme. VĚTA sss Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících si stran, jsou podobné.
Kdy jsou úsečky shodné
Shodné úsečky mají stejnou délku.Osa úsečky je přímka kolmá k úsečce procházející jejím středem. Všechny body na ose úsečky mají od obou krajních bodů stejnou vzdálenost. Úsečka je středově souměrná podle svého středu.Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné. Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení. Je-li poměr podobnosti k ˂ 1, jedná se o zmenšení.
Co je to přímá a nepřímá shodnost : Přímá a nepřímá shodnost
Shodnost zachovávající orientaci se nazývá přímá neboli přemístění. Shodnost měnící orientaci se nazývá nepřímá. Posunutí a otočení (a tedy i středová souměrnost) jsou přímé shodnosti (přemístění), zachovávají orientaci. (Posunuté) osové souměrnosti jsou nepřímé shodnosti, mění orientaci.
Co je to shodné zobrazení : Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost. Z definice shodného zobrazení plyne, že každé shodné zobrazení je prosté.
Co jsou to shodné útvary
Jestliže dva rovinné útvary můžeme přemístit tak, že se kryjí,budeme je nazývat shodnými útvary. Jestliže se dva trojúhelníky shodují ve všech třech stranách, pak jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.VĚTA sus Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.
Jak je na základě shodnosti úseček definován střed úsečky : Střed úsečky můžeme dále určovat odhadem pomocí kružítka: Sestrojíme oblouky dvou shodných kružnic se středy v krajních bodech úsečky AB a poloměrem přibližně poloviny úsečky AB. Střed úsečky pak snadno odhadneme jako střed úsečky, jejíž krajní body jsou průsečíky obou oblouků s úsečkou AB.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Co to jsou shodné úsečky? Weitere Antworten – Kdy jsou shodné dvě úsečky
Dvě úsečky jsou shodné, když mají stejnou délku. Př. 2: Kdy jsou shodné dva úhly Dva úhly jsou shodné, když mají stejnou velikost.Dvě přímky p(P, u) a q(Q, v) jsou totožné právě tehdy, jsou-li rovnoběžné a leží-li bod Q na přímce p. Jsou-li přímky p(P, u) a q(Q, v) totožné, pak jsou rovnoběžné (u je násobkem v) a bod Q leží na přímce p.Úsečka – je část přímky, ohraničená dvěma krajními body. Úsečku označujeme krajními body, takže můžeme mluvit o úsečce AB, pokud má krajní body A a B.
Jak se zapisuje shodnost : Stručně se označují sss, sus, usu, Ssu, přičemž věta sss je vlastně definicí 1.3.
Co to je shodná úsečka
Shodnost úseček je vztah mezi úsečkami, který je v geometrii zaveden pomocí axiomů shodnosti. Je to relace reflexivní, symetrická a tranzitivní na množině všech úseček v prostoru, tedy ekvivalence, která rozkládá množinu všech úseček na třídy navzájem shodných úseček.
Co patří do shodných zobrazení : Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost.
Shodnost úseček je vztah mezi úsečkami, který je v geometrii zaveden pomocí axiomů shodnosti. Je to relace reflexivní, symetrická a tranzitivní na množině všech úseček v prostoru, tedy ekvivalence, která rozkládá množinu všech úseček na třídy navzájem shodných úseček.
sss, sus, uu Označení věty zkratkou vyjadřuje, kterými údaji trojúhelníky porovnáváme. VĚTA sss Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících si stran, jsou podobné.
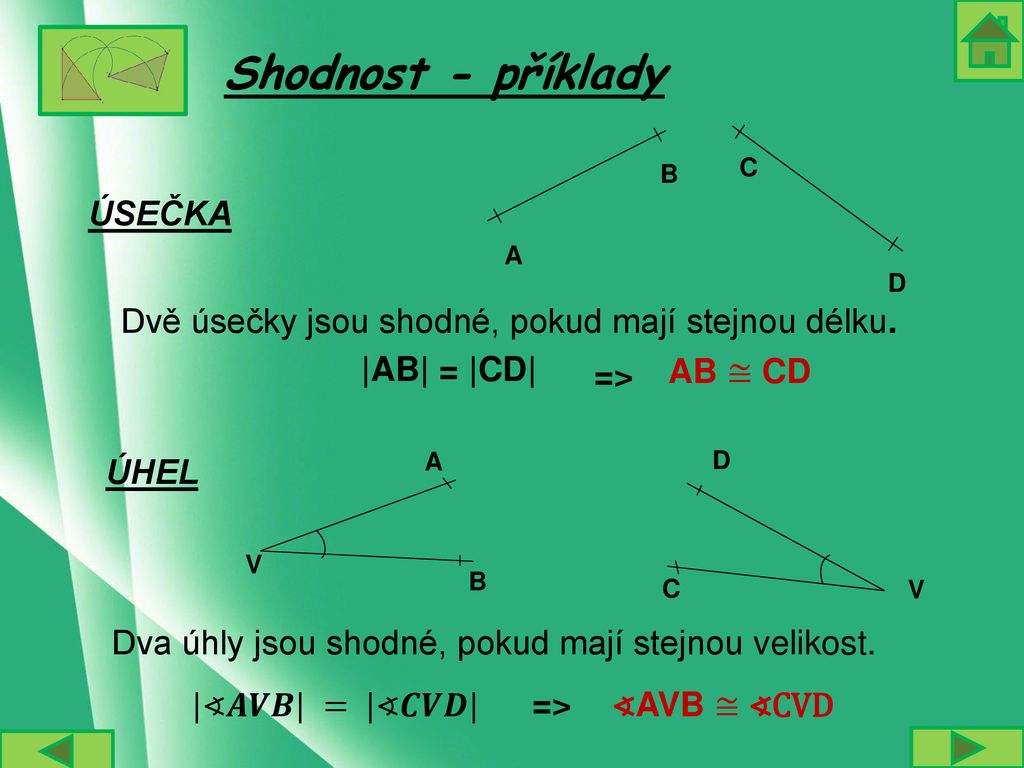
Kdy jsou úsečky shodné
Shodné úsečky mají stejnou délku.Osa úsečky je přímka kolmá k úsečce procházející jejím středem. Všechny body na ose úsečky mají od obou krajních bodů stejnou vzdálenost. Úsečka je středově souměrná podle svého středu.Věta sss: Dva trojúhelníky, které se shodují ve všech třech stranách, jsou shodné. Věta usu: Dva trojúhelníky, které se shodují v jedné straně a úhlech přilehlých k této straně, jsou shodné. Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.
Jestliže se dva trojúhelníky shodují ve dvou vnitřních úhlech, pak jsou podobné. Jestliže dva trojúhelníky mají stejný poměr délek dvou párů odpovídajících si stran a shodují se v úhlu jimi sevřeném, pak jsou podobné. Je-li poměr podobnosti k ˃ 1, jedná se o zvětšení. Je-li poměr podobnosti k ˂ 1, jedná se o zmenšení.
Co je to přímá a nepřímá shodnost : Přímá a nepřímá shodnost
Shodnost zachovávající orientaci se nazývá přímá neboli přemístění. Shodnost měnící orientaci se nazývá nepřímá. Posunutí a otočení (a tedy i středová souměrnost) jsou přímé shodnosti (přemístění), zachovávají orientaci. (Posunuté) osové souměrnosti jsou nepřímé shodnosti, mění orientaci.
Co je to shodné zobrazení : Shodná zobrazení Zobrazení f v rovině je shodné zobrazení, jestliže pro každé dva body X, Y roviny a jejich obrazy X', Y' platí |XY|=|X'Y'|. Shodné zobrazení v rovině se rovněž nazývá shodnost. Z definice shodného zobrazení plyne, že každé shodné zobrazení je prosté.
Co jsou to shodné útvary
Jestliže dva rovinné útvary můžeme přemístit tak, že se kryjí,budeme je nazývat shodnými útvary. Jestliže se dva trojúhelníky shodují ve všech třech stranách, pak jsou shodné.
Věta sus: Dva trojúhelníky, které se shodují ve dvou stranách a úhlu jimi sevřeném, jsou shodné.VĚTA sus Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících si stran a shodují se v úhlu jimi sevřeném, jsou podobné.
Jak je na základě shodnosti úseček definován střed úsečky : Střed úsečky můžeme dále určovat odhadem pomocí kružítka: Sestrojíme oblouky dvou shodných kružnic se středy v krajních bodech úsečky AB a poloměrem přibližně poloviny úsečky AB. Střed úsečky pak snadno odhadneme jako střed úsečky, jejíž krajní body jsou průsečíky obou oblouků s úsečkou AB.