Antwort Co je to sjednocení množin? Weitere Antworten – Jak se dělá sjednocení množin

Co je to sjednocení množin?
Sjednocení množin

Ukázkový příklad: Mějme dvě množiny A = {1, 3, 5, 7} a B = {2, 4, 6}. Sjednocením vznikne množina: A ∪ B = {1, 2, 3, 4, 5, 6, 7}. Výsledná množina obsahuje prvky obou množin.V matematice se jako průnik dvou nebo více množin označuje taková množina, která obsahuje pouze ty prvky, které se nalézají ve všech těchto množinách. Průnik množin A a B se označuje symbolem A ∩ B.Mějme dvě množiny A a B, kde navíc platí B \subseteq A. V takové situaci zavádíme pojem doplněk množiny. Je-li B \subseteq A, pak doplňkem množiny B vzhledem k množině A je množina, která obsahuje všechny prvky z A, které zároveň nejsou v B.

Co znamená sjednocení : http://www.mathematicator.com Máme dvě množiny s konečným počtem prvků. Průnik těchto dvou množin uděláme tak, že vybereme prvky, které mají obě množiny společné. Naopak sjednocení vznikne tak, že vybereme prvky, které jsou zastoupeny alespoň v jedné z množin.

Co je ∩

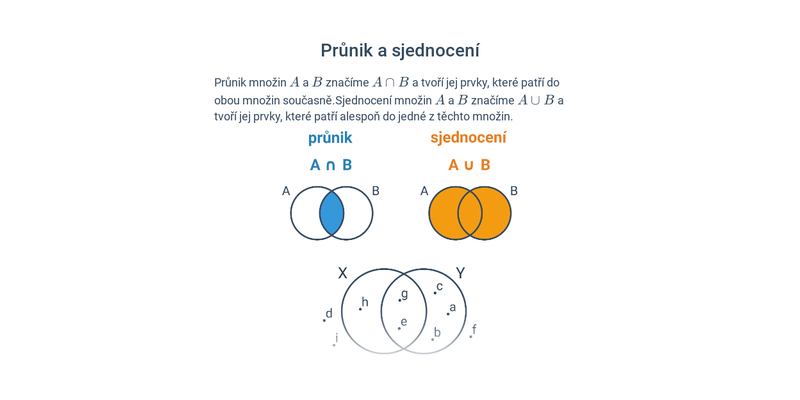
Průnik množin značíme takovýmto symbolem ∩ a můžeme jej chápat jako logickou spojku a zároveň. Protože průnik vybírá z množin ty prvky, které jsou v obou množinách zároveň. Také trochu připomíná logickou spojku a zároveň.

Co je to základní množina : Množina se dá chápat jako soubor prvků. Každá množina tedy obsahuje určitý počet prvků, který může být konečný nebo nekonečný. Též nemusí obsahovat prvek žádný, poté mluvíme o prázdné množině.

Množina je soubor objektů, chápaný jako celek. Objekty množiny se nazývají prvky množiny. Charakterizující vlastnost množiny je, že je jednoznačně určena svými prvky (ale nevšímá si jejich pořadí ani žádné další struktury). Množina, neobsahující žádné prvky se nazývá prázdná množina.

Množina, označení

Toto pravidlo mívá mnoho podob: výrok, matematickou formuli,výčet prvků apod. Definice: Množina se nazývá konečná, má-li konečně mnoho prvků. Každá množina, která není konečná, je nekonečná. Přitom konečná množina s nulovým počtem prvků se nazývá prázdná množina a označuje se ∅, {∅} nebo jen {}.

Jak se pozná doplněk

Jak poznat doplněk

Doplněk se váže na dva větné členy zároveň. Tím je unikátní. Jednou z vazeb je vždy vazba na přísudek. Druhá vazba je spojení buď s podmětem (Chlapec ležel nemocen), nebo s předmětem (Našli jsme ho promrzlého).Množina je soubor prvků. Množiny využíváme jako dílčí prvek v mnoha oblastech matematiky. Příklad z geometrie: kružnice je množina bodů, které mají stejnou vzdálenost od středu. Množiny mají i mnoho praktických využití.Následně 18. února 1861 hrabě Camilo Cavour vyhlásil zřízení Italského království, skládajícího se ze severní i jižní Itálie. Král Viktor Emanuel II. Piemontsko-sardinský ze Savojské dynastie byl prohlášen italským králem.

Tato operace se jmenuje sjednocení a značíme ji „\cup“. Definice je následující: Množina A\cup B obsahuje jen a pouze takové prvky, které patří alespoň do jedné z množin A a B. Sjednocením dvou množin tedy získáme množinu, která obsahuje všechny prvky z obou těchto množin.

Co to je Adult : adult {přídavné jméno}

dospělý {příd. jm. m.}

Jak zapsat prázdnou množinu : Prvky značíme malými písmeny. Prázdnou množinu značíme { } nebo Ř. Písmena N; Z; Q; R jsou používána pro označení číselných oborů: množina přirozených čísel N = { 1; 2; 3; 4; 5; 6;…}

Jak napsat prázdnou množinu

Prvky značíme malými písmeny. Prázdnou množinu značíme { } nebo Ř. Písmena N; Z; Q; R jsou používána pro označení číselných oborů: množina přirozených čísel N = { 1; 2; 3; 4; 5; 6;…}

Chceme-li zapsat, že nějaký prvek x patří do množiny M, využijeme značku \in a zapíšeme tento fakt jako x \in M. Pokud naopak nějaký prvek y do množiny M nenáleží, můžeme použít zápis „y \notin M“. Často se také používá grafické znázornění množin, které umožňuje objasnění některých vztahů a pojmů.Množiny vždy zapisujeme do složených závorek, prakticky vždy, když uvidíte složené závorky, jedná se o nějakou množinu. Množina může být pochopitelně prázdná, k tomu slouží buď zápis P={} nebo jednodušeji P = ∅ P=\varnothing P=∅.