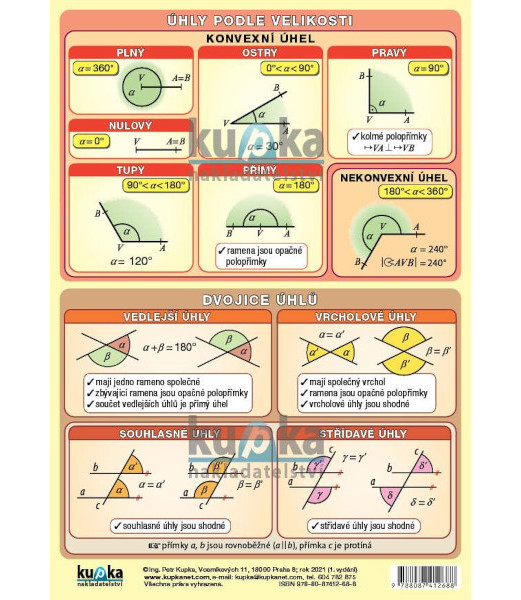
dvojice úhlů, jejichž ramena jsou opačné polopřímky
vedlejší úhly
dvojice úhlů, jejichž jedno rameno je společné a druhá ramena jsou opačné polopřímky
Konkávní úhel je úhel, který měří více než 180 ° nebo π radiánů, to znamená, že je větší než přímý úhel a menší než úplný úhel 360 °. Musíme si pamatovat, že úhel je ten oblouk, který je tvořen křížením dvou paprsků, linií nebo segmentů.Prázdnou množinu a jednobodové množiny považujeme také za konvexní. Symbolicky zapsáno: M je konvexní množina ⇔ (∀X, Y ∈ M)[XY ⊂ M ∨ M = ∅ ∨ M = {X}]. Množina bodů, která není konvexní se nazývá nekonvexní.
Jaké jsou druhy úhlu : Ukážeme si základní druhy úhlů a trochu podrobněji si vysvětlíme, jaké mají vlastnosti. Ostré úhly měří méně než 90 stupňů. Pravé úhly měří 90 stupňů. Tupé úhly měří více než 90 stupňů.
Jaký úhel má 180 stupňů
Jeden stupeň je 1/180 přímého úhlu, neboli přímý úhel má velikost 180°.
Proč má kruh 360 stupňů : Není však jasné, proč Babyloňané kruh rozdělili právě na 360 stupňů, tedy 6 × 60. Podle různých teorií byl důvod astronomický (číslo blízké počtu dní v roce), matematický (číslo umožňovalo dobrou práci se zlomky) nebo geometrický (rozdělení kruhu šestiúhelníkem).
Jako konvexní (latinsky convexus vypouklý, vypuklý) se označují (například v matematice nebo optice) takové formy (plochy, křivky), které jsou vyklenuté směrem ven. Formy, které jsou naopak vyklenuté směrem dovnitř (tj. vyduté), se označují jako konkávní. Jako konkávní (vydutý) se označují (například v matematice nebo optice) takové formy (plochy nebo křivky), které jsou vyduté směrem dovnitř. Formy, které jsou vyklenuté směrem ven (tj. vypuklé), se označují jako konvexní.
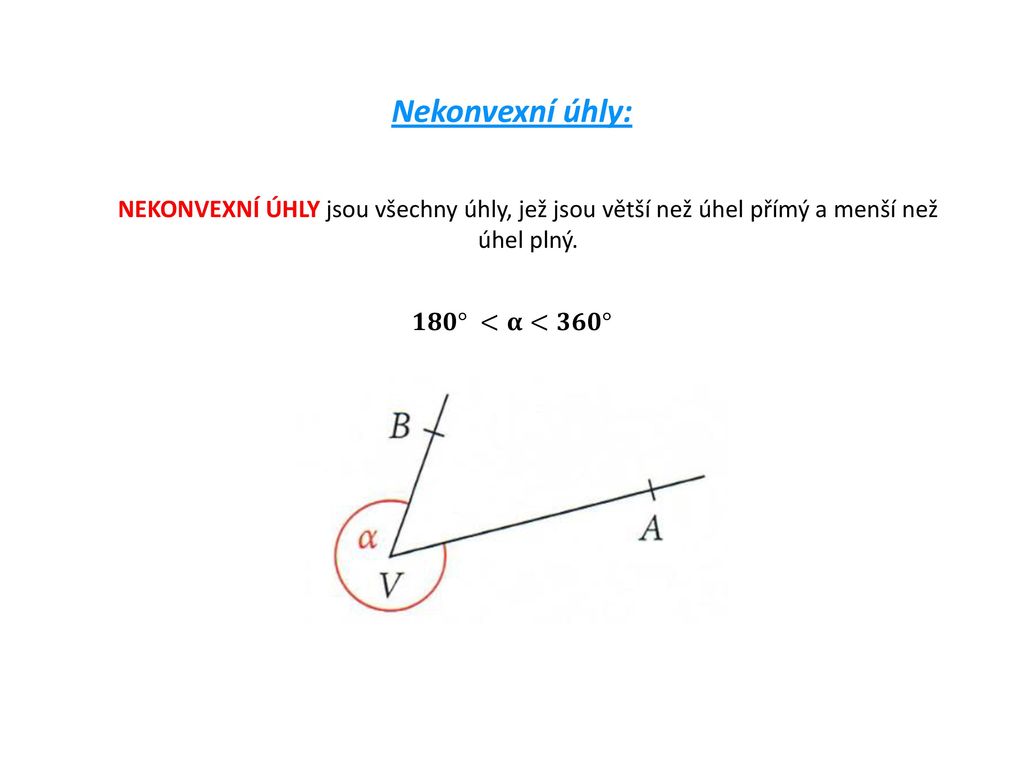
Co je to Nekonvexni úhel
Úhly, které nejsou konvexní, říkáme, že jsou nekonvexní. získáme výpočtem: β = 360°- a = 360° – 230° = 130°.Druhy úhlů
Nulový úhel (0°, 0 rad) je úhel, jehož ramena leží na sobě.
Ostrý úhel (< 90°, < /2 rad) je úhel menší než pravý úhel.
Pravý úhel (90°, /2) je polovina přímého úhlu.
Tupý úhel (> 90°, ale < 180°) je úhel větší než pravý úhel, ale menší než přímý úhel.
Přímý úhel (180°,
Plný úhel (360°, 2.
Pravý úhel je úhel, který tvoří polovinu přímého úhlu či čtvrtinu plného úhlu. Jeho numerická hodnota ve stupních je 90, v radiánech π/2, 100 v gradiánech. Název pravý úhel vznikl nepřesným překladem latinského termínu angulus rectus, kde ovšem slovo rectus bylo původně použito ve významu „vzpřímený“, nikoli „pravý“. Nejpopulárnější jednotka pro měření úhlu je stupeň. Máme 360 stupňů v plném kruhu, 90 stupňů je pravý úhel.
Proč je 360 stupňů : Není však jasné, proč Babyloňané kruh rozdělili právě na 360 stupňů, tedy 6 × 60. Podle různých teorií byl důvod astronomický (číslo blízké počtu dní v roce), matematický (číslo umožňovalo dobrou práci se zlomky) nebo geometrický (rozdělení kruhu šestiúhelníkem).
Kolik je 1 stupeň : Jeden stupeň má 60 minut a minuta se dále dělí na 60 vteřin, tedy stupeň má 3 600 vteřin: 1° = 60′ = 3600″ Úhlové stupně se používají mimo jiné ve sférických soustavách souřadnic, ke kterým patří zeměpisné souřadnice a různé systémy používané v astronomii.
Kolik je 1 Radián stupňů
1 radián je roven (180 děleno π) stupňů. Konvexita je veličina, která upřesňuje informaci, kterou poskytuje durace. Vztah mezi mírou výnosu do doby splatnosti a cenou oblikace není totiž lineární, ale konvexně zakřivený. Míru tohoto zakřivení udává právě konvexita.Funkce je konvexní na nějakém intervalu přesně tehdy, jestliže kdykoliv nakreslíme tečnu ke grafu v nějakém bodě tohoto intervalu, pak graf (přesněji jeho část odpovídající tomuto intervalu konvexity) leží na nebo nad touto tečnou.
Kdy je funkce konvexní : Konvexní a konkávní funkce. Konvexní funkce f je taková funkce, která má derivaci v bodě x0, body grafu funkce f "leží nad tečnou", f ´´(x0) > 0. Konkávní funkce f je taková funkce, která má derivaci v bodě x0, body grafu funkce f "leží pod tečnou", f ´´(x0) < 0.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Co je to Nekonvexni úhel? Weitere Antworten – Kolik má konvexní úhel stupňů
umime.to/F4K
Konkávní úhel je úhel, který měří více než 180 ° nebo π radiánů, to znamená, že je větší než přímý úhel a menší než úplný úhel 360 °. Musíme si pamatovat, že úhel je ten oblouk, který je tvořen křížením dvou paprsků, linií nebo segmentů.Prázdnou množinu a jednobodové množiny považujeme také za konvexní. Symbolicky zapsáno: M je konvexní množina ⇔ (∀X, Y ∈ M)[XY ⊂ M ∨ M = ∅ ∨ M = {X}]. Množina bodů, která není konvexní se nazývá nekonvexní.
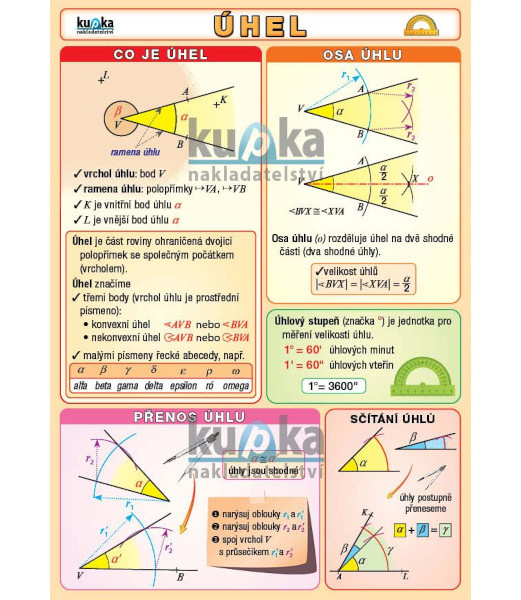
Jaké jsou druhy úhlu : Ukážeme si základní druhy úhlů a trochu podrobněji si vysvětlíme, jaké mají vlastnosti. Ostré úhly měří méně než 90 stupňů. Pravé úhly měří 90 stupňů. Tupé úhly měří více než 90 stupňů.
Jaký úhel má 180 stupňů
Jeden stupeň je 1/180 přímého úhlu, neboli přímý úhel má velikost 180°.
Proč má kruh 360 stupňů : Není však jasné, proč Babyloňané kruh rozdělili právě na 360 stupňů, tedy 6 × 60. Podle různých teorií byl důvod astronomický (číslo blízké počtu dní v roce), matematický (číslo umožňovalo dobrou práci se zlomky) nebo geometrický (rozdělení kruhu šestiúhelníkem).
Jako konvexní (latinsky convexus vypouklý, vypuklý) se označují (například v matematice nebo optice) takové formy (plochy, křivky), které jsou vyklenuté směrem ven. Formy, které jsou naopak vyklenuté směrem dovnitř (tj. vyduté), se označují jako konkávní.
Jako konkávní (vydutý) se označují (například v matematice nebo optice) takové formy (plochy nebo křivky), které jsou vyduté směrem dovnitř. Formy, které jsou vyklenuté směrem ven (tj. vypuklé), se označují jako konvexní.
Co je to Nekonvexni úhel
Úhly, které nejsou konvexní, říkáme, že jsou nekonvexní. získáme výpočtem: β = 360°- a = 360° – 230° = 130°.Druhy úhlů
Pravý úhel je úhel, který tvoří polovinu přímého úhlu či čtvrtinu plného úhlu. Jeho numerická hodnota ve stupních je 90, v radiánech π/2, 100 v gradiánech. Název pravý úhel vznikl nepřesným překladem latinského termínu angulus rectus, kde ovšem slovo rectus bylo původně použito ve významu „vzpřímený“, nikoli „pravý“.
Nejpopulárnější jednotka pro měření úhlu je stupeň. Máme 360 stupňů v plném kruhu, 90 stupňů je pravý úhel.
Proč je 360 stupňů : Není však jasné, proč Babyloňané kruh rozdělili právě na 360 stupňů, tedy 6 × 60. Podle různých teorií byl důvod astronomický (číslo blízké počtu dní v roce), matematický (číslo umožňovalo dobrou práci se zlomky) nebo geometrický (rozdělení kruhu šestiúhelníkem).
Kolik je 1 stupeň : Jeden stupeň má 60 minut a minuta se dále dělí na 60 vteřin, tedy stupeň má 3 600 vteřin: 1° = 60′ = 3600″ Úhlové stupně se používají mimo jiné ve sférických soustavách souřadnic, ke kterým patří zeměpisné souřadnice a různé systémy používané v astronomii.
Kolik je 1 Radián stupňů
1 radián je roven (180 děleno π) stupňů.
Konvexita je veličina, která upřesňuje informaci, kterou poskytuje durace. Vztah mezi mírou výnosu do doby splatnosti a cenou oblikace není totiž lineární, ale konvexně zakřivený. Míru tohoto zakřivení udává právě konvexita.Funkce je konvexní na nějakém intervalu přesně tehdy, jestliže kdykoliv nakreslíme tečnu ke grafu v nějakém bodě tohoto intervalu, pak graf (přesněji jeho část odpovídající tomuto intervalu konvexity) leží na nebo nad touto tečnou.
Kdy je funkce konvexní : Konvexní a konkávní funkce. Konvexní funkce f je taková funkce, která má derivaci v bodě x0, body grafu funkce f "leží nad tečnou", f ´´(x0) > 0. Konkávní funkce f je taková funkce, která má derivaci v bodě x0, body grafu funkce f "leží pod tečnou", f ´´(x0) < 0.