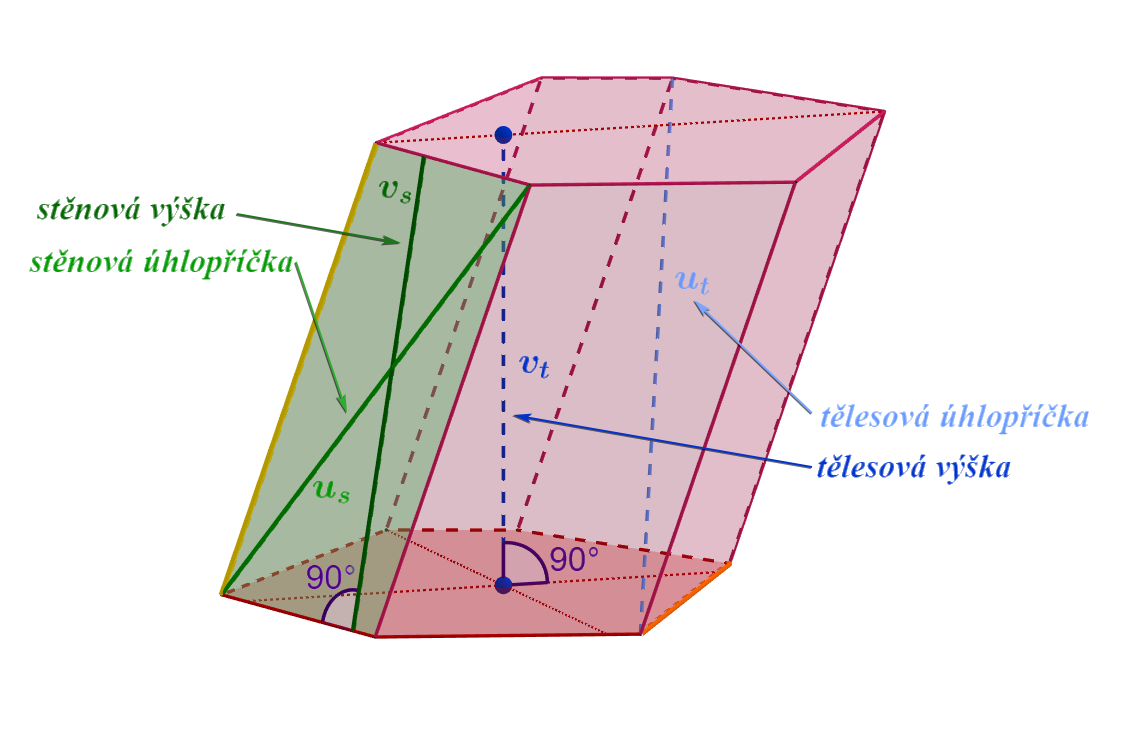
V tělesech se rozlišuje stěnová výška a tělesová výška. Stěnová výška je kolmice spuštěná z vrcholu na protější hrany; stěnová výška leží na stěně tělesa. Tělesová výška je kolmice spuštěná z vrcholu na protější stěnu.Tvar jehlanu mají egyptské pyramidy, stan, věže kostelů, hradů atd. = jehlan, jehož podstavou je čtverec a boční stěny jsou rovnoramenné trojúhelníky.Vzorec pro výpočet objemu jehlanu
Objem jehlanu se spočítá jako obsah podstavy [Sp] krát výška jehlanu [v] lomeno třemi. Přičemž obsah podstavy [Sp] vypočítáme vzorcem pro obsah čtverce, tedy a2.
Kolik má jehlan stěn : Vlastnosti: \bullet Jehlan má vždy tolik stěn, kolik má jeho podstava hran plus jedna, tzn. že čtyřboký jehlan má pět stěn (čtyři stěny tvoří plášť a jedna stěna podstavu), pětiboký šest, šestiboký sedm atd…
Co je výška v geometrii
Výška trojúhelníku je vzdálenost vrcholu trojúhelníku od protější strany. Je to úsečka, jejíž jeden krajní bod je vrchol a je kolmá na protější stranu k tomuto vrcholu. Každý trojúhelník má tři výšky. Přímky, na kterých leží výšky, se protínají v jednom společném bodě.
Jak se značí výšky : Výšky označujeme malým písmenem v s dolním indexem, kde vložíme označení, z kterého vrcholu výška vede. V případě výšky BPb tak mluvíme o výšce vb. Průsečík výšek je označen zeleným bodem V. V případě tupoúhlého trojúhelníku leží průsečík výšek mimo trojúhelník.
Jehlan je trojrozměrné těleso. Jeho základnu (nebo také podstavu) tvoří mnohoúhelník. Vrcholy základny jsou spojeny s jedním bodem mimo rovinu základny – tento bod se obvykle nazývá (hlavní) vrchol jehlanu. Kolmá vzdálenost vrcholu od roviny podstavy se nazývá výška jehlanu. Trojboký jehlan, což je jehlan s nejmenším počtem stěn čtyři, nazýváme čtyřstěn (obr. 4.4.1). Jsou-li jeho stěny tvořeny čtyřmi navzájem shodnými rovnostrannými trojúhelníky, jedná se o pravidelný čtyřstěn (pravidelný tetraedr, viz obr.
Jak se počítá kvádr
U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c).jehlan
obsah podstavy S p = 1 4 n a 2 cot
kružnice opsaná (poloměr) r o = a 2 ⋅ sin
kružnice vepsaná (poloměr) r v = a 2 ⋅ tan
umime.to/FV6
mnohostěn
počet stěn
počet hran
čtyřstěn
4
6
krychle
6
12
osmistěn
8
12
dvanáctistěn
12
30
Čtyřstěn (zvaný též trojboký jehlan, tetraedr) je nejjednodušší mnohostěn, typ trojrozměrného tělesa. Je vymezen nejmenším možným počtem bodů, který může trojrozměrné těleso definovat, tzn. čtyřmi různými body v prostoru. Obecný čtyřstěn je tvořen ze čtyř obecných trojúhelníků.
Co to je výška : Výška označuje obvykle vertikální vzdálenost dvou bodů, tj. nad určitou úrovní (vzhůru). Vzdálenost pod danou úrovní (dolů) bývá označována jako hloubka. Společně s délkou a šířkou slouží k určení rozměrů v trojrozměrném prostoru.
Co znamená výška trojúhelníku : Výška trojúhelníku je kolmá vzdálenost strany a protějšího (příslušného) vrcholu (úsečka spojující vrchol trojúhelníku s patou kolmice vedené tímto vrcholem k jeho protější straně).
Jak se dělají výšky
Výšky se rýsují celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice procházela právě bodem C. Výšku můžeme vést z každého vrcholu trojúhelníka. Všechny výšky se pak protínají v bodě, které se nazývá průsečík výšek. Čtyřstěn (zvaný též trojboký jehlan, tetraedr) je nejjednodušší mnohostěn, typ trojrozměrného tělesa. Je vymezen nejmenším možným počtem bodů, který může trojrozměrné těleso definovat, tzn. čtyřmi různými body v prostoru.Stěny pravidelného čtyřstěnu jsou tvořeny čtyřmi shodnými rovnostrannými trojúhelníky. Toto těleso má čtyři vrcholy a šest hran, viz obr.
Kolik má trojboký hranol stěn : Trojboký hranol je těleso ohraničené dvěma shodnými trojúhelníky – horní a dolní podstava hranolu – a třemi bočními stěnami, které jsou buď obdélníky, nebo čtverce. Tyto tři stěny tvoří plášť hranolu. Těleso má šest podstavných hran (to jsou strany podstav) a tři boční hrany.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Co je stěnová výška? Weitere Antworten – Co je to Tělesová výška
V tělesech se rozlišuje stěnová výška a tělesová výška. Stěnová výška je kolmice spuštěná z vrcholu na protější hrany; stěnová výška leží na stěně tělesa. Tělesová výška je kolmice spuštěná z vrcholu na protější stěnu.Tvar jehlanu mají egyptské pyramidy, stan, věže kostelů, hradů atd. = jehlan, jehož podstavou je čtverec a boční stěny jsou rovnoramenné trojúhelníky.Vzorec pro výpočet objemu jehlanu
Objem jehlanu se spočítá jako obsah podstavy [Sp] krát výška jehlanu [v] lomeno třemi. Přičemž obsah podstavy [Sp] vypočítáme vzorcem pro obsah čtverce, tedy a2.
Kolik má jehlan stěn : Vlastnosti: \bullet Jehlan má vždy tolik stěn, kolik má jeho podstava hran plus jedna, tzn. že čtyřboký jehlan má pět stěn (čtyři stěny tvoří plášť a jedna stěna podstavu), pětiboký šest, šestiboký sedm atd…
Co je výška v geometrii
Výška trojúhelníku je vzdálenost vrcholu trojúhelníku od protější strany. Je to úsečka, jejíž jeden krajní bod je vrchol a je kolmá na protější stranu k tomuto vrcholu. Každý trojúhelník má tři výšky. Přímky, na kterých leží výšky, se protínají v jednom společném bodě.
Jak se značí výšky : Výšky označujeme malým písmenem v s dolním indexem, kde vložíme označení, z kterého vrcholu výška vede. V případě výšky BPb tak mluvíme o výšce vb. Průsečík výšek je označen zeleným bodem V. V případě tupoúhlého trojúhelníku leží průsečík výšek mimo trojúhelník.
Jehlan je trojrozměrné těleso. Jeho základnu (nebo také podstavu) tvoří mnohoúhelník. Vrcholy základny jsou spojeny s jedním bodem mimo rovinu základny – tento bod se obvykle nazývá (hlavní) vrchol jehlanu. Kolmá vzdálenost vrcholu od roviny podstavy se nazývá výška jehlanu.
Trojboký jehlan, což je jehlan s nejmenším počtem stěn čtyři, nazýváme čtyřstěn (obr. 4.4.1). Jsou-li jeho stěny tvořeny čtyřmi navzájem shodnými rovnostrannými trojúhelníky, jedná se o pravidelný čtyřstěn (pravidelný tetraedr, viz obr.
Jak se počítá kvádr
U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c).jehlan
umime.to/FV6
Čtyřstěn (zvaný též trojboký jehlan, tetraedr) je nejjednodušší mnohostěn, typ trojrozměrného tělesa. Je vymezen nejmenším možným počtem bodů, který může trojrozměrné těleso definovat, tzn. čtyřmi různými body v prostoru. Obecný čtyřstěn je tvořen ze čtyř obecných trojúhelníků.
Co to je výška : Výška označuje obvykle vertikální vzdálenost dvou bodů, tj. nad určitou úrovní (vzhůru). Vzdálenost pod danou úrovní (dolů) bývá označována jako hloubka. Společně s délkou a šířkou slouží k určení rozměrů v trojrozměrném prostoru.
Co znamená výška trojúhelníku : Výška trojúhelníku je kolmá vzdálenost strany a protějšího (příslušného) vrcholu (úsečka spojující vrchol trojúhelníku s patou kolmice vedené tímto vrcholem k jeho protější straně).
Jak se dělají výšky
Výšky se rýsují celkem snadno, vezmete si pravítko a vedete kolmici ze strany c tak, aby tato kolmice procházela právě bodem C. Výšku můžeme vést z každého vrcholu trojúhelníka. Všechny výšky se pak protínají v bodě, které se nazývá průsečík výšek.
Čtyřstěn (zvaný též trojboký jehlan, tetraedr) je nejjednodušší mnohostěn, typ trojrozměrného tělesa. Je vymezen nejmenším možným počtem bodů, který může trojrozměrné těleso definovat, tzn. čtyřmi různými body v prostoru.Stěny pravidelného čtyřstěnu jsou tvořeny čtyřmi shodnými rovnostrannými trojúhelníky. Toto těleso má čtyři vrcholy a šest hran, viz obr.
Kolik má trojboký hranol stěn : Trojboký hranol je těleso ohraničené dvěma shodnými trojúhelníky – horní a dolní podstava hranolu – a třemi bočními stěnami, které jsou buď obdélníky, nebo čtverce. Tyto tři stěny tvoří plášť hranolu. Těleso má šest podstavných hran (to jsou strany podstav) a tři boční hrany.