Normální rozdělení neboli Gaussovo rozdělení (podle Carla Friedricha Gausse) je jedno z nejdůležitějších rozdělení pravděpodobnosti spojité náhodné veličiny. (Slovo „normální“ zde není použito v nejběžnějším smyslu „obyčejné, běžné“, ale znamená „řídící se zákonem, předpisem nebo modelem“.)Hustota pravděpodobnosti (hustota rozdělení pravděpodobnosti, anglicky Probability Density Function, PDF) v teorii pravděpodobnosti je funkce, jejíž integrací na kterémkoli vzorku (podmnožině prostoru elementárních jevů) vyjde relativní pravděpodobnost, že hodnota náhodné proměnné by se rovnala tomuto vzorku.V posloupnosti n vzájemně nezávislých pokusů pozorujeme počet nastoupení sledovaného jevu, který v každém pokusu nastává s pravděpodobností p.
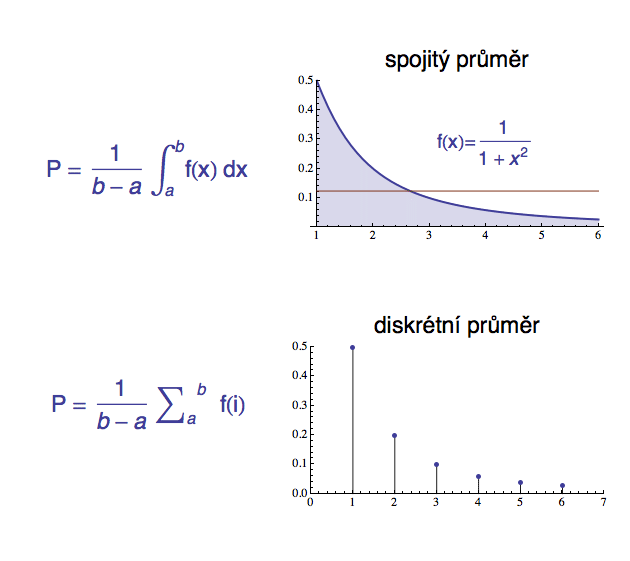
Jak urcit distribucni funkcí : Distribuční funkce F(xi) je tedy vždy přiřazena ke konkrétní hodnotě náhodné veličiny xi. Chování diskrétní náhodné veličiny lze popsat pravděpodobnostní funkcí p(x)= P(X = x). Známe-li pravděpodobnostní funkci, umíme dopočítat distribuční funkci, a naopak.
Jak zjistit normální rozdělení
Normální rozdělení plně charakterizují dvě konstanty: střední hodnota μ a rozptyl σ2. Pokud chceme napsat, že náhodná veličina X (tedy např. výsledek pokusu) má náhodné rozdělení se střední hodnotou μ a rozptylem σ2, obvykle použijeme označení: X ∼ N ( μ , σ 2 ) {\displaystyle X\ \sim \ N(\mu ,\sigma ^{2})}
Co je diskrétní veličina : Diskrétní (nespojitá) náhodná veličina – taková, která může nabývat pouze jednotlivých hodnot (celých čísel) z konečného nebo nekonečného intervalu, tzn. může se měnit jen po skocích.
objem V. Pro výpočet platí vztah: hustota = hmotnost tělesa vydělíme objemem tělesa ρ = m/V. hustota ρ je v kilogramech na metr krychlový (kg/m3). Pokud je hmotnost m v gramech (g) a objem V v centimetrech krychlových (cm3), potom hustota je v gramech na centimetr krychlový (g/cm3). Náhodná veličina X má binomické rozdělení Bi(n, p) právě tehdy, když je pravděpodobnostní funkce určena vztahem: , kde x = 0, 1, …, n; n je počet pokusů a p je pravděpodobnost úspěšnosti v každém pokusu.
Jak poznat poissonovo rozdělení
U Poissonova rozdělení je typické, že se podle něj řídí četnosti událostí, které ale jsou poměrně vzácné − mají tedy velmi malou pravděpodobnost výskytu (například se může jednat o počet krvácivých událostí u sledovaných osob za 100 osobo-roků aj.).Pro ověření normality jednorozměrných dat je možné použít grafické metody i statistické testy. Z grafických metod se používá vykreslení histogramu či Q-Q diagramu a ke statistickému testování můžeme zvolit Shapirův-Wilkův test či Kolmogorovův-Smirnovovův test .Náhodná veličina představuje číselné vyjádření výsledku náhodného pokusu, matematicky řečeno je to funkce, která každému elementárnímu jevu ωi z Ω přiřadí hodnotu X(ωi) z množiny možných hodnot (ta je podmnožinou množiny reálných čísel, R). Pro výpočet platí vztah: hustota = hmotnost tělesa vydělíme objemem tělesa ρ = m/V. Pokud je hmotnost m v kilogramech (kg) a objem V v metrech krychlových (m3), potom hustota ρ je v kilogramech na metr krychlový (kg/m3).
Co to je hustota : Hustota jako fyzikální veličina má značku ρ (řecké písmeno ró) a její zálkadní jednotkou je kg/m3. Další jednotkou je například g/cm3. Hustota nám tedy říká, kolik kg by daná látka vážila, pokud bychom jí měli 1 m3 (tj. krychli o straně 1 metr).
Kdy použít poissonovo rozdělení : Velký význam má Poissonovo rozdělení v teorii hromadné obsluhy, kde popisuje takové náhodné jevy, jako jsou příchody zákazníků. Počet pulsů registrovaných GM-trubicí za zvolený časový interval. Počet aut, která projedou určitým místem za daný čas. Počet branek za fotbalový zápas.
Jak zjistit normální rozdělení dat
Jednoduchý způsob, jak alespoň přibližně odhadnout, zda data mají normální rozdělení, je sestrojení histogramu. O něco přesnější je použití Q-Q grafu (kvantil-kvantil) nebo P-P grafu (pravděpodobnost-pravděpodobnost). Rozptyl σ2 je průměrem druhých mocnin odchylek jednotlivých hodnot od aritmetického průměru z hodnot statistického souboru. prostý aritmetický průměr. Rozptyl je ukazatelem variability (měnlivosti).minimálka) s tím, že 1 m3 = 1000 kg. Zároveň pokud je váha v tunách vetší než objem v kubických metrech účtuje se 1 tuna jako 1 kubický metr (např.
Jak se převádí g cm3 na kg m3 : Gram na centimetr krychlový je jednotkou hustoty a dílčí jednotkou kilogramu na metr krychlový. Jeden gram na centimetr krychlový odpovídá 1 000 kilogramům na metr krychlový a vyjadřuje hmotnost tělesa vztaženou k jeho objemu.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Co je diskrétní hodnota? Weitere Antworten – Co je to normální rozdělení
Normální rozdělení neboli Gaussovo rozdělení (podle Carla Friedricha Gausse) je jedno z nejdůležitějších rozdělení pravděpodobnosti spojité náhodné veličiny. (Slovo „normální“ zde není použito v nejběžnějším smyslu „obyčejné, běžné“, ale znamená „řídící se zákonem, předpisem nebo modelem“.)Hustota pravděpodobnosti (hustota rozdělení pravděpodobnosti, anglicky Probability Density Function, PDF) v teorii pravděpodobnosti je funkce, jejíž integrací na kterémkoli vzorku (podmnožině prostoru elementárních jevů) vyjde relativní pravděpodobnost, že hodnota náhodné proměnné by se rovnala tomuto vzorku.V posloupnosti n vzájemně nezávislých pokusů pozorujeme počet nastoupení sledovaného jevu, který v každém pokusu nastává s pravděpodobností p.
Jak urcit distribucni funkcí : Distribuční funkce F(xi) je tedy vždy přiřazena ke konkrétní hodnotě náhodné veličiny xi. Chování diskrétní náhodné veličiny lze popsat pravděpodobnostní funkcí p(x)= P(X = x). Známe-li pravděpodobnostní funkci, umíme dopočítat distribuční funkci, a naopak.
Jak zjistit normální rozdělení
Normální rozdělení plně charakterizují dvě konstanty: střední hodnota μ a rozptyl σ2. Pokud chceme napsat, že náhodná veličina X (tedy např. výsledek pokusu) má náhodné rozdělení se střední hodnotou μ a rozptylem σ2, obvykle použijeme označení: X ∼ N ( μ , σ 2 ) {\displaystyle X\ \sim \ N(\mu ,\sigma ^{2})}
Co je diskrétní veličina : Diskrétní (nespojitá) náhodná veličina – taková, která může nabývat pouze jednotlivých hodnot (celých čísel) z konečného nebo nekonečného intervalu, tzn. může se měnit jen po skocích.
objem V. Pro výpočet platí vztah: hustota = hmotnost tělesa vydělíme objemem tělesa ρ = m/V. hustota ρ je v kilogramech na metr krychlový (kg/m3). Pokud je hmotnost m v gramech (g) a objem V v centimetrech krychlových (cm3), potom hustota je v gramech na centimetr krychlový (g/cm3).
Náhodná veličina X má binomické rozdělení Bi(n, p) právě tehdy, když je pravděpodobnostní funkce určena vztahem: , kde x = 0, 1, …, n; n je počet pokusů a p je pravděpodobnost úspěšnosti v každém pokusu.
Jak poznat poissonovo rozdělení
U Poissonova rozdělení je typické, že se podle něj řídí četnosti událostí, které ale jsou poměrně vzácné − mají tedy velmi malou pravděpodobnost výskytu (například se může jednat o počet krvácivých událostí u sledovaných osob za 100 osobo-roků aj.).Pro ověření normality jednorozměrných dat je možné použít grafické metody i statistické testy. Z grafických metod se používá vykreslení histogramu či Q-Q diagramu a ke statistickému testování můžeme zvolit Shapirův-Wilkův test či Kolmogorovův-Smirnovovův test .Náhodná veličina představuje číselné vyjádření výsledku náhodného pokusu, matematicky řečeno je to funkce, která každému elementárnímu jevu ωi z Ω přiřadí hodnotu X(ωi) z množiny možných hodnot (ta je podmnožinou množiny reálných čísel, R).
Pro výpočet platí vztah: hustota = hmotnost tělesa vydělíme objemem tělesa ρ = m/V. Pokud je hmotnost m v kilogramech (kg) a objem V v metrech krychlových (m3), potom hustota ρ je v kilogramech na metr krychlový (kg/m3).
Co to je hustota : Hustota jako fyzikální veličina má značku ρ (řecké písmeno ró) a její zálkadní jednotkou je kg/m3. Další jednotkou je například g/cm3. Hustota nám tedy říká, kolik kg by daná látka vážila, pokud bychom jí měli 1 m3 (tj. krychli o straně 1 metr).
Kdy použít poissonovo rozdělení : Velký význam má Poissonovo rozdělení v teorii hromadné obsluhy, kde popisuje takové náhodné jevy, jako jsou příchody zákazníků. Počet pulsů registrovaných GM-trubicí za zvolený časový interval. Počet aut, která projedou určitým místem za daný čas. Počet branek za fotbalový zápas.
Jak zjistit normální rozdělení dat
Jednoduchý způsob, jak alespoň přibližně odhadnout, zda data mají normální rozdělení, je sestrojení histogramu. O něco přesnější je použití Q-Q grafu (kvantil-kvantil) nebo P-P grafu (pravděpodobnost-pravděpodobnost).
Rozptyl σ2 je průměrem druhých mocnin odchylek jednotlivých hodnot od aritmetického průměru z hodnot statistického souboru. prostý aritmetický průměr. Rozptyl je ukazatelem variability (měnlivosti).minimálka) s tím, že 1 m3 = 1000 kg. Zároveň pokud je váha v tunách vetší než objem v kubických metrech účtuje se 1 tuna jako 1 kubický metr (např.
Jak se převádí g cm3 na kg m3 : Gram na centimetr krychlový je jednotkou hustoty a dílčí jednotkou kilogramu na metr krychlový. Jeden gram na centimetr krychlový odpovídá 1 000 kilogramům na metr krychlový a vyjadřuje hmotnost tělesa vztaženou k jeho objemu.