Zero vector symbol is given by →0=(0,0,0) 0 → = ( 0 , 0 , 0 ) in three dimensional space and in a two-dimensional space, it written as →0=(0,0) 0 → = ( 0 , 0 ) . The components of a null vector are all equal to 0 as it has zero length and it does not point in any direction.Every vector space contains a zero vector. True. The existence of 0 is a requirement in the definition.Proof (a) Suppose that 0 and 0 are both zero vectors in V . Then x + 0 = x and x + 0 = x, for all x ∈ V . Therefore, 0 = 0 + 0, as 0 is a zero vector, = 0 + 0 , by commutativity, = 0, as 0 is a zero vector. Hence, 0 = 0 , showing that the zero vector is unique.
Is 0 vector unique : The two zero vectors are equal, which is a contraction to our assumption. Hence, the zero vector is unique. Therefore the given statement is true. Note: In vector space zero vector is always defined with respect to addition not with respect to multiplication.
Is 0 always in a vector space
There is only one zero-vector in a vector space. This does not need to be an axiom because it can be proven from the current 10 axioms as is done in the following theorem: c Matthew Bernstein 2017 1 Page 2 Theorem 1 Given vector space (V,F ), the zero vector is unique. Since a 0 , we reach a contradiction.
Can the zero vector be a vector space : The simplest example of a vector space is the trivial one: {0}, which contains only the zero vector (see the third axiom in the Vector space article). Both vector addition and scalar multiplication are trivial.
zeroes just like infinity, probable do not exist in the "real" world. There is not a single observed entity that has a no properties, by the very definition, if it did, it would be unobservable. The closest things to "zero" as we get is empty space, but quantum indeterminacy prohibits completely zero energy in space. Yes, when the 2 vectors are same in magnitude but opposite in direction. Then the resultant will be a null vector with zero magnitude. Q.
How do you prove zero vector exists
Proof (a) Suppose that 0 and 0 are both zero vectors in V . Then x + 0 = x and x + 0 = x, for all x ∈ V . Therefore, 0 = 0 + 0, as 0 is a zero vector, = 0 + 0 , by commutativity, = 0, as 0 is a zero vector. Hence, 0 = 0 , showing that the zero vector is unique.Zero vector has zero length so all its components are zero and it does not point in any direction. Let us understand this using a real-life example: Let us suppose two people are pulling a table towards themselves using the same amount of force. The force applied in this sense is equal but in the opposite direction.A zero vector or null vector is a vector in space with magnitude 0 and direction unknown. To write the zero vector sign in two dimensions, use the following formulas: A null vector has zero length and no direction. Hence its components are all 0. Zero is an intriguing number both mathematically and philosophically. Mathematically, a concept of zero plays an important role in our theories of natural, integer, and real numbers.
Why is 0 0 impossible : One can argue that 0/0 is 0, because 0 divided by anything is 0. Another one can argue that 0/0 is 1, because anything divided by itself is 1. And that's exactly the problem! Whatever we say 0/0 equals to, we contradict one crucial property of numbers or another.
Can a non zero vector have a zero : No, a vector cannot have zero magnitude if one of its components is not zero.
Why is zero vector not unique
The two zero vectors are equal, which is a contraction to our assumption. Hence, the zero vector is unique. Therefore the given statement is true. Note: In vector space zero vector is always defined with respect to addition not with respect to multiplication. Zero vector can be defined as a vector having zero magnitude and an arbitrary direction is called zero or null vector.Last Updated on May 2, 2023. A vector is stated to be a zero vector when the magnitude of the given vector is zero. This implies that the starting point of the vector matches the final point.
Is 0 0 meaningless : With reference to the example given above, if we consider 0 by 0 to X, i.e., 0/0=X, it can also be rewritten as 0*X=0, and the problem is that every number works. X could be anything, so this equation is not useful at all. Hence, If we divide by zero, it is considered as "Undefined."
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Can you have a zero vector? Weitere Antworten – How to find zero vector
Zero vector symbol is given by →0=(0,0,0) 0 → = ( 0 , 0 , 0 ) in three dimensional space and in a two-dimensional space, it written as →0=(0,0) 0 → = ( 0 , 0 ) . The components of a null vector are all equal to 0 as it has zero length and it does not point in any direction.Every vector space contains a zero vector. True. The existence of 0 is a requirement in the definition.Proof (a) Suppose that 0 and 0 are both zero vectors in V . Then x + 0 = x and x + 0 = x, for all x ∈ V . Therefore, 0 = 0 + 0, as 0 is a zero vector, = 0 + 0 , by commutativity, = 0, as 0 is a zero vector. Hence, 0 = 0 , showing that the zero vector is unique.
Is 0 vector unique : The two zero vectors are equal, which is a contraction to our assumption. Hence, the zero vector is unique. Therefore the given statement is true. Note: In vector space zero vector is always defined with respect to addition not with respect to multiplication.
Is 0 always in a vector space
There is only one zero-vector in a vector space. This does not need to be an axiom because it can be proven from the current 10 axioms as is done in the following theorem: c Matthew Bernstein 2017 1 Page 2 Theorem 1 Given vector space (V,F ), the zero vector is unique. Since a 0 , we reach a contradiction.
Can the zero vector be a vector space : The simplest example of a vector space is the trivial one: {0}, which contains only the zero vector (see the third axiom in the Vector space article). Both vector addition and scalar multiplication are trivial.
zeroes just like infinity, probable do not exist in the "real" world. There is not a single observed entity that has a no properties, by the very definition, if it did, it would be unobservable. The closest things to "zero" as we get is empty space, but quantum indeterminacy prohibits completely zero energy in space.
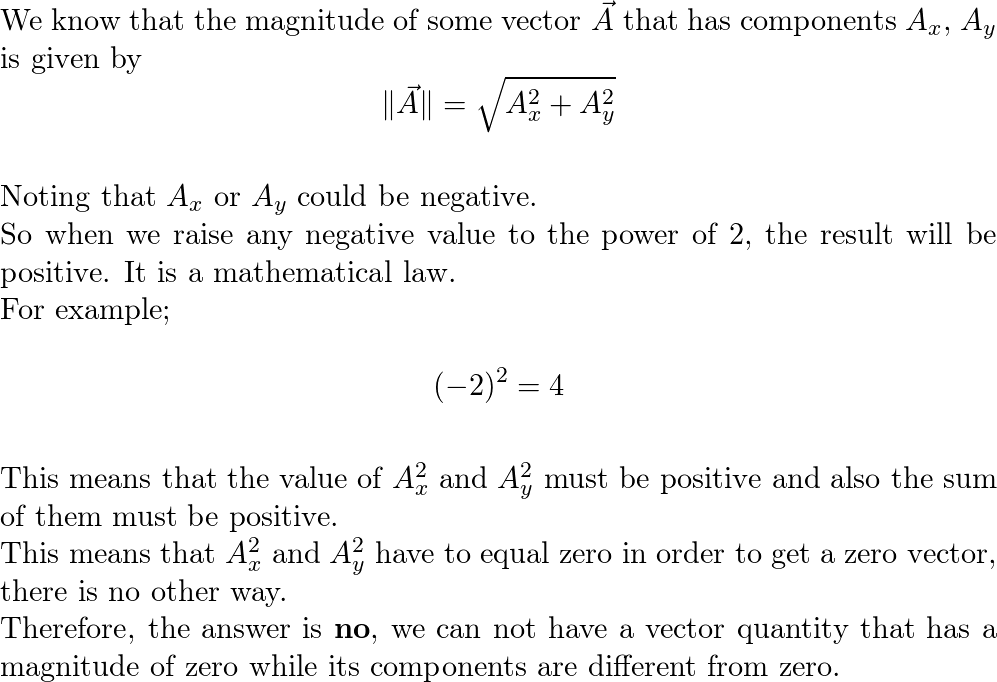
Yes, when the 2 vectors are same in magnitude but opposite in direction. Then the resultant will be a null vector with zero magnitude. Q.
How do you prove zero vector exists
Proof (a) Suppose that 0 and 0 are both zero vectors in V . Then x + 0 = x and x + 0 = x, for all x ∈ V . Therefore, 0 = 0 + 0, as 0 is a zero vector, = 0 + 0 , by commutativity, = 0, as 0 is a zero vector. Hence, 0 = 0 , showing that the zero vector is unique.Zero vector has zero length so all its components are zero and it does not point in any direction. Let us understand this using a real-life example: Let us suppose two people are pulling a table towards themselves using the same amount of force. The force applied in this sense is equal but in the opposite direction.A zero vector or null vector is a vector in space with magnitude 0 and direction unknown. To write the zero vector sign in two dimensions, use the following formulas: A null vector has zero length and no direction. Hence its components are all 0.
Zero is an intriguing number both mathematically and philosophically. Mathematically, a concept of zero plays an important role in our theories of natural, integer, and real numbers.
Why is 0 0 impossible : One can argue that 0/0 is 0, because 0 divided by anything is 0. Another one can argue that 0/0 is 1, because anything divided by itself is 1. And that's exactly the problem! Whatever we say 0/0 equals to, we contradict one crucial property of numbers or another.
Can a non zero vector have a zero : No, a vector cannot have zero magnitude if one of its components is not zero.
Why is zero vector not unique
The two zero vectors are equal, which is a contraction to our assumption. Hence, the zero vector is unique. Therefore the given statement is true. Note: In vector space zero vector is always defined with respect to addition not with respect to multiplication.
Zero vector can be defined as a vector having zero magnitude and an arbitrary direction is called zero or null vector.Last Updated on May 2, 2023. A vector is stated to be a zero vector when the magnitude of the given vector is zero. This implies that the starting point of the vector matches the final point.
Is 0 0 meaningless : With reference to the example given above, if we consider 0 by 0 to X, i.e., 0/0=X, it can also be rewritten as 0*X=0, and the problem is that every number works. X could be anything, so this equation is not useful at all. Hence, If we divide by zero, it is considered as "Undefined."