While this generates a single number, you can think of a single number as a 1 x 1 matrix, which, if non-zero, has rank 1.Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix: Swap the positions of two of the rows. Multiply one of the rows by a nonzero scalar.Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product.
Why is matrix rank 1 : The column space of A is R1. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1. 1 4 5 A = 2 8 10 2 Page 3 has rank 1 because each of its columns is a multiple of the first column.
What are the rules of Gaussian elimination
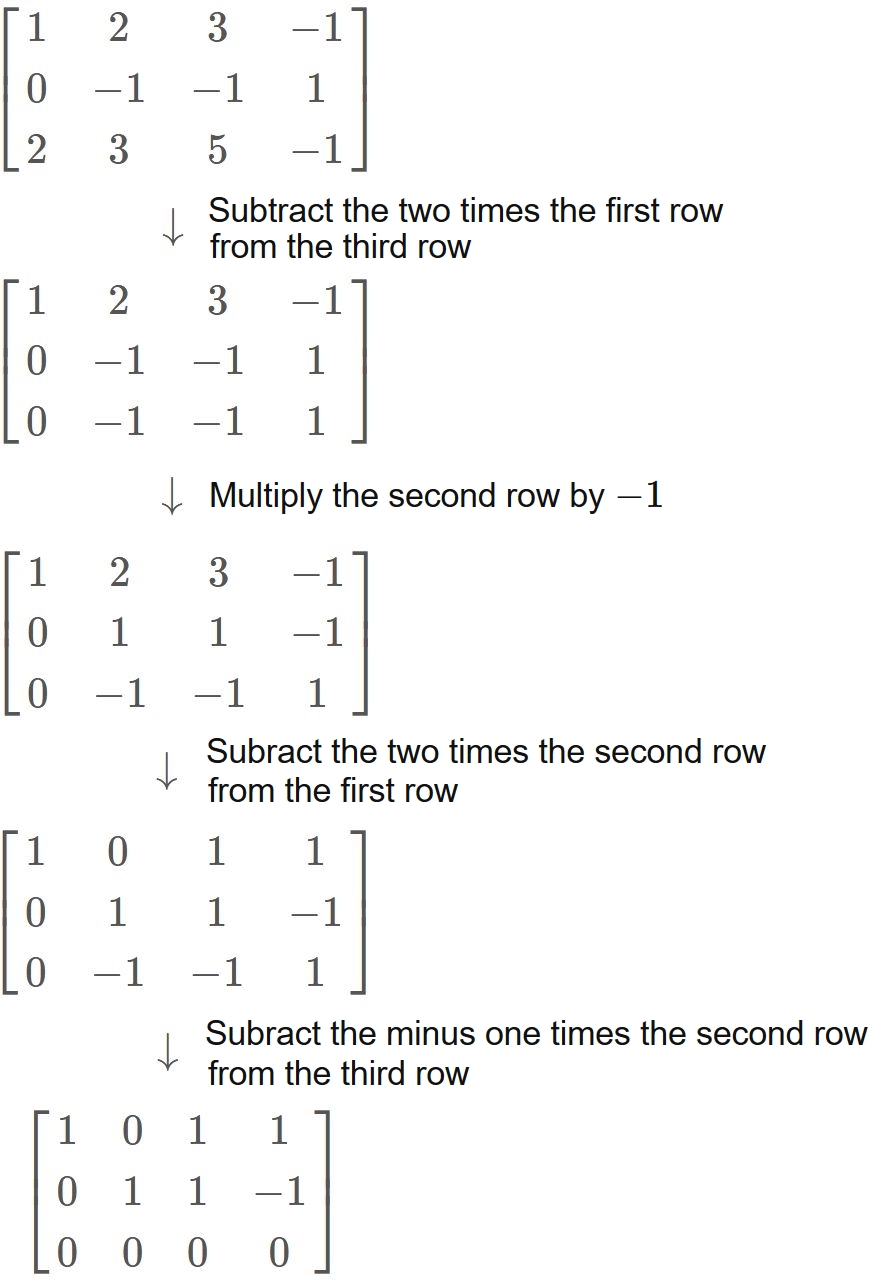
You can perform three operations on matrices in order to eliminate variables in a system of linear equations:
You can multiply any row by a constant (other than zero). multiplies row three by –2 to give you a new row three.
You can switch any two rows. swaps rows one and two.
You can add two rows together.
Does Gaussian elimination always work : Yes, Gaussian elimination always works for solving systems of linear equations, given that the system has a unique solution. However, if the system has no solution or an infinite number of solutions, Gaussian elimination will not provide a unique solution.
Since a zero determinant of any n x n matrix implies that the rank must be less than n, the rank for a 2×2 matrix must be 0 (null matrix) or 1. As a standard exercise in linear algebra, we can show that any rank-1 matrix may be written as the outer product of two vectors, a well-documented result in textbooks.
Here is an intuitive explanation: UVT will have a dimension of m x n. All the rows will be a linear combination(or multiples) of V i.e. Row Rank of the matrix is 1. All columns will be a linear combination (or multiples) of U i.e. Column Rank of the matrix is 1.
What is the rank of a matrix
The rank of the matrix refers to the number of linearly independent rows or columns in the matrix. ρ(A) is used to denote the rank of matrix A. A matrix is said to be of rank zero when all of its elements become zero. The rank of the matrix is the dimension of the vector space obtained by its columns.Yes, Gaussian elimination always works for solving systems of linear equations, given that the system has a unique solution. However, if the system has no solution or an infinite number of solutions, Gaussian elimination will not provide a unique solution.Gaussian elimination, as described above, fails if any of the pivots is zero, it is worse yet if any pivot becomes close to zero. In this case, the method can be carried to completion, but the obtained results may be totally wrong. A = ( 0.0001 1 1 1 ) , using three decimal digit floating point arithmetic.
Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
What is the rank of a 3×3 matrix : 3
For example, if we consider the identity matrix of order 3 × 3, all its rows (or columns) are linearly independent and hence its rank is 3.
Can a matrix have a rank of 1 : Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
What happens when the rank of a matrix is 1
Matrix A has only one linearly independent row, so its rank is 1. Hence, matrix A is not full rank.
The zero matrix is the only matrix whose rank is 0.Sure, you can have a matrix of rank 4, or 5 or 6 or any higher integer. It's just you need longer vectors, spaces of higher dimension than 3 (indeed the Cliff's notes explicitly state 3-vectors).
Can a 3×3 matrix have rank 0 : Recall that the rank of a matrix 𝐴 is equal to the number of rows/columns of the largest square submatrix of 𝐴 that has a nonzero determinant. Since this is a 3 × 3 matrix, its rank must be between 0 and 3. Also, since it is not the zero matrix, its rank cannot be 0.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Can the rank of a 3×3 matrix be 1? Weitere Antworten – What is the rank of a 1×1 matrix
While this generates a single number, you can think of a single number as a 1 x 1 matrix, which, if non-zero, has rank 1.Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix: Swap the positions of two of the rows. Multiply one of the rows by a nonzero scalar.Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads. We can express any rank-one matrix as an outer product.
Why is matrix rank 1 : The column space of A is R1. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1. 1 4 5 A = 2 8 10 2 Page 3 has rank 1 because each of its columns is a multiple of the first column.
What are the rules of Gaussian elimination
You can perform three operations on matrices in order to eliminate variables in a system of linear equations:
Does Gaussian elimination always work : Yes, Gaussian elimination always works for solving systems of linear equations, given that the system has a unique solution. However, if the system has no solution or an infinite number of solutions, Gaussian elimination will not provide a unique solution.
Since a zero determinant of any n x n matrix implies that the rank must be less than n, the rank for a 2×2 matrix must be 0 (null matrix) or 1. As a standard exercise in linear algebra, we can show that any rank-1 matrix may be written as the outer product of two vectors, a well-documented result in textbooks.
Here is an intuitive explanation: UVT will have a dimension of m x n. All the rows will be a linear combination(or multiples) of V i.e. Row Rank of the matrix is 1. All columns will be a linear combination (or multiples) of U i.e. Column Rank of the matrix is 1.
What is the rank of a matrix
The rank of the matrix refers to the number of linearly independent rows or columns in the matrix. ρ(A) is used to denote the rank of matrix A. A matrix is said to be of rank zero when all of its elements become zero. The rank of the matrix is the dimension of the vector space obtained by its columns.Yes, Gaussian elimination always works for solving systems of linear equations, given that the system has a unique solution. However, if the system has no solution or an infinite number of solutions, Gaussian elimination will not provide a unique solution.Gaussian elimination, as described above, fails if any of the pivots is zero, it is worse yet if any pivot becomes close to zero. In this case, the method can be carried to completion, but the obtained results may be totally wrong. A = ( 0.0001 1 1 1 ) , using three decimal digit floating point arithmetic.
Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
What is the rank of a 3×3 matrix : 3
For example, if we consider the identity matrix of order 3 × 3, all its rows (or columns) are linearly independent and hence its rank is 3.
Can a matrix have a rank of 1 : Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
What happens when the rank of a matrix is 1
Matrix A has only one linearly independent row, so its rank is 1. Hence, matrix A is not full rank.
The zero matrix is the only matrix whose rank is 0.Sure, you can have a matrix of rank 4, or 5 or 6 or any higher integer. It's just you need longer vectors, spaces of higher dimension than 3 (indeed the Cliff's notes explicitly state 3-vectors).
Can a 3×3 matrix have rank 0 : Recall that the rank of a matrix 𝐴 is equal to the number of rows/columns of the largest square submatrix of 𝐴 that has a nonzero determinant. Since this is a 3 × 3 matrix, its rank must be between 0 and 3. Also, since it is not the zero matrix, its rank cannot be 0.