Properties of Rank of a matrix: The rank (R) of a null or zero matrix is always zero. The rank (R) of a non-zero matrix is always non–zero value.The zero matrix is the only matrix whose rank is 0.Definition 11.5. 12 For a matrix A, the number of non-zero rows in E(A) is the rank of A, written r(A). For example, the matrix A of Example 11.5. 7 has two non-zero rows and so r(A) = 2.
How to write a 0 matrix : A zero matrix is a matrix with all its entries equal to zero. It is denoted by 'O' that can be expressed with a subscript to represent the dimension of the matrix.
What is non-zero in matrix
A nonzero matrix is a matrix that contains at least one non-zero element. In other words, it is a matrix that has a value other than zero in at least one of its entries. For example, the matrix. Copy code1 0 0 0 0 0 0 0 3.
Which matrix has no rank : A matrix is said to be rank-deficient if it does not have full rank. The rank deficiency of a matrix is the difference between the lesser of the number of rows and columns, and the rank.
The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 . If the determinant is nonzero, then the rank of the original matrix is equal to the number of rows/columns of the submatrix.
Can the rank of a matrix be defined as being the number of non zero eigenvalues of the matrix
The rank of any square matrix equals the number of nonzero eigen- values (with repetitions), so the number of nonzero singular values of A equals the rank of AT A. By a previous homework problem, AT A and A have the same kernel. It then follows from the “rank-nullity” theorem that AT A and A have the same rank.Well, one could say even more about the 0 x 0 matrix: Yes, it operates on the zero vector space (which contains only one single element = 0). So, it maps 0 to 0 since there is no other possible image. Hence, it must be the identity mapping on the zero space, and therefore, it is its own inverse.A nonzero matrix is a matrix that has at least one nonzero element. A nonzero vector is a vector with magnitude not equal to zero. : being, having, or involving a value other than zero.
Can the product of two nonzero matrices be zero : The product of two non-zero matrices can never be zero matrix.
Does every matrix have a rank : No. An n×n n × n matrix has rank n if and only if all of its rows are linearly independent. A matrix in which every row is all 1's will only have rank one. Try reducing the matrix to row echelon forms.
Can a non-square matrix have a rank
Thus, a non-singular matrix is also known as a full rank matrix. For a non-square [A] of m × n, where m > n, full rank means only n columns are independent. There are many other ways to describe the rank of a matrix. A matrix is said to be of rank zero when all of its elements become zero. The rank of the matrix is the dimension of the vector space obtained by its columns. The rank of a matrix cannot exceed more than the number of its rows or columns. The rank of the null matrix is zero.For most items, a sales rank of zero simply means that the item has never sold, or has not sold in a long, long, long time. This will apply to most of the items that have no sales rank, but there are sometimes exceptions. Some categories don't offer up sales ranks for all items. Electronics is an example.
What does it mean if a matrix has a non-zero determinant : invertible
In particular, the determinant is nonzero if and only if the matrix is invertible and the corresponding linear map is an isomorphism. The determinant of a product of matrices is the product of their determinants.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Can a non-zero matrix have rank zero? Weitere Antworten – Can the rank of a non-zero matrix be zero
Properties of Rank of a matrix: The rank (R) of a null or zero matrix is always zero. The rank (R) of a non-zero matrix is always non–zero value.The zero matrix is the only matrix whose rank is 0.Definition 11.5. 12 For a matrix A, the number of non-zero rows in E(A) is the rank of A, written r(A). For example, the matrix A of Example 11.5. 7 has two non-zero rows and so r(A) = 2.
How to write a 0 matrix : A zero matrix is a matrix with all its entries equal to zero. It is denoted by 'O' that can be expressed with a subscript to represent the dimension of the matrix.
What is non-zero in matrix
A nonzero matrix is a matrix that contains at least one non-zero element. In other words, it is a matrix that has a value other than zero in at least one of its entries. For example, the matrix. Copy code1 0 0 0 0 0 0 0 3.
Which matrix has no rank : A matrix is said to be rank-deficient if it does not have full rank. The rank deficiency of a matrix is the difference between the lesser of the number of rows and columns, and the rank.
The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 .
If the determinant is nonzero, then the rank of the original matrix is equal to the number of rows/columns of the submatrix.
Can the rank of a matrix be defined as being the number of non zero eigenvalues of the matrix
The rank of any square matrix equals the number of nonzero eigen- values (with repetitions), so the number of nonzero singular values of A equals the rank of AT A. By a previous homework problem, AT A and A have the same kernel. It then follows from the “rank-nullity” theorem that AT A and A have the same rank.Well, one could say even more about the 0 x 0 matrix: Yes, it operates on the zero vector space (which contains only one single element = 0). So, it maps 0 to 0 since there is no other possible image. Hence, it must be the identity mapping on the zero space, and therefore, it is its own inverse.A nonzero matrix is a matrix that has at least one nonzero element. A nonzero vector is a vector with magnitude not equal to zero.
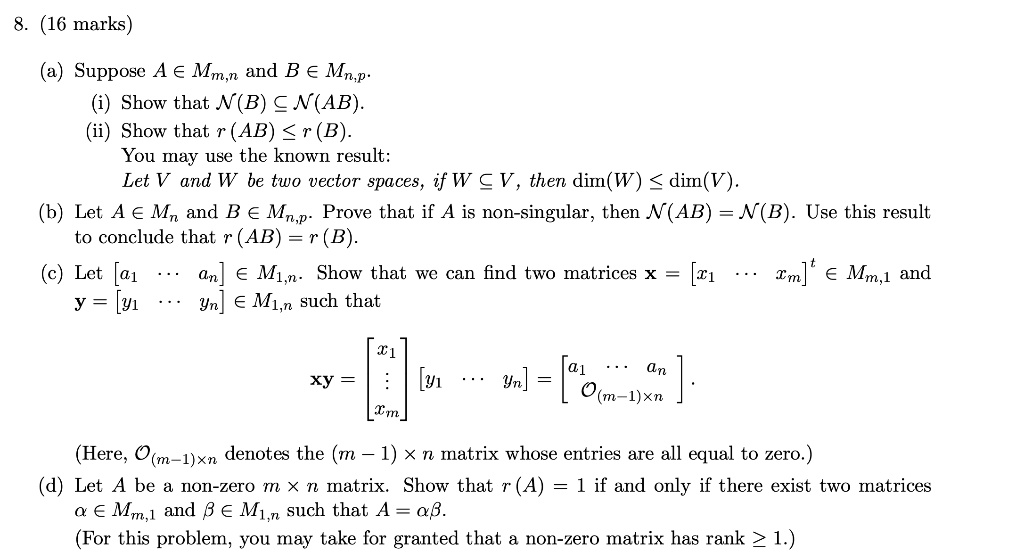
: being, having, or involving a value other than zero.
Can the product of two nonzero matrices be zero : The product of two non-zero matrices can never be zero matrix.
Does every matrix have a rank : No. An n×n n × n matrix has rank n if and only if all of its rows are linearly independent. A matrix in which every row is all 1's will only have rank one. Try reducing the matrix to row echelon forms.
Can a non-square matrix have a rank
Thus, a non-singular matrix is also known as a full rank matrix. For a non-square [A] of m × n, where m > n, full rank means only n columns are independent. There are many other ways to describe the rank of a matrix.
A matrix is said to be of rank zero when all of its elements become zero. The rank of the matrix is the dimension of the vector space obtained by its columns. The rank of a matrix cannot exceed more than the number of its rows or columns. The rank of the null matrix is zero.For most items, a sales rank of zero simply means that the item has never sold, or has not sold in a long, long, long time. This will apply to most of the items that have no sales rank, but there are sometimes exceptions. Some categories don't offer up sales ranks for all items. Electronics is an example.
What does it mean if a matrix has a non-zero determinant : invertible
In particular, the determinant is nonzero if and only if the matrix is invertible and the corresponding linear map is an isomorphism. The determinant of a product of matrices is the product of their determinants.