If the determinant is zero, the matrix is inconsistent and has either no solutions or infinitely many solutions depending on the specific values in the matrix.The rank of a matrix is equivalent to the number of pivots of the matrix. The sum of the number of pivots and free variables equals to the dimension of the matrix. In other words, the number of free variables = dimension of a matrix minus the rank.If a matrix is a square matrix and all of its columns are linearly independent, then the matrix equation has a unique solution .
What is the Gauss-Jordan elimination method : Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix: Swap the positions of two of the rows. Multiply one of the rows by a nonzero scalar.
Can a leading entry be 0
The leading entry in a row of a matrix is the first non-zero entry in that row, starting from the left. Of course, if a row is all zeroes then it doesn't have a leading entry.
Is A zero matrix empty : By the way, the null matrix or zero matrix is not called the “empty matrix”. Arguably, the only thing that could be called an “empty matrix” is one with no entries (just as the empty set has no elements) — which is possible only if its dimension is n×0 n × 0 or 0×n 0 × n (a non-standard definition).
The column space of A is R1. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1. 1 4 5 A = 2 8 10 2 Page 3 has rank 1 because each of its columns is a multiple of the first column. No. An n×n n × n matrix has rank n if and only if all of its rows are linearly independent. A matrix in which every row is all 1's will only have rank one. Try reducing the matrix to row echelon forms.
What is the rank of a matrix
The rank of the matrix refers to the number of linearly independent rows or columns in the matrix. ρ(A) is used to denote the rank of matrix A. A matrix is said to be of rank zero when all of its elements become zero. The rank of the matrix is the dimension of the vector space obtained by its columns.If we have any row where all entries are 0 except for the entry in the last column, then the system implies 0=1. More succinctly, if we have a leading 1 in the last column of an augmented matrix, then the linear system has no solution.You can perform three operations on matrices in order to eliminate variables in a system of linear equations:
You can multiply any row by a constant (other than zero). multiplies row three by –2 to give you a new row three.
You can switch any two rows. swaps rows one and two.
You can add two rows together.
Yes, Gaussian elimination always works for solving systems of linear equations, given that the system has a unique solution. However, if the system has no solution or an infinite number of solutions, Gaussian elimination will not provide a unique solution.
What does rank a 0 implies : The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 .
Is 0 matrix rref : Is [0000] [ 0 0 0 0 ] in reduced row echelon form Short answer: Yes. A zero matrix is row-equivalent only to itself, therefore it must be its own RREF. Longer answer: row echelon form is just a statement about where the leading entries can be (i.e. the first nonzero entry in each row).
Can you have a 0 by 0 matrix
Well, one could say even more about the 0 x 0 matrix: Yes, it operates on the zero vector space (which contains only one single element = 0). So, it maps 0 to 0 since there is no other possible image. Hence, it must be the identity mapping on the zero space, and therefore, it is its own inverse. Zero is an important number, even though it represents a quantity of nothing! To summarize: Zero is a number between negative numbers and positive numbers. It is necessary as a placeholder in whole numbers and decimal numbers. It represents a place with no amount or null value.Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
Which matrix has no rank : A matrix is said to be rank-deficient if it does not have full rank. The rank deficiency of a matrix is the difference between the lesser of the number of rows and columns, and the rank.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Can a matrix have rank 0? Weitere Antworten – Is the zero matrix consistent
If the determinant is zero, the matrix is inconsistent and has either no solutions or infinitely many solutions depending on the specific values in the matrix.The rank of a matrix is equivalent to the number of pivots of the matrix. The sum of the number of pivots and free variables equals to the dimension of the matrix. In other words, the number of free variables = dimension of a matrix minus the rank.If a matrix is a square matrix and all of its columns are linearly independent, then the matrix equation has a unique solution .
What is the Gauss-Jordan elimination method : Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix: Swap the positions of two of the rows. Multiply one of the rows by a nonzero scalar.
Can a leading entry be 0
The leading entry in a row of a matrix is the first non-zero entry in that row, starting from the left. Of course, if a row is all zeroes then it doesn't have a leading entry.
Is A zero matrix empty : By the way, the null matrix or zero matrix is not called the “empty matrix”. Arguably, the only thing that could be called an “empty matrix” is one with no entries (just as the empty set has no elements) — which is possible only if its dimension is n×0 n × 0 or 0×n 0 × n (a non-standard definition).
The column space of A is R1. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1. 1 4 5 A = 2 8 10 2 Page 3 has rank 1 because each of its columns is a multiple of the first column.
No. An n×n n × n matrix has rank n if and only if all of its rows are linearly independent. A matrix in which every row is all 1's will only have rank one. Try reducing the matrix to row echelon forms.
What is the rank of a matrix
The rank of the matrix refers to the number of linearly independent rows or columns in the matrix. ρ(A) is used to denote the rank of matrix A. A matrix is said to be of rank zero when all of its elements become zero. The rank of the matrix is the dimension of the vector space obtained by its columns.If we have any row where all entries are 0 except for the entry in the last column, then the system implies 0=1. More succinctly, if we have a leading 1 in the last column of an augmented matrix, then the linear system has no solution.You can perform three operations on matrices in order to eliminate variables in a system of linear equations:
Yes, Gaussian elimination always works for solving systems of linear equations, given that the system has a unique solution. However, if the system has no solution or an infinite number of solutions, Gaussian elimination will not provide a unique solution.
What does rank a 0 implies : The rank of A is the dimension of its column space C(A)⊆Rn C ( A ) ⊆ R n . The only vector subspace of Rn with zero dimension is the trivial space {0n} , where 0n is the n -dimensional zero vector. Hence, A is of rank zero if and only if it is the zero matrix, that is, if and only if all elements of A are 0 .
Is 0 matrix rref : Is [0000] [ 0 0 0 0 ] in reduced row echelon form Short answer: Yes. A zero matrix is row-equivalent only to itself, therefore it must be its own RREF. Longer answer: row echelon form is just a statement about where the leading entries can be (i.e. the first nonzero entry in each row).
Can you have a 0 by 0 matrix
Well, one could say even more about the 0 x 0 matrix: Yes, it operates on the zero vector space (which contains only one single element = 0). So, it maps 0 to 0 since there is no other possible image. Hence, it must be the identity mapping on the zero space, and therefore, it is its own inverse.
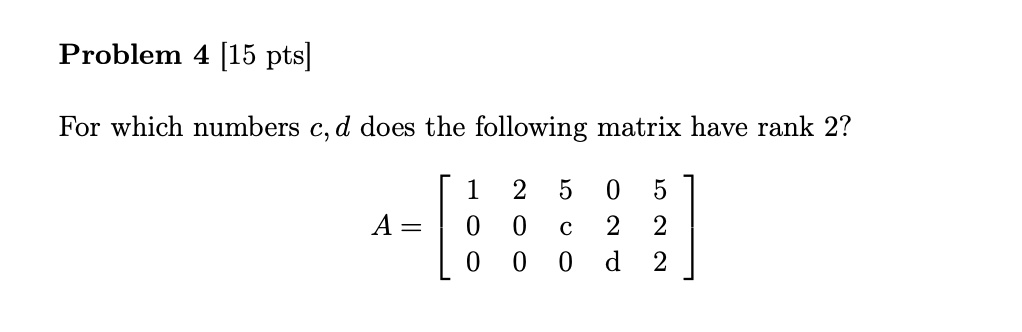
Zero is an important number, even though it represents a quantity of nothing! To summarize: Zero is a number between negative numbers and positive numbers. It is necessary as a placeholder in whole numbers and decimal numbers. It represents a place with no amount or null value.Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with rank equal to one. Such matrices are also called dyads.
Which matrix has no rank : A matrix is said to be rank-deficient if it does not have full rank. The rank deficiency of a matrix is the difference between the lesser of the number of rows and columns, and the rank.