A matrix having at least one dimension equal to zero is called an empty matrix. The simplest empty matrix is 0-by-0 in size. Examples of more complex matrices are those of dimension 0 -by- 5 or 10 -by- 0 -by- 20.A zero matrix is a matrix that has all its elements equal to zero. Since a zero matrix contains only zeros as its elements, therefore, it is also called a null matrix.Just as any number multiplied by zero is zero, there is a zero matrix such that any matrix multiplied by it results in that zero matrix.
Is a zero matrix having all elements are zero True or false : A null (zero) matrix is a matrix in which all elements are zero.
Is A zero matrix empty
By the way, the null matrix or zero matrix is not called the “empty matrix”. Arguably, the only thing that could be called an “empty matrix” is one with no entries (just as the empty set has no elements) — which is possible only if its dimension is n×0 n × 0 or 0×n 0 × n (a non-standard definition).
Does 1 1 matrix exist : Yes! A 1×n matrix is a row representation of an n-vector, and its column representation is an n×1 matrix. Matrix multiplication of a row n-vector by a column n-vector gives a 1×1 matrix which represents the inner product of the two n-vectors.
If you multiply a matrix by any zero matrix, you get another zero matrix.
The zero matrix also represents the linear transformation which sends all the vectors to the zero vector. It is idempotent, meaning that when it is multiplied by itself, the result is itself. The zero matrix is the only matrix whose rank is 0.
Can all eigenvalues be 0
Conversely, if the eigenvalues of a square matrix are all zero, then is nilpotent. Clearly, if A q = 0 for some positive integer , then all eigenvalues of are zero; if has at least one eigenvalue which is nonzero, then A k ≠ 0 for all k ∈ Z ⩾ 0 .Zero is an important number, even though it represents a quantity of nothing! To summarize: Zero is a number between negative numbers and positive numbers. It is necessary as a placeholder in whole numbers and decimal numbers. It represents a place with no amount or null value.The eigenvalues or the zero matrix are all 0 so, yes, the zero matrix is positive semi-definite. And, as Gary Moon said, it is also negative semi-definite.
In all videos, vectors are represented as 2×1 matrices and transformation to a vector is represented as either 2×2 or 2×1 (if transforming to a number line) matrices.
Can a number be a matrix : Yes, a number can be thought of as 1×1 matrix. Note that for a general matrix M (over, say, the real numbers) and a real number a, the notation a.
Is a zero matrix diagonalizable : However, there is an important class of matrices of which none except the zero matrix is diagonalisable (see below).
Is 0 times a matrix 0
Summary: Comparing the zero matrix to the real number zero
In the investigations above, we saw that a zero matrix behaves much like the real number zero. Any number times zero is zero. (e.g a ⋅ 0 = 0 ).
Zero matrices can be of any size, whether square or rectangular, and are denoted by a boldface zero or sometimes by the symbol O.So if A is invertible, there is no nontrivial solution to A→x=→0, and hence 0 is not an eigenvalue of A. If A is not invertible, then there is a nontrivial solution to A→x=→0, and hence 0 is an eigenvalue of A. This leads us to our final addition to the Invertible Matrix Theorem.
Why can’t 0 be an eigenvector : We do not consider the zero vector to be an eigenvector: since A0=0=λ0 for every scalar λ, the associated eigenvalue would be undefined.
![Kladsko-5-malý-Karlův-Most[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Kladsko-5-maly-Karluv-Most1-1024x692-250x120.jpg)
![Stubai[1]](https://www.einarstrayorchestra.com/wp-content/uploads/2024/06/Stubai1-250x120.jpg)
Antwort Does a zero matrix exist? Weitere Antworten – Is there an empty matrix
Empty Matrices
A matrix having at least one dimension equal to zero is called an empty matrix. The simplest empty matrix is 0-by-0 in size. Examples of more complex matrices are those of dimension 0 -by- 5 or 10 -by- 0 -by- 20.A zero matrix is a matrix that has all its elements equal to zero. Since a zero matrix contains only zeros as its elements, therefore, it is also called a null matrix.Just as any number multiplied by zero is zero, there is a zero matrix such that any matrix multiplied by it results in that zero matrix.
Is a zero matrix having all elements are zero True or false : A null (zero) matrix is a matrix in which all elements are zero.
Is A zero matrix empty
By the way, the null matrix or zero matrix is not called the “empty matrix”. Arguably, the only thing that could be called an “empty matrix” is one with no entries (just as the empty set has no elements) — which is possible only if its dimension is n×0 n × 0 or 0×n 0 × n (a non-standard definition).
Does 1 1 matrix exist : Yes! A 1×n matrix is a row representation of an n-vector, and its column representation is an n×1 matrix. Matrix multiplication of a row n-vector by a column n-vector gives a 1×1 matrix which represents the inner product of the two n-vectors.
If you multiply a matrix by any zero matrix, you get another zero matrix.
The zero matrix also represents the linear transformation which sends all the vectors to the zero vector. It is idempotent, meaning that when it is multiplied by itself, the result is itself. The zero matrix is the only matrix whose rank is 0.
Can all eigenvalues be 0
Conversely, if the eigenvalues of a square matrix are all zero, then is nilpotent. Clearly, if A q = 0 for some positive integer , then all eigenvalues of are zero; if has at least one eigenvalue which is nonzero, then A k ≠ 0 for all k ∈ Z ⩾ 0 .Zero is an important number, even though it represents a quantity of nothing! To summarize: Zero is a number between negative numbers and positive numbers. It is necessary as a placeholder in whole numbers and decimal numbers. It represents a place with no amount or null value.The eigenvalues or the zero matrix are all 0 so, yes, the zero matrix is positive semi-definite. And, as Gary Moon said, it is also negative semi-definite.
In all videos, vectors are represented as 2×1 matrices and transformation to a vector is represented as either 2×2 or 2×1 (if transforming to a number line) matrices.
Can a number be a matrix : Yes, a number can be thought of as 1×1 matrix. Note that for a general matrix M (over, say, the real numbers) and a real number a, the notation a.
Is a zero matrix diagonalizable : However, there is an important class of matrices of which none except the zero matrix is diagonalisable (see below).
Is 0 times a matrix 0
Summary: Comparing the zero matrix to the real number zero
In the investigations above, we saw that a zero matrix behaves much like the real number zero. Any number times zero is zero. (e.g a ⋅ 0 = 0 ).
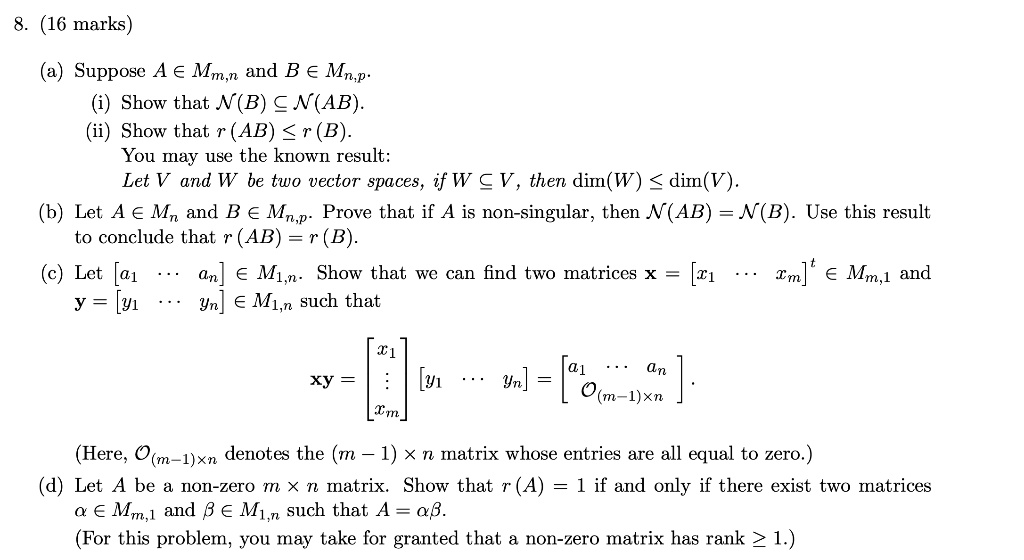
Zero matrices can be of any size, whether square or rectangular, and are denoted by a boldface zero or sometimes by the symbol O.So if A is invertible, there is no nontrivial solution to A→x=→0, and hence 0 is not an eigenvalue of A. If A is not invertible, then there is a nontrivial solution to A→x=→0, and hence 0 is an eigenvalue of A. This leads us to our final addition to the Invertible Matrix Theorem.
Why can’t 0 be an eigenvector : We do not consider the zero vector to be an eigenvector: since A0=0=λ0 for every scalar λ, the associated eigenvalue would be undefined.